1.二叉排序树的定义

二叉排序树，又称二叉查找树（BST，Binary Search Tree)
默认不允许两个结点的关键字相同。

1.二叉排序树的性质:

任意一棵二叉排序树的子树的结点大小都满足“左小右大”。

左子树上所有结点的关键字均小于根结点的关键字。
右子树上所有结点的关键字均大于根结点的关键字。
左子树和右子树又各是一棵二叉排序树。

例如下面这棵二叉排序树：
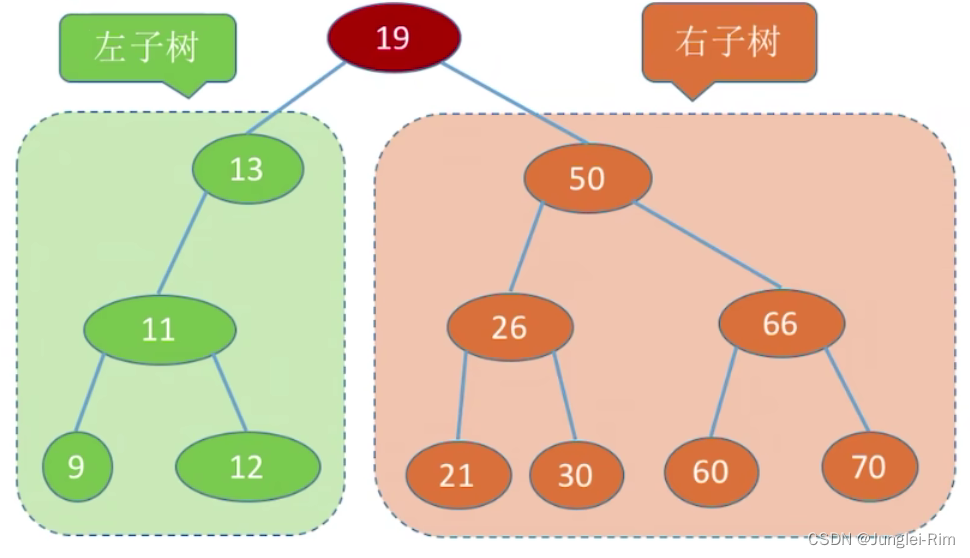
在这里插入图片描述

2.二叉排序树的特点：

左子树结点值<根结点值<右子树结点值。
进行中序遍历，可以得到一个递增的有序序列。
二叉排序树可用于元素的有序组织、搜索。

2.查找操作

从根节点开始，目标值更小往左找，目标值更大往右找。
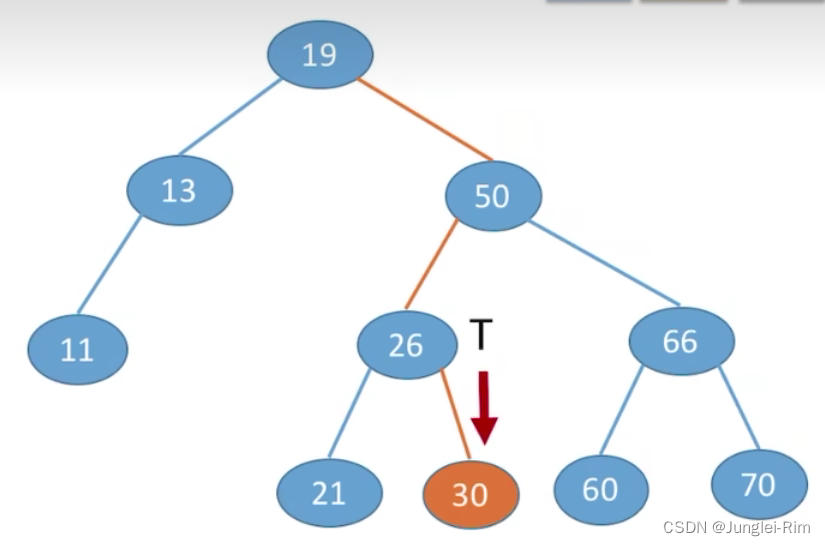
在这里插入图片描述

根据二叉排序树的特点：左子树结点值<根结点值<右子树结点值

1.查找步骤：

若树非空，目标值与根结点的值比较:
若相等，则查找成功;
若小于根结点，则在左子树上查找，否则在右子树上查找。
查找成功，返回结点指针;
查找失败返回NULL.

2.代码实现

1.二叉排序树结点设计：

//二叉排序树结点
typedef struct BSTNode {
    int key;
    struct BSTNode *lchild, *rchild;
} BSTNode, *BSTree;

2.查找函数设计：
非递归的实现：
最坏空间复杂度为O（1）

//在二叉排序树中查找值为key 的结点
BSTNode *BST_Search(BSTree T,int key){
    while(T!=NULL&&key !=T->key) {//若树空或等于根结点值,则结束循环
        if( key<T->key) T=T->lchild;//小于，则在左子树上查找
        else T=T->rchild;//大于，则在右子树上查找
    }
    return T;
}

递归实现：
最坏空间复杂度为O（h）

//在二叉排序树中查找值为key 的结点（递归实现)
BSTNode *BSTSearch(BSTree T, int key) {
    if (T == NULL)
        return NULL;//查找失败
    if (key == T->key)
        return T;//查找成功
    else if (key < T->key)
        return BSTSearch(T->lchild, key);//在左子树中找
    else
        return BSTSearch(T->rchild, key);//在右子树中找
}

3.插入操作

找到应该插入的位置（一定是叶子结点)，一定要注意修改其父节点指针。

1.实现步骤：

若原二叉排序树为空，则直接插入结点;
否则，若关键字k小于根结点值，则插入到左子树，
若关键字k大于根结点值，则插入到右子树

2.代码实现（递归插入）

最坏空间复杂度为O（h）

//在二叉排序树插入关键字为k的新结点（递归实现)
int BST_Insert(BSTree &T, int k) {
    if (T == NULL) {//原树为空，新插入的结点为根结点
        T = (BSTree) malloc(sizeof(BSTNode));
        T->key = k;
        T->lchild = T->rchild = NULL;
        return 1;//返回1，插入成功
    } else if (k == T->key)//树中存在相同关键字的结点，插入失败
        return 0;
    else if (k < T->key)//插入到T的左子树
        return BST_Insert(T->lchild, k);
    else//插入到T的右子树
        return BST_Insert(T->rchild, k);
}

3.通过插入操作构造一棵二叉排序树

//按照str[] 中的关键字序列建立二叉排序树
void Creat_BST(BSTree &T, int str[], int n) {
    T = NULL;//初始时T为空树
    int i = 0;
    while (i < n) {//依次将每个关键字插入到二叉排序树中
        BST_Insert(T, str[i]);
        i++;
    }
}

给定不同的关键字序列可能得到同款二叉排序树，也可能得到不同款二叉排序树。

4.删除操作

1.实现步骤：

先搜索找到目标结点
若被删除结点z是叶结点，则直接删除，不会破坏二叉排序树的性质。
若结点z只有一棵左子树或右子树，则让z的子树成为z父结点的子树，替代z的位置。
若结点z有左、右两棵子树，则令z的直接后继（或直接前驱）替代z，然后从二叉排序树中删去这个直接后继（或直接前驱），这样就转换成了第一或第二种情况。（采用的是中序遍历）
z的直接后继:z的右子树中最左下结点（该节点一定没有左子树)
z的直接前驱:z的左子树中最右下结点（该节点一定没有右子树)