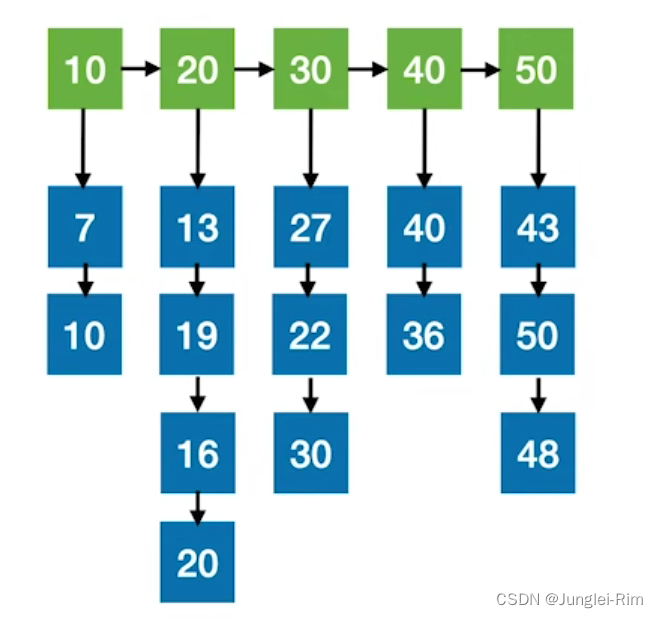
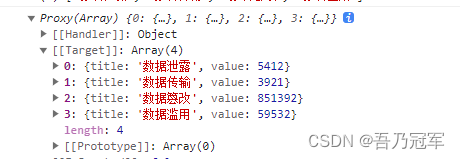
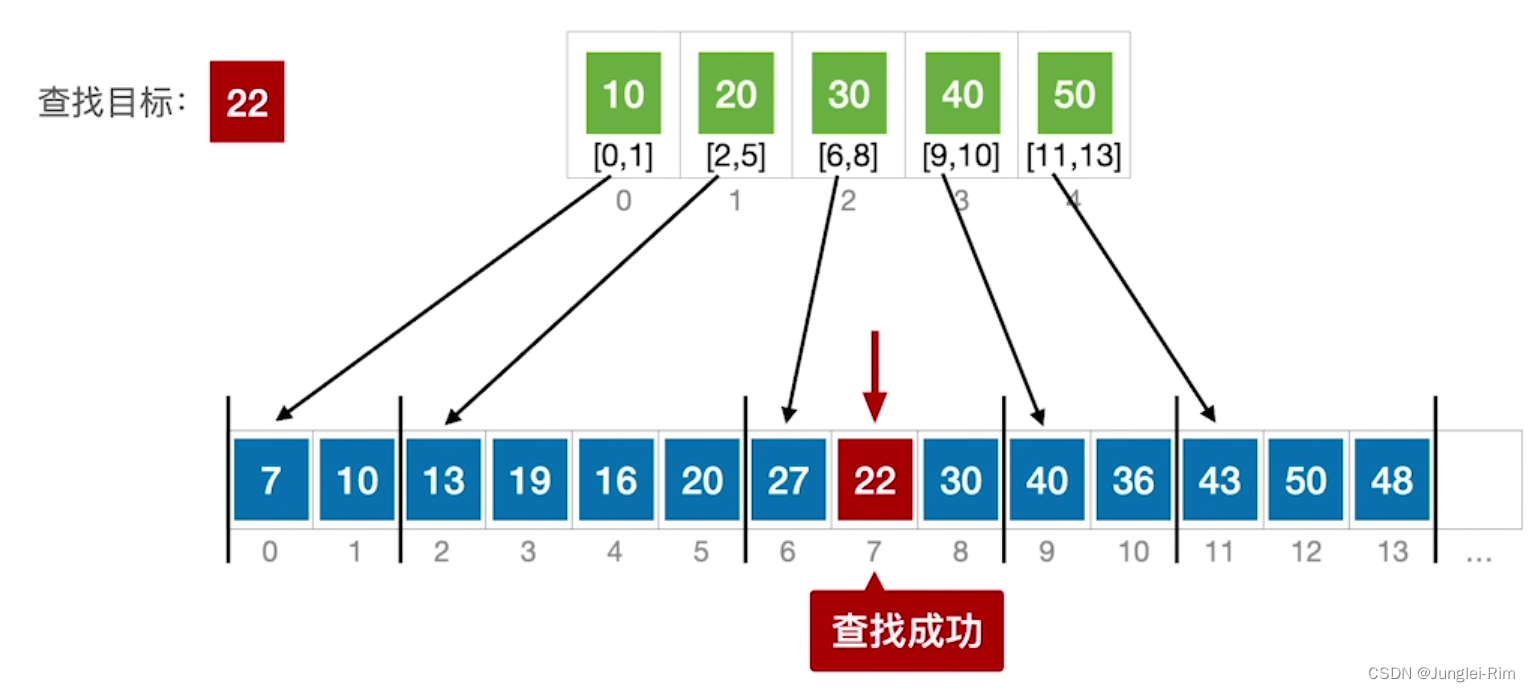
数据分块存储,分块查找特点:块内无序、块间有序。

1.分块查找的算法思想

1.使用顺序查找查索引

设置一个索引表，
索引表数据结构设计：

//索引表
typedef struct {
    ElemType maxValue;
    int low,high;
}Index;

//顺序表存储实际元素
ElemType List[100] ;

分块查找，又称索引顺序查找，算法过程如下:

1. “索引表”中保存每个分块的最大关键字和分块的存储区间。
2. 在索引表中确定待查记录所属的分块（可顺序、可折半)
3. 再在分块内进行顺序查找

2.使用折半查找查索引

• 若索引表中不包含目标关键字，则折半查找索引表最终停在low>high，要在low所指分块中查找。
• 原因:最终low左边一定小于目标关键字，high右边一定大于目标关键字。而分块存储的索引表中保存的是各个分块的最大关键字。

2.查找效率分析（ASL）

ASL=查索引表的平均查找长度＋查分块的平均查找长度

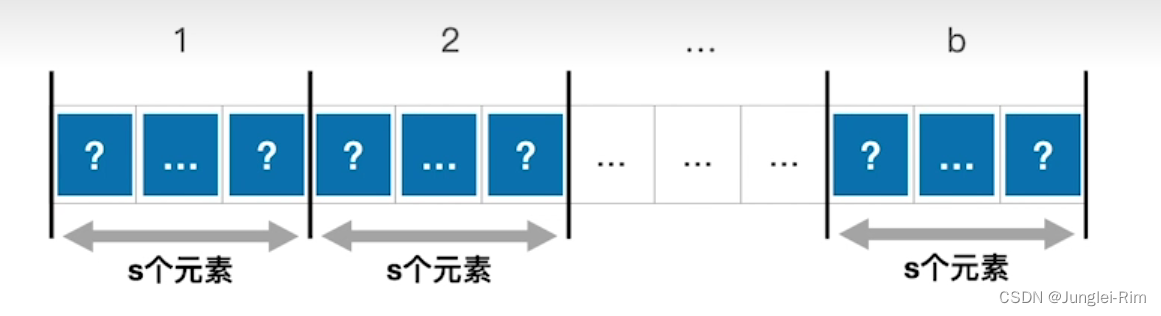
假设，长度为n的查找表被均匀地分为b块，每块s个元素。则$$n=sb$$

设索引查找和块内查找的平均查找长度分别为L1、Ls，则分块查找的平均查找长度为$$ASL=L1+Ls$$

1.采用顺序查找查索引表

则索引查找的长度为：$$L1=\frac{b+1}{2}$$块内查找长度为：$$Ls=\frac{s+1}{2}$$则分块查找的平均查找长度为：$$ASL=\frac{s^2+2s+n}{2s}$$

当s = $\sqrt{n}$时，ASL最小为：$\sqrt{n}+1$.

2.折半查找查索引表

则 $$L1=lo{g}_2(b+1)$$, $$Ls=\frac{s+1}{2}$$,$$ASL=[lo{g}_2(b+1)]+\frac{s+1}{2}$$

若查找表是“动态查找表”,则采用链式存储存放元素。