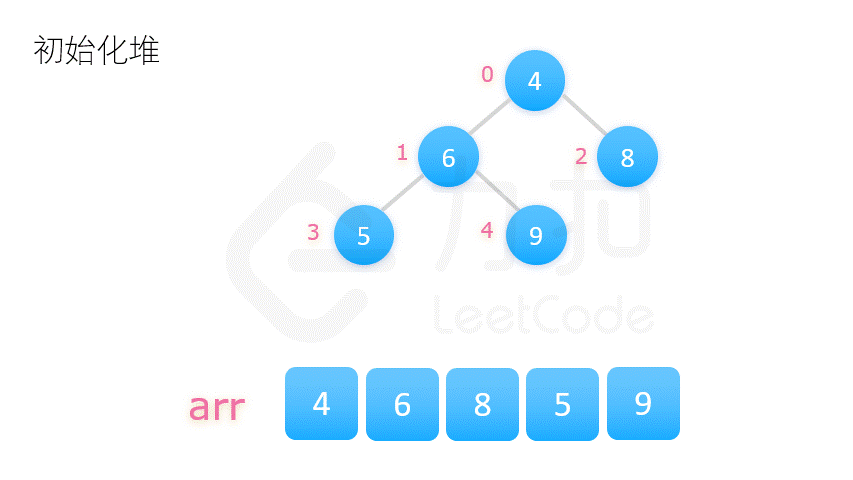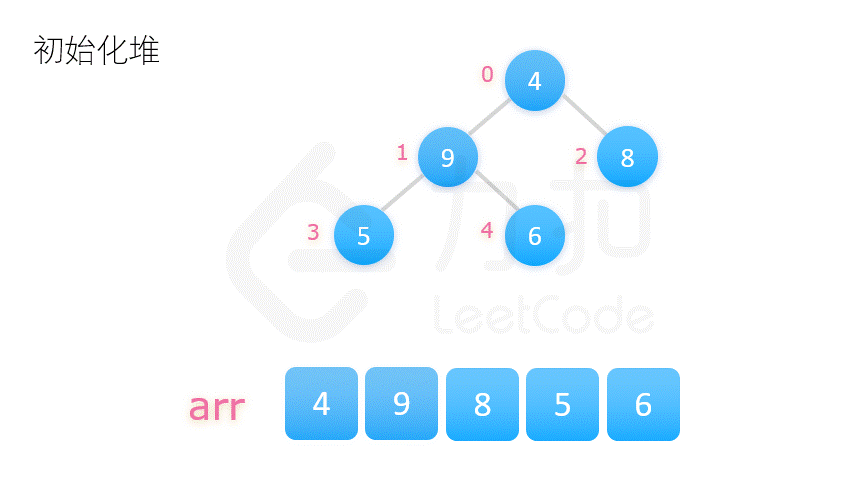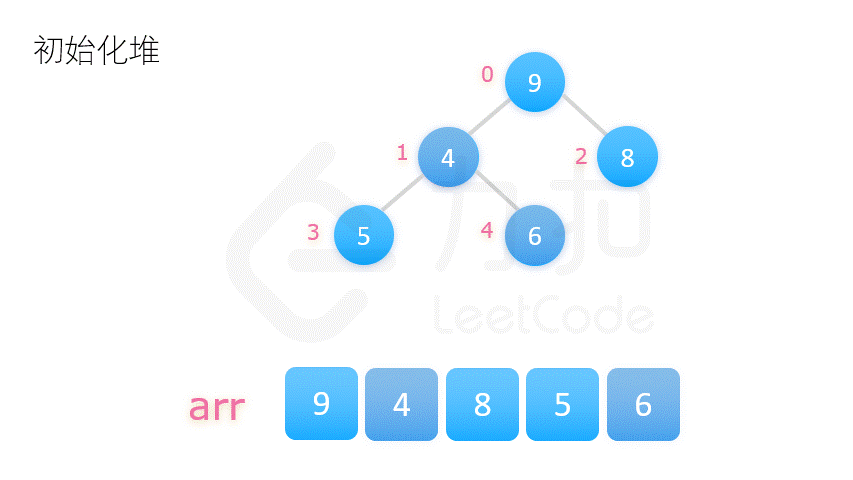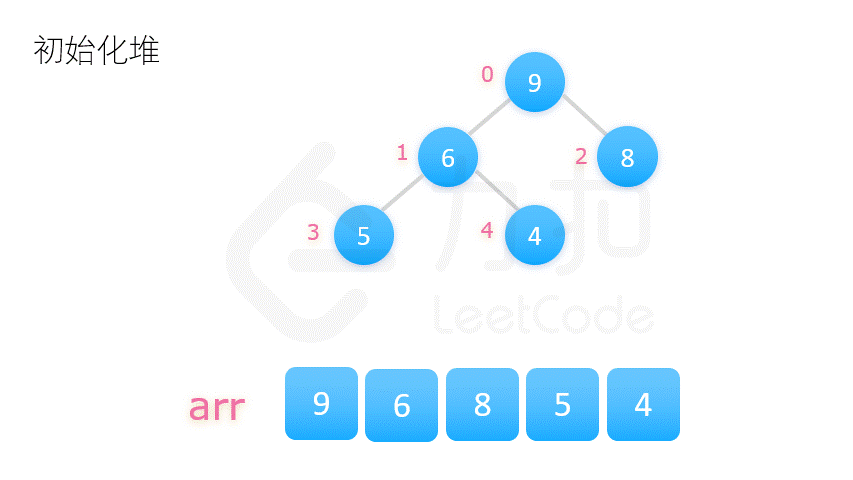
堆排序过程如下：
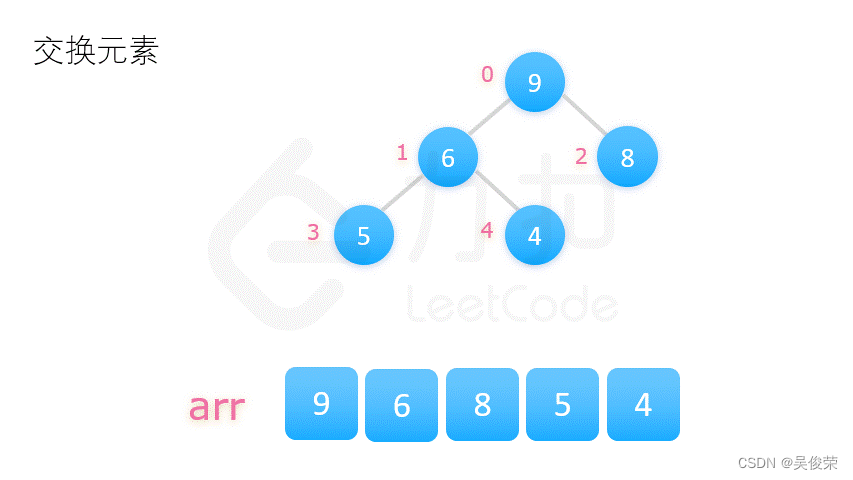
1.用数列构建出一个大顶堆，取出堆顶的数字；
2.调整剩余的数字，构建出新的大顶堆，再次取出堆顶的数字；
3.循环往复，完成整个排序。

构建大顶堆有两种方式：
1.从 0 开始，将每个数字依次插入堆中，一边插入，一边调整堆的结构，使其满足大顶堆的要求；
2.将整个数列的初始状态视作一棵完全二叉树，自底向上调整树的结构，使其满足大顶堆的要求。
二更为常用

void swap(vector<int> arr, int i, int j)
{
    int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;

}

// 调整大顶堆，第三个参数表示剩余未排序的数字的数量，也就是剩余堆的大小
 void maxHeapify(vector<int> arr, int i, int heapSize) {
    // 左子结点下标
    int l = 2 * i + 1;
    // 右子结点下标
    int r = l + 1;
    // 记录根结点、左子树结点、右子树结点三者中的最大值下标
    int largest = i;
    // 与左子树结点比较
    if (l < heapSize && arr[l] > arr[largest]) {
        largest = l;
    }
    // 与右子树结点比较
    if (r < heapSize && arr[r] > arr[largest]) {
        largest = r;
    }
    if (largest != i) {
        // 将最大值交换为根结点
        swap(arr, i, largest);
        // 再次调整交换数字后的大顶堆
        maxHeapify(arr, largest, heapSize);
    }
}

// 构建初始大顶堆
void buildMaxHeap(vector<int> arr) {
    // 从最后一个非叶子结点开始调整大顶堆，最后一个非叶子结点的下标就是 arr.length / 2-1
    for (int i = arr.size() / 2 - 1; i >= 0; i--) {
        maxHeapify(arr, i, arr.size());
    }
}

void heapSort(vector<int> arr) {
    // 构建初始大顶堆
    buildMaxHeap(arr);
    for (int i = arr.size() - 1; i > 0; i--) {
        // 将最大值交换到数组最后
        swap(arr, 0, i);
        // 调整剩余数组，使其满足大顶堆
        maxHeapify(arr, 0, i);
    }
}