在APS系统设计中,根据不同的业务场景,会出现两种截然相反的策略需求,分别是(资源)负载均衡与成本最优(最低),两种策略分别适用于不同的业务场景。本文我们将这两种策略的适用场景、方案原理作初步探讨,并就这些策略在OptaPlanner中的实现思路稍作分析。事实上,这两种策略不仅仅在APS自动生成生产计划的逻辑中存在,在较高层次的主生产计划(MPS)、对具体设备加工机台的实时生产调度指挥模块,乃至物流运输中的VRP(车辆路径规划)场景中,均会出现,基本原理下实现方式则大同小异。
业务场景
在定制生产计划过程中,对计划的要求,除了需要符合一些“硬性要求”外,还会针对一个或多个特定目标尽可能迫近。其中硬性要求部分将在本文最后的【硬约束与软约束】小节中详述。对于特定目标,可以理解为制定计划的最终要求,也是一个生产计划优劣的关键所在,我们称之为排程策略。
在某些行业中生产旺季出现订单需求大于产能时,订单的准交率是一个重要的KPI,在这种情况下,实现订单的准时交付比节约成本来得更重要,此时制定计划过程中生产加工的作业效率优先是一个关键要求,在确保优先使用高效率设备的前提下,各设备的任务安排尽可能均衡,从而更大程度上提升设备利用率,缩短任务的加工周期,从而减少订单延误、提高准交率。此时使用APS进行自动计划时,设定资源均衡策略,能很好地实现这一目标。
相反,当行业处于淡季时订单量减少,交付压力也随之减少。在确保订单不延误的前提下,降低成本则成了首要目标。在定制计划过程中,尽可能使用低成本资源,则是降本的其中一个重要手段。例如尽可能使用低成本的机台、低时薪的人员,尽可能使用少的设备完成指定作业任务等。此时,使用APS系统时,通过选择成本优先策略,能在确保符合其它要求(例如工艺、质量要求)要求的前提下,尽可能降低成本。
两种策略的实现原理
环境条件
假设有以下任务要求与可用设备,见下表:
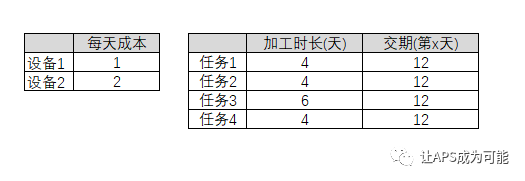
即简化后的规划数据集(待排数量)中存在以下信息:
-
存在2台设备,设备1每天开机运行成本是1(即单位成本是1),设备2每天的运行成本是2.
-
存在4个任务,其中任务1、任务2、任务4的加工时长是4天,任务3的加工时长是6天;所有任务的交期均为第12天(以第1天的基准进行排程)。
方案1:资源负载均衡策略
若使用资源负载均衡策略,将会得出以下方案,其目标是所有设备获得的任务天数应该尽可能均等。通过下图可以观察到,设备2比设备1工作天数多2天。这种情况下所有设备的利用率是最高的,即所有设备尽可能并行开机,加快整体作业效率.
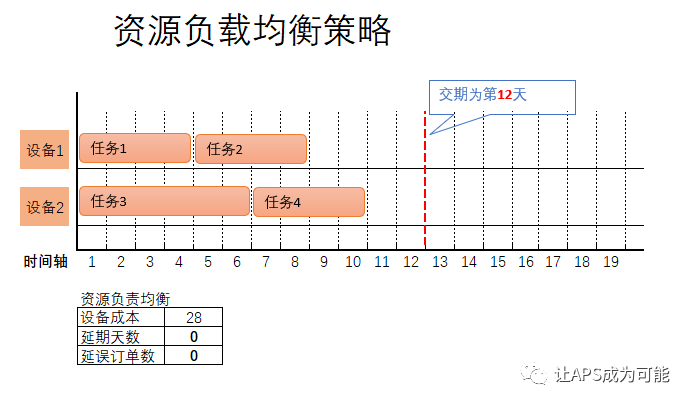
从方案的交付效率来看,最后一个任务(任务4)是第10天完成,距离交期仍有2天盈余。但成本(资源的占用成本)并非最优,该方案的资源成本(即设备成本)为28,分解计算如下:
-
设备1(单位成本为1),任务1(4天 * 1) + 任务1(4天 * 1) = 8
-
设备2(单位成本为2),任务3(6天 * 2) + 任务4(4天 * 2) = 20
-
得出所有任务对设备的占用成本为28.
小结:当使用资源负载均衡策略时,会得到一个各设备的任务分配尽可能平衡的方案,这种方案表现为资源利用率最高,但成本并不一定最优.
当处于生产旺季,因为订单多且复杂,对准交率要求高时,可以使用负载均衡策略。
方案2:资源成本优先策略
若将系统的排程策略设定为成本优先,引擎会在分配资源的任务时,遂行与方案1截然相反的策略偏好。如下两图(方案A与方案B),按该策略获得的方案中,为了降低设备使用成本,而在一定程度上放弃部分准交率。尽管基于降本策略,引擎仍会针对准交要求,作出限制范围内的优化。其中可能产生以下两个方案,引擎会基于准交要求,更智能地选择方案B.
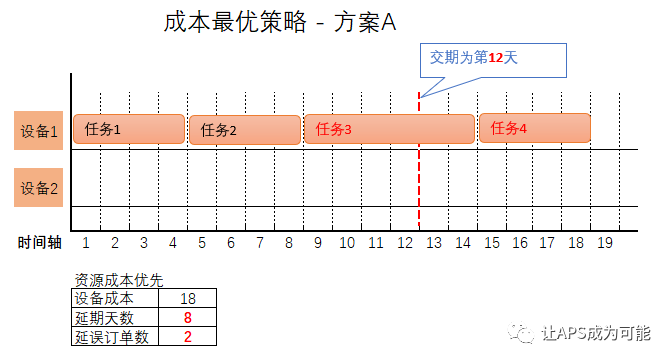
基于成本最优策略,有可能排出一个如上图的方案A. 该方案各项指标如下:
-
设备成本为18: 各任务均分布在设备1(4天 + 4天 + 6天 + 4天) * 1 = 18.
任务总延期天数为8天: 其中任务3延期2天(14-12), 任务4延期6天(18-12),共延误8天。
订单延误总数为2: 任务3、任务4同均延误。
该方案显然比较“鲁莽”,引擎会继续寻找更佳方案,有可能会找到满足成本最优要求,但准交率更佳的方案,如下图的方案B。
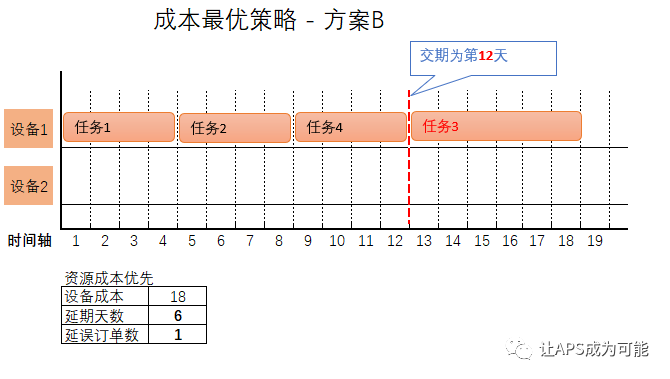
同样基于成本最优策略,引擎将尽可能找出如上图的方案B.该方案的各项指标如下:
-
设备成本为18: (4天 + 4天 + 6天 + 4天) * 1 = 18.
-
任务总延期天数为6天:任务4延期6天(18-12).
-
延误任务数为1: 仅任务4延误。
当处于生产淡季,成本控制作为重要KPI,且容许一定程度的延误,或生产延误的时间可通过其它环节(例如仓储与物流运输)节省回来时。可以设定为成本最优策略。成本最优策略执行过程中,引擎仍会基于其它指标,例如延误天数、延误订单数等进行优化,从而获得一个相对最优的成本优化计划方案。
小结:在确保成本最优(可牺牲交期)的策略设定下,将会出现一定程度的延误,但引擎仍会尽最大可能减少延误程度。而对于延误订单数与延误天数,则又可拆分出更多不同的诉求,进一步影响引擎的决策行为,本文不再展开。
方案3:保证交期的前提下执行成本优先策略
当我们处于保证交期不延误作为硬指标的要求场景下,可以基于“除非资源不足,否交期不得延误”的前提,生成一个成本最优方案,如下图
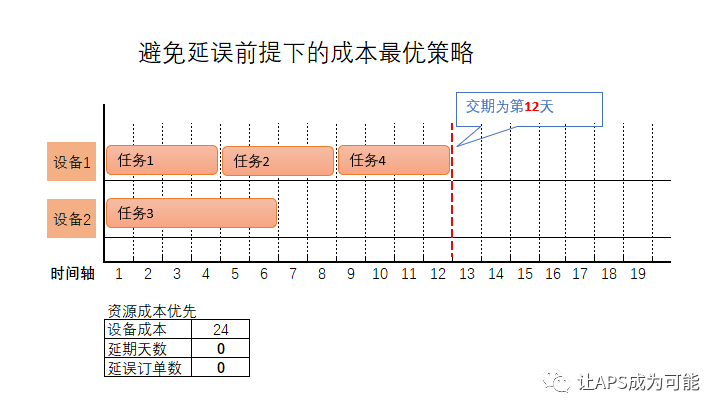
对于上图中避免延误的成本最优策略获得的方案,该方案的各项指标如下:
-
设备成本为24:设备1,(4天 * 3) * 1 = 12; 设备2,6天 * 2 = 12, 总成本为24.
-
延期天数与延误订单数均为0.
小结:在保证订单不延误的前提下,引擎可以寻找到一个满足条件,且占用资源尽可能少的方案。当数据集更大,反映的情况更复杂的情况下,人为排产将面临巨大挑战,大部分情况在,需要考虑的复杂远超人力可顾及的水平。
方案4:综合均衡与成本两种策略(需要去除量纲)
除了上述将资源成本与均衡分开考虑的情况,在实际排产工作中我们还会遇到对成本与均衡两个要求综合考虑的情况,这种情况将更为复杂。例如:“当延误小于一定的程度(例如延误天数、或延误订单量小于某个阈值)时,仅使用低成本设备。”,“每延误1天算作1分,某台设备成本10分,因此延误10天以下,不启用该设备”。
诸如此类情况,实际上是对于不同的因素作加权计算结合考虑,从而实现去除不同因素的量纲(例如延误按天算,机台成本按货币算等),形成一个可横向对比的系数。这种情况我们在设定优化策略时,可以将需要考虑的因素集合,通过一个数学模型进行去量纲化,从而实现引擎以计算后的系数为基础进行方案评分。
由于情况过于复杂,本文不列举示例。通过易排平台的规划策略设定,可以实现该需求;但众多项目实践证明,需要将不同的因素综合在一起形成系数,需要大量的数据验证,否则得到的转化模型很难考虑周全。此外,通过这种系数评分体系得到的方案,在验证方面也是巨大的挑战,也就是面对引擎排出来的方案,当你需要验证它是否符合指定的策略意图时,也相当复杂。
硬约束与软约束
上文提到的规划模型中的某些不可违反的“前提条件”,是指我们业务约束中必须符合的要求的集合,我们称之为硬约束。在规划模型中通常用subject to部分表示(称为“受限于”),例如我在一篇介绍Google - OR-Tools的文章中提到基于OR-Tools建立的简单数学模型示例中,s.t.部分,如下图红框部分(该文章尚未发表在本公众号,可到知乎等平台上搜索《OptaPlanner与Google OR-Tools的区别》)。
相对于硬约束,还有部分约束被设计成软约束,以数学规划模型来看,就是目标函数,即下图绿框部分。
求解器(即规划引擎)在求解时,基于subject to部分为前提,求目标函数z取得极值时,各个规划变量的值,即下图的x, y的值.
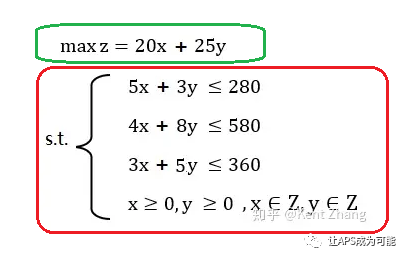
在OptaPlanner中,subject to部分使用硬约束实现,而目标函数则使用软约束来实现。事实上当业务场景相当复杂时,形成的数学模型也将会相当复杂。但OptaPlanner中的规划模型无需建立数学模型,也即无需将业务约束通过数学表达式表示出来,只需通过Java的各种类反映各业务实体,再通过约束表达式(以前使用Drools脚本,现在使用ConstraintStream来表达,也可以直接通过Java代码来表示)实现硬约束与软约束。
在OptaPlanner中,生成的所有备选方案中,若一个方案违反了硬约束(即数学模型中的subject to),则被称为不可行方案,否则称为可行方案。例如,“任务A只能使用A类设备加工”被定义为个硬约束,当一个方案中它被分配到其它A类以外的设备上加工时,即违反了硬约束,这个方案被称为不可行方案。
而一些约束可以被违反,即使违反了这类约束的方案,仍然是可行方案;但不违反比违反更佳,违反得少比违反得多更佳。这类约束我们称为软约束。上述的资源负责均衡、资源最优策略,明显属于这类软性要求,因此,在OptaPlanner/TimeFold中通过软约束实现。
例如,成本最优中,通过资源被占用天数乘以单位时间成本作为方案成本,作为成本最优这个约束的计划公式。引擎在对各个方案评分过程中,就会按此公式进行计算,去寻找成本最低的方案。评分函数可表达如下
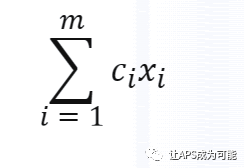
其中,ci表示第i个设备的单位时间使用成本,xi表示第i个设备每个月占用天数。
实际排产场景中,上述提出的各种优化策略单独存在,只是最理想的情况,实际排产中,除了资源成本(或任务均衡)这一个软约束,我们还需要考虑更多其它制约因素,从而形成一个复杂的多目标优化问题。需要将这些目标综合在一起,根据实际业务情况理清各自的层次与权重,才能建立高质量的规划模型。
易排平台台的策略选择
在易排平台上,我们开放了一个规划策略选择,可以基于您的选择来指令引擎遂行相应的策略。这个功能我们将在1.5.1版本推出。

<完>
我们的易排平台就是基于OptaPlanner求解器做的一个一定程序上对Job Shop Scheduling场景的泛化,可以最大程度上适配各种复杂的生产计划和车间调度情况。需进一步了解,可以关注公从号【让APS成为可能】获取更详细资料,或添加本人微信 13631823503详细探讨。