_11LeetCode代码随想录算法训练营第十一天-C++队列的应用

239.滑动窗口最大值
347.前K个高频元素

239.滑动窗口最大值

整体思路

要实现一个单调递减队列：

对于滑动窗口的滑动，移除前面的元素，加入后面的元素。当移除前面的元素时，如果当前这个元素等于队头元素，那么就出队；当加入后面的元素时，如果队尾的元素小于这个元素，那么就将队尾元素出队，直到队尾元素小于这个元素时，将这个元素入队。这样队首元素即为当前滑动窗口的最大值。

这样的队列维护了每次滑动窗口的最大值信息，而且不用存储滑动窗口所有的值，就挺好的。

代码

/*
 * @lc app=leetcode.cn id=239 lang=cpp
 *
 * [239] 滑动窗口最大值
 */

// @lc code=start
class Solution {
private:
    class myQuene
    {
    private:
        deque<int> dq;//这是一个双向队列，可以从队首队尾都可以作为入口和出口
    public:
        void push(int data)
        {
            //出队列的情况
            while(!dq.empty() && data > dq.back())
                dq.pop_back();
            dq.push_back(data);
        }
        void pop(int data)
        {
            //入队列的情况
            if(!dq.empty() && dq.front() == data)
                dq.pop_front();
        }
        int front()
        {
            return dq.front();
        }
    };
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> res;
        myQuene mq;
        //首先将前k个元素入队列
        for(int i = 0; i < k; i++)
        {
            mq.push(nums[i]);
        }
        //将第一个滑动窗口的最大值存起来；
        res.push_back(mq.front());
        for(int i = k; i < nums.size(); i++)
        {
            mq.pop(nums[i-k]);
            mq.push(nums[i]);
            res.push_back(mq.front());//将当前滑动窗口的最大值存储起来
        }
        return res;//返回结果
    }
};
// @lc code=end

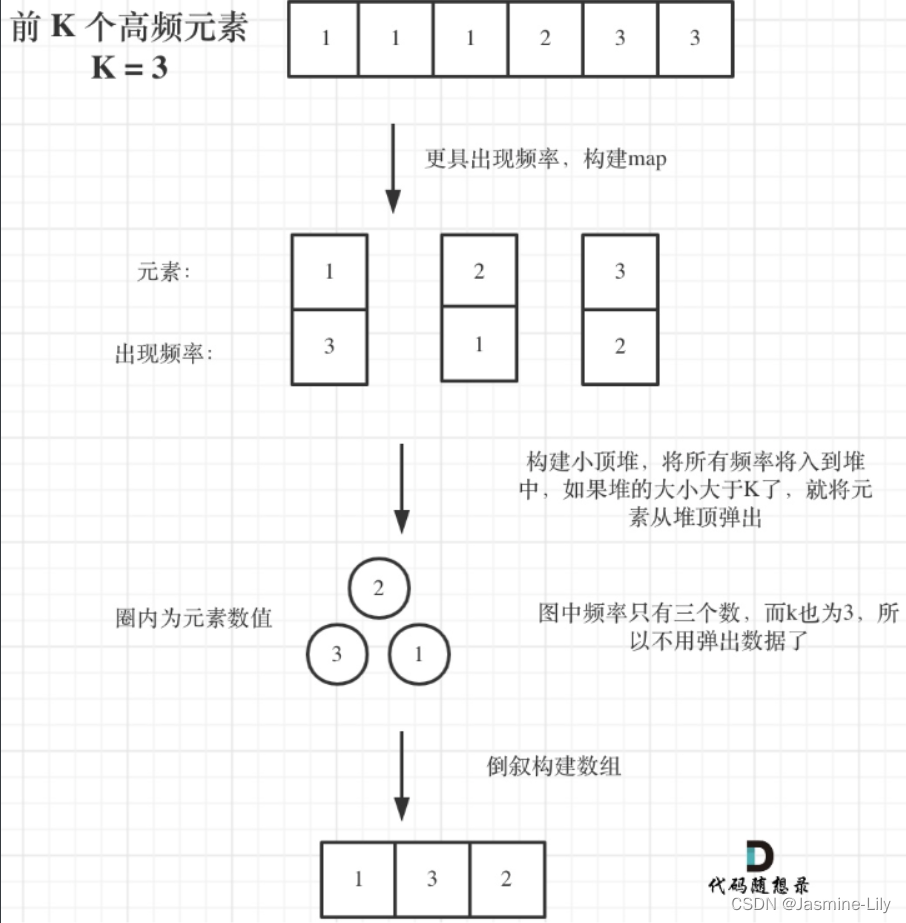
347.前K个高频元素

优先级队列

优先级队列对外接口只是从队头取元素，从队尾添加元素。

优先级队列内部元素是自动依照元素的权值排列。

排列的方式：缺省情况下priority_queue利用max-heap（大顶堆）完成对元素的排序，这个大顶堆是以vector为表现形式的complete binary tree（完全二叉树）。

堆

堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。

整体思路

为什么不用快排？

使用快排要将map转换为vector的结构，然后对整个数组进行排序，而这种场景下，我们其实只需要维护k个有序的序列就可以了，所以使用优先级队列是最优的。

使用大顶堆还是小顶堆？

使用大顶堆的话，每次弹出的是最大值，然后大顶堆里面存储的就不是频率为前k的元素；使用小顶堆的话，每次弹出的是最小值，然后小顶堆里面存储的就是频率为前k的元素。

在这里插入图片描述

代码

/*
 * @lc app=leetcode.cn id=347 lang=cpp
 *
 * [347] 前 K 个高频元素
 */

// @lc code=start
class Solution {
public:
    class myCompare{
        public:
        bool operator()(pair<int,int>& left,pair<int,int>& right)
        {
            return left.second > right.second;
        }
    };
    vector<int> topKFrequent(vector<int>& nums, int k) {
        //统计元素出现的频率
        unordered_map<int, int> map;
        for(int data : nums)
        {
            map[data]++;
        }
        //对频率进行排序
        //这里的第三个参数必须是类，不能是函数
        priority_queue<pair<int, int>, vector<pair<int, int>>, myCompare> priQueue;
        for(auto it = map.begin(); it != map.end(); it++)
        {
            priQueue.push(*it);
            if(priQueue.size() > k)
                priQueue.pop();
        }
        //取出元素
        vector<int>res;
        for(int i = 0; i < k; i++)
        {
            res.push_back(priQueue.top().first);
            priQueue.pop();
        }
        return res;
    }
};
// @lc code=end