【每日一题】1971. 寻找图中是否存在路径

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n -1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径，则返回 true，否则返回 false 。

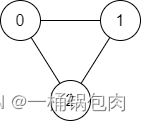
输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:

• 0 → 1 → 2
• 0 → 2

题目解析

【广度优先搜索】：从顶点出发，找到该点所能到达的其他顶点，并存入到队列中。之后每次从队列中取出队头顶点，将该点所能到达的其他顶点压入到队列中。

class Solution {
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        if(source == destination) return true;
        // 使用邻接表存储
        Map<Integer, List<Integer>> map = new HashMap<>();
        for(int[] e : edges){
            List<Integer> list = map.getOrDefault(e[0], new ArrayList<>());
            list.add(e[1]);
            map.put(e[0], list);

            list = map.getOrDefault(e[1], new ArrayList<>());
            list.add(e[0]);
            map.put(e[1], list);
        }
        // 广度优先
        Deque<Integer> queue = new LinkedList<>();
        boolean[] flag = new boolean[n];
        //顶点
        flag[source] = true;
        if(map.get(source) == null) return false;
        for(Integer i : map.get(source)){
            queue.addLast(i);
            flag[i] = true;
        }
        while(!queue.isEmpty()){
            int node = queue.removeFirst();
            if(node == destination) return true;
            if(map.get(node) == null) continue;
            for(Integer i : map.get(node)){
                if(flag[i]) continue;
                queue.addLast(i);
                flag[i] = true;
            }
        }
        return false;
    }
}

【深度优先搜索】：使用递归，每遇到一个顶点，一直向下搜索。

class Solution {
    boolean[] flag;
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        if(source == destination) return true;
        flag = new boolean[n];
        // 使用邻接表存储
        Map<Integer, List<Integer>> map = new HashMap<>();
        for(int[] e : edges){
            List<Integer> list = map.getOrDefault(e[0], new ArrayList<>());
            list.add(e[1]);
            map.put(e[0], list);

            list = map.getOrDefault(e[1], new ArrayList<>());
            list.add(e[0]);
            map.put(e[1], list);
        }
       // 递归
       return dfs(map, source, destination);

    }

    public boolean dfs(Map<Integer, List<Integer>> map, int source, int destination){
        if(source == destination) return true;
        if(map.get(source) == null) return false;
        for(Integer i : map.get(source)){
            if(flag[i]) continue;
            flag[i] = true;
            if(dfs(map, i, destination)) return true;
        }
        return false;
    }
}

【并查集】

class Solution {
    // 并查集模版！
    class UnionFind {
        private int[] parent;

        public UnionFind(int n) {
            parent = new int[n];
            for (int i = 0; i < n; i++) {
                parent[i] = i;
            }
        }

        public int find(int x) {
            if (x != parent[x]) {
                parent[x] = find(parent[x]);
            }
            return parent[x];
        }

        public void union(int x, int y) {
            parent[find(x)] = parent[find(y)];
        }
    }

    public boolean validPath(int n, int[][] edges, int source, int destination) {
         UnionFind uf = new UnionFind(n);
         // 一条边的两个点 属于一个集合
        for (int[] edge : edges) {
            uf.union(edge[0], edge[1]);
        }
        return uf.find(source) == uf.find(destination);
    }
}

【leetcode hot 100】739. 每日温度

题目描述

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

题目描述

【单调栈】：该题可以使用单调栈。从后向前遍历，栈从上到下存放温度递增的顺序。
【入栈】：将当前温度压入栈
【出栈】：如果栈顶温度小于当前温度，则将栈顶出栈。

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        // 单调栈
        // 栈中存放的是 温度递增的顺序
        Deque<Integer> stack = new LinkedList<>();
        int[] re = new int[temperatures.length];
        stack.push(temperatures.length - 1);
        for(int i = temperatures.length - 2; i >= 0; i--){
            while(!stack.isEmpty() && temperatures[stack.peek()] <= temperatures[i]){
                stack.pop();
            }
            if(stack.isEmpty()){
                re[i] = 0;
            }else{
                re[i] = stack.peek() - i;
            }
            stack.push(i);
        }
        return re;
    }
}

【代码随想录】 860. 柠檬水找零

题目描述

在柠檬水摊上，每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5美元。

注意，一开始你手头没有任何零钱。

给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

输入：bills = [5,5,5,10,20]
输出：true
解释：
前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零，所以我们输出 true。

题目解析

class Solution {
    public boolean lemonadeChange(int[] bills) {
        int[] b = new int[3];
        for(int i : bills){
            if(i == 5){
                b[0]++;
            }else if(i == 10){
                if(b[0] > 0){
                    b[0]--;
                    b[1]++;
                }else{
                    return false;
                }
            }else{
                if(b[1] > 0 && b[0] > 0){
                    b[0]--;
                    b[1]--;
                }else if(b[0] >= 3){
                    b[0] -= 3;
                }else{
                    return false;
                }
            }
        }
        return true;
    }
}