如果说组合问题可以说是思考如何使用回溯算法收割叶子节点的结果、
那么子集问题就是思考如何使用回溯算法收割每一个节点的结果
回溯算法的解题三部曲:1.确定传入的参数 2.确定终止条件 3.确定单层遍历逻辑
78. 子集
本题就是经典的子集问题了,那么使用回溯算法的解题三部曲来解决问题
1.确定传入的参数 本题只需要传入题目给定的数组以及下一层遍历起始位置即可
public void subsets(int[] nums,int startIndex)2.确定终止条件
子集问题中我们其实不需要终止条件,因为我们需要收割每一个节点的结果,但是我们也可以写上终止条件比如
if(startIndex >= nums.length){
return;
}3.确定单层遍历逻辑
由于我们需要把每一个节点的结果都放进结果集内,所以我们只需要在每一层递归里面都将上一层的结果放进结果集内即可
ans.add(new ArrayList(path));
for(int i = startIndex;i < nums.length;i++){
path.add(nums[i]);
subsets(nums,i+1);
path.removeLast();
}最后贴上我们完整代码
class Solution {
List<List<Integer>> ans = new ArrayList();
LinkedList<Integer> path = new LinkedList();
public List<List<Integer>> subsets(int[] nums) {
subsets(nums,0);
return ans;
}
public void subsets(int[] nums,int startIndex){
ans.add(new ArrayList(path));
if(startIndex >= nums.length){
return;
}
for(int i = startIndex;i < nums.length;i++){
path.add(nums[i]);
subsets(nums,i+1);
path.removeLast();
}
}
}90. 子集 II
本题就是上一题的基础上增加了一点点难度 我们应该如何完成去重操作?
这个问题其实在组合问题我们已经解决了:
先将数组进行排序好然后前一个数字与当前数字重复时,我们就跳过当前循环,执行下一次循环
原因在于前一个数字所构成的组合与当前数字构成的组合是一样的,所以我们可以跳过当前循环避免重复操作
if(i > startIndex && nums[i] == nums[i-1]){
continue;
}这里需要注意的是 我们的 i 是 i > startIndex 而不是 i > 0
如果我们将 写成 i > 0 那么就会出现这种情况

很明显如果写成 i > 0 那么就一定会漏掉很多结果,原因在于 写成 i > 0就会导致树枝去重,在 1 这个树枝上都会完成去重操作,但是如果写成 i > startIndex 我们就能保证只在树层去重而不是树枝去重
在这里我画了简单一个图来帮助大家理解什么叫做树枝和树层
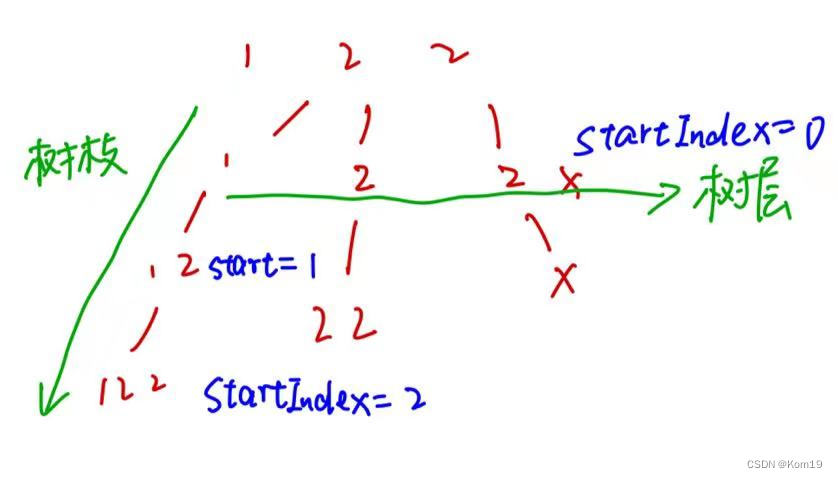
最后贴上我们的完整代码
class Solution {
List<List<Integer>> ans = new ArrayList();
LinkedList<Integer> path = new LinkedList();
public List<List<Integer>> subsetsWithDup(int[] nums) {
Arrays.sort(nums);
subsetsWithDupHelper(nums,0);
return ans;
}
public void subsetsWithDupHelper(int[] nums,int startIndex){
ans.add(new ArrayList(path));
if(startIndex >= nums.length){
return;
}
for(int i = startIndex;i < nums.length;i++){
if(i > startIndex && nums[i] == nums[i-1]){
continue;
}
path.add(nums[i]);
subsetsWithDupHelper(nums,i+1);
path.removeLast();
}
}
}491. 递增子序列
这题乍一看好像和刚才的子集II问题是一样的,同样是去重与收集子集
但是我们要注意题目的要求是递增子序列
我们在子集II问题中首先对数组进行了排序 然后再进行一系列操作,但是如果这一题也使用排序,那么不就打乱了题目原本的顺序了吗?数组内的数字永远都是递增的,所以上一题的解法在这里不适用
那么怎么才能解决这题呢?
实际上在组合问题里面我们提到过相关的解法,可以使用一个数组来标记哪一些数字使用过,从而达到不使用排序也可以完成去重效果
依旧使用我们的回溯三部曲:
1.确定参数
public void findSubsequencesHelper(int[] nums,int startIndex)2.确定终止条件
if(path.size() > 1){
result.add(new ArrayList(path));
}3.确定单层遍历的逻辑
我在这里使用的Set这个数据结构来帮助我完成树层去重的操作,大家也可以使用数组的形式进行树层去重
HashSet<Integer> set = new HashSet();
for(int i = startIndex;i < nums.length;i++){
if(!path.isEmpty() && path.get(path.size() - 1) > nums[i]
|| set.contains(nums[i])){
continue;
}
set.add(nums[i]);
path.add(nums[i]);
findSubsequencesHelper(nums,i+1);
path.removeLast();
}注意我这里在进行是否是递增子序列的判断时使用的是链表的最后一位数字与当前数字进行比较
为什么呢?我这里举一个例子
[1,2,3,4,5,6,7,8,9,10,1,1,1,1,1]
当出现这种例子时,如果使用的是
if(i > 0 && nums[i] >= nums[i-1]
|| set.contains(nums[i])){
continue;
}那么最后输出的一个结果肯定包括
[1,2,3,4,5,6,7,8,9,10,1,1,1,1]
原因就在于我们是在数组里面进行比较的,不能保证我们的子序列一定是递增的,但是如果我们使用链表的最后一位数字与当前数字进行比较那么就没有这个问题了
46. 全排列
这里实际上还是子集问题,唯一不同的是我们每层循环的开始位置都是0,同时我们需要使用一个used数组来标记哪些数字使用过
简单画一个树状图(关键分支)
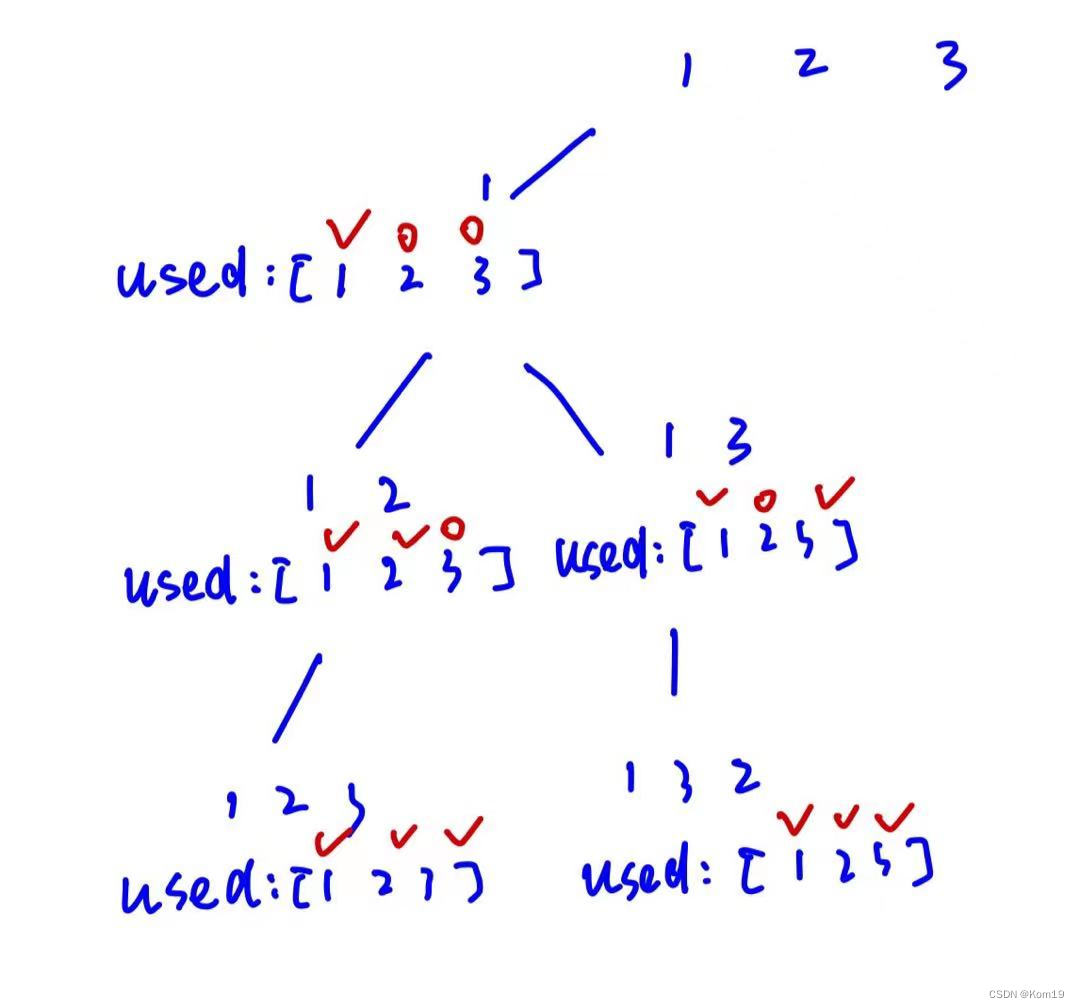
递归三部曲:
1.确定参数:由于我们每层循环的开始位置都是0,所以不需要传入下一层的起始位置了
public void permuteHelper(int[] nums)2.确定终止条件
当我们的path的长度与数组的长度相等时说明此时就完成全排列
if(path.size() == nums.length){
ans.add(new ArrayList(path));
}3.确定单层遍历条件
for(int i = 0;i < nums.length;i++){
if(used[i] == true){
continue;
}
path.add(nums[i]);
used[i] = true;
permuteHelper(nums);
used[i] = false;
path.removeLast();
}当我们的used数组是true,说明这个数字已经被使用过了,那么就跳过本次循环,进入下一次循环,当回溯到本层时,我们就需要把这个used再调整成未被使用的状态
最后贴上完整代码
class Solution {
List<List<Integer>> ans = new ArrayList();
LinkedList<Integer> path = new LinkedList();
boolean[] used;
public List<List<Integer>> permuteUnique(int[] nums) {
used = new boolean[nums.length];
Arrays.sort(nums);
permuteUniqueHelper(nums,0);
return ans;
}
public void permuteUniqueHelper(int[] nums,int startIndex){
if(path.size() == nums.length){
ans.add(new ArrayList(path));
}
for(int i = 0;i < nums.length;i++){
//used[i-1] == false表示树层去重
if(i > 0 && nums[i] == nums[i-1] && used[i-1] == true){
continue;
}
if(used[i] == true){
continue;
}
path.add(nums[i]);
used[i] = true;
permuteUniqueHelper(nums,i+1);
used[i] = false;
path.removeLast();
}
}
}47. 全排列 II
本题就是在上一题进行了一点拓展,如何进行去重操作之前的题目也讲过了,这里就不重复赘述了
但本题的关键在于如何进行去重的逻辑
if(i > 0 && nums[i] == nums[i-1] && used[i-1] == false){
continue;
}我这里使用的是 used[i - 1] == false 来进行树层去重的操作,当nums[i-1] == false时说明nums[i-1]已经完成了全排列,所以我们跳过当前循环进入到下一次循环
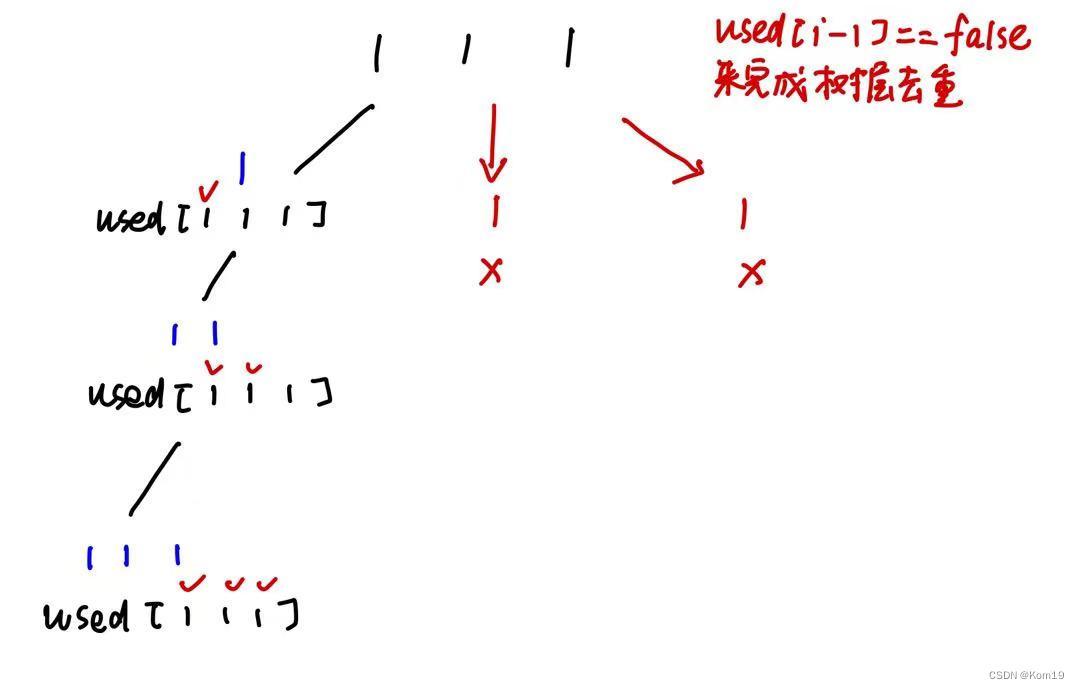
当然我们也可以使用 used[i - 1] == true 来完成去重操作,只不过如果使用 used[i - 1] == true 那么就是在树枝上完成去重了,这里同样画一幅图来说明
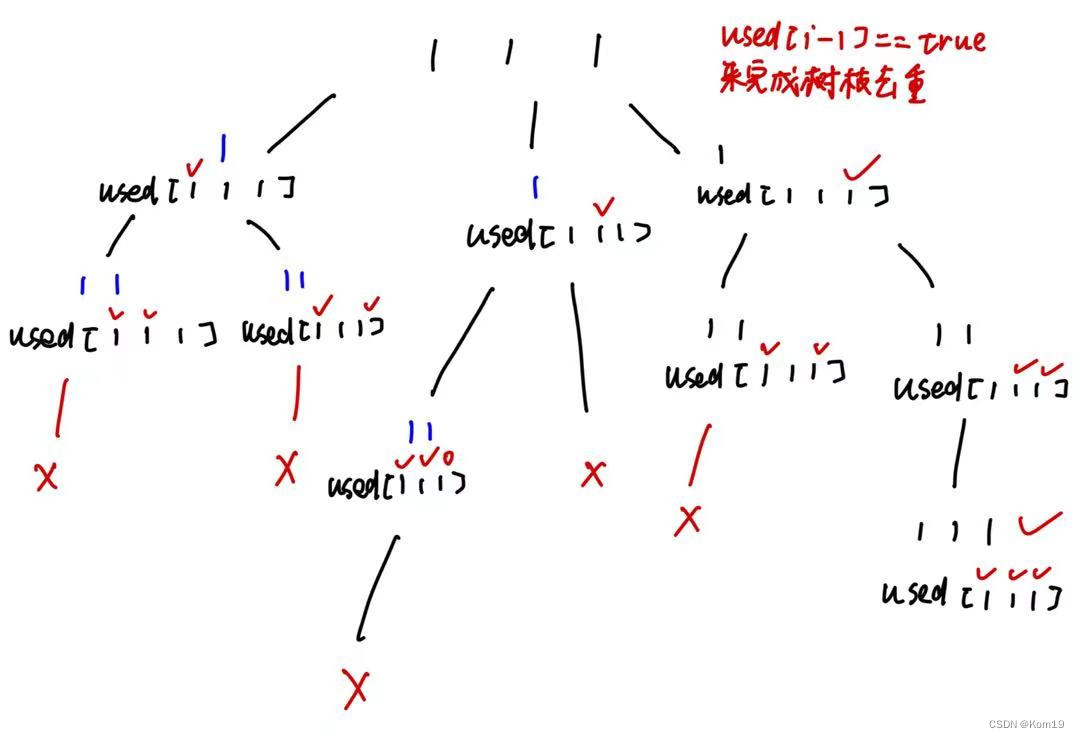
最后贴上我们的完整代码
class Solution {
List<List<Integer>> ans = new ArrayList();
LinkedList<Integer> path = new LinkedList();
boolean[] used;
public List<List<Integer>> permuteUnique(int[] nums) {
used = new boolean[nums.length];
Arrays.sort(nums);
permuteUniqueHelper(nums,0);
return ans;
}
public void permuteUniqueHelper(int[] nums,int startIndex){
if(path.size() == nums.length){
ans.add(new ArrayList(path));
}
for(int i = 0;i < nums.length;i++){
if(i > 0 && nums[i] == nums[i-1] && used[i-1] == false){
continue;
}
if(used[i] == true){
continue;
}
path.add(nums[i]);
used[i] = true;
permuteUniqueHelper(nums,i+1);
used[i] = false;
path.removeLast();
}
}
}