C. Count Binary Strings

大意：

要求满足条件的01串的个数

要求如下

给定一个上三角矩阵，对于矩阵的元素i,j,a[i][j]有一下三个取值：

=1：i-j之间只能有一种元素

=2：i-j之间只能有两种元素

=0:  i-j之间无所谓

思路：

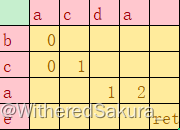
我们不妨考虑一下01串的第i位。比方说它是1，那么i-i之间是只有一个元素的，显然a[i][i]不能等于2，然后我们向前看的话，如果第i-1位也是1，那么i-1~i之间也只有一个元素；i-2位也是1的话同理，那么这些位置到1之间的要求都不能是2。如果现在前面出现了一个1，那么它以及它之前的位置到i的区间内都一定有两种元素，这时区间要求不能等于1。这其实就是我们check的要求了。

所以考虑dp[i][j]，以第i位为末尾，从后往前看第一个出现与第i位元素不同的位置为j-1的对应合法字符串的方案数。考虑一下更新，下一位要么与第位相同，那就是dp[i+1][j],如果与第i位不同，那么就是dp[i+1][i+1]。那么要check的话，每一次更新之前都把前面所有位置都看一下，有没有非法约束，所以总体复杂度就是O(n^3).然后这里dp[i][j]中取不同的位置位j-1，是是因为有可能前面全部都是相同的，那么第一次出现非法的位置就可以当作是0了。

code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=110;
const ll mod=998244353;
ll n;
ll mp[N][N];
ll dp[N][N];
bool check(ll a,ll b)//a<=b 
{
	for(int i=1;i<=b;++i)
	{
		if(mp[i][b]==0) continue;
		if(i<a&&mp[i][b]==1) return 0;
		if(i>=a&&mp[i][b]==2) return 0;
	}
	return 1;
}
void solve()
{
	cin>>n;
	for(int i=1;i<=n;++i)
	{
		for(int j=i;j<=n;++j)
		{
			cin>>mp[i][j];
		}
	}
	dp[1][1]=2;
	for(int i=1;i<=n;++i)
	{
		for(int j=1;j<=i;++j)
		{
			if(check(j,i))//i>=j
			{
				//合法
				dp[i+1][j]=(dp[i+1][j]+dp[i][j])%mod;
				dp[i+1][i+1]=(dp[i+1][i+1]+dp[i][j])%mod;
			}
			else dp[i][j]=0;
		}
	}
	ll ans=0;
	for(int i=1;i<=n;++i)
	{
		ans=(ans+dp[n][i])%mod;
	}
	cout<<ans<<endl;
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//	ll t;cin>>t;
//	while(t--)
	solve();
	return 0;
}

D. Playoff 

大意：

2^n个人打比赛，每人有一个元素ai，所有ai是2^n的一个排列.每轮随机分成两组，两组之间随机两两对决,输的淘汰。

给定01串，第i个数字为1，则第i轮所有比赛中元素值大的获胜，否则元素值小的火绳。

问所有可能获胜的人。

样例：101

第一轮大的获胜，第二轮小的获胜，第三轮大的获胜。

考虑胜者为k

一轮过后，可以发现每个人都至少比一个数字要大,k>=2。第二轮之后，每个人也都至少比一个数字要小，k<=7。最后一轮，比如胜者的对手元素值是s，s在第一轮比一个数大，所以k大于s以及s在第一轮的对手，再加上k自己在第一轮也并另一个数大，所以k至少比三个数大，k>=4,所以k能取4，5，6，7

不难发现，0和1的情况其实是同理的，而且01的出现顺序并不重要，我们只需要知道对手比多少个数大，又比多少个数小，类比一下就好了。结论就是n个数里面有a个1的话，k>=(1<<a),有b个0的话，k<=-(1<<b)+(1<<n)+1;

code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=110;
ll n;
ll mas[N][N];
void solve()
{
	cin>>n;
	char a;
	ll num=0;
	for(int i=1;i<=n;++i)
	{
		cin>>a;
		if(a=='1') num++;
	}
	if(num==n)
	{
		cout<<pow(2,n)<<endl;
		return;
	}
	ll ans=pow(2,num);
	ll d_ans=pow(2,n-num);
	for(int i=ans;i<=pow(2,n)-d_ans+1;++i) cout<<i<<' ';
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//	ll t;cin>>t;
//	while(t--)
	solve();
	return 0;
}

E. Algebra Flash 

大意：
n个格子，每一个格子有一个颜色，共m种颜色。想要经过某一个格子，要先购买对应的颜色，每次只能走1步/2步，求从1走到n所需的最小花费。颜色数m<=40;

思路：

首先由一个比较显然的结论，每两个格子之间必然有至少一个格子对应的颜色是被购买的，否则有一个跨度为2的区间，我们是走不过去的。所以如果我们将相邻格子对应的颜色之间连边的话，其实要求的就是一个花费最小的点覆盖。注意到1和n的颜色必选，所以1和n还要连一个自环。

那么如何求花费最小的点覆盖？如果直接状压枚举情况，复杂度是O（(2^m)*m*m）,炸了，但是我们发现如果m等于20的话其实复杂度是能吃下的，所以考虑分治。

将m种颜色分成两部分，大小为m/2,m-m/2，记作集合A，集合B。显然，在这种情况下，我们可以把所有边分成三种类型：端点都在A里面，端点都在B里面，还有两个端点分别在A和B里面。

对于前两种情况，其实是一样的：假设A集合里面我选了一个子集，如果剩下没选的点之间有边相连的话，那么这些边我就没有办法覆盖了，这是一个非法情况。

考虑最后一种情况：我在B中选了一些点，剩下的点的其中一个如果与A中的某个点c相连，那么c我是要选上的，不然这条边也无法覆盖了。

如此思路就比较显然了。我们枚举集合B选择情况，如果一个子集是非法的，那就跳过，否则，按照情况三，我们会在A中有一些必选的点，我们只要预处理出在选这些点的情况下，A的合法选择中的最小花费，此时的总花费就是两者之和了。更新一下就行了。

这样做的话，我们每次只用枚举一半的点数，所以复杂度成功降到了

tip：在预处理A的花费时，我们对一个子集的花费定义为A必选这个子集的情况下的所有合法选择中的最小花费。所以如果有一个选择是非法的，我们不应该跳过它，因为它加入一些点之后就是合法的了，这也就它会被它的父集合更新花费，所以我们应该倒序枚举A

code

#include<bits/stdc++.h>
using namespace std;
#define ll int
#define endl '\n'
const ll N=3e5+10;
const ll inf=0x3f3f3f3f;
ll n,m;
ll mas[N];
ll mp[50][50];
ll c[50];//花费 
ll dp[(1<<21)];
ll z1,z2;
bool check(int s,ll z,ll det)//检查是否存在两顶点均未被覆盖的边  det:偏移量 
{
	for(int i=0;i<z;++i)
	{
		if((s>>i)&1) continue;
		for(int j=i;j<z;++j)//考虑到自环，j从i开始 
		{
			if((s>>j)&1) continue;
			if(mp[i+det][j+det]) return 0;
		}
	}
	return 1;
}
void solve()
{
	cin>>n>>m;
	for(int i=1;i<=n;++i)
	{
		cin>>mas[i];
		mas[i]--;//从0开始最好，因为后面状压写起来就会比较舒服 
	}
	for(int i=0;i<m;++i)
	{
		cin>>c[i];
	}
	for(int i=1;i<=n;++i)
	{
		if(i>1) mp[mas[i]][mas[i-1]]=1;
		if(i<n) mp[mas[i]][mas[i+1]]=1;
	}
	mp[mas[1]][mas[1]]=mp[mas[n]][mas[n]]=1;//起终点必须连接，所以连一个自环
	z1=m/2;z2=m-z1;
	for(int s=(1<<z1)-1;s>=0;--s)
	{
		if(check(s,z1,0))
		{
			for(int i=0;i<z1;++i)
			{
				if((s>>i)&1) dp[s]+=c[i];
			}
		}
		else//该集合非法，由它的父集更新 
		{
			dp[s]=inf;
			for(int i=0;i<z1;++i)
			{
				if(((s>>i)&1)==0) dp[s]=min(dp[s],dp[s|(1<<i)]);
			}
		}
	}
	ll ans=inf;
	for(int s=0;s<(1<<z2);++s)
	{
		if(check(s,z2,z1)==0) continue;
		ll now=0;//该集合的花费;
		ll t=0;//上一个集合的需要的点
		for(int i=0;i<z2;++i)
		{
			if((s>>i)&1) now+=c[i+z1];
			else
			{
				for(int j=0;j<z1;++j)//从另一个集合里面去找由连边的点 
				{
					if(mp[i+z1][j]) t|=(1<<j); 
				}
			}
		} 
		ans=min(ans,now+dp[t]);
	}
	cout<<ans<<endl;
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	solve();
	return 0;
}