[NOIP2005 普及组] 采药（C++，动态规划）

题目描述

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式

第一行有 $2$ 个整数 $T$（$1\le T\le 1000$）和 $M$（$1\le M\le 100$），用一个空格隔开，$T$ 代表总共能够用来采药的时间，$M$ 代表山洞里的草药的数目。

接下来的 $M$ 行每行包括两个在 $1$ 到 $100$ 之间（包括 $1$ 和 $100$）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式

输出在规定的时间内可以采到的草药的最大总价值。

样例 #1

样例输入 #1

70 3
71 100
69 1
1 2

样例输出 #1

3

提示

【数据范围】

• 对于 $30\%$ 的数据，$M\le 10$；
• 对于全部的数据，$M\le 100$。

【题目来源】

NOIP 2005 普及组第三题

解题思路：

首先根据下面一组数据就可以排除贪心算法（尽量选取$\frac{value}{time}$高的）

4 3
2 6
2 3
3 4

所以我们采用递归的方式寻找最大值，递归的思路就是：

//dfs(t, m)会return前m株herb的max_value
int dfs(int t, int m) {//t为当前剩余时间，m代表当前是几号草药
    //返回不选或者选中的最大值
	return max(dfs(t, m - 1)/*不选*/, dfs(t - herb_arr[m].time, m - 1) + herb_arr[m].value/*选*/);
}

再加上边界判断、条件判断

int dfs(int t, int m) {
	if (m == -1 || t == 0)
		return 0;
	else if (herb_arr[m].time > t)
		return dfs(t, m - 1);
	else 
		return max(dfs(t, m - 1), dfs(t - herb_arr[m].time, m - 1) + herb_arr[m].value);
}

然后计算一下时间复杂度会发现是o($2^n$)，显然不可接受

所以进行记忆化搜索，时间复杂度是o(T*M)

int max_value[1001][101] = { 0 };
memset(max_value, -1, sizeof(int) * 1001 * 101);

int dfs(int t, int m) {
	if (m == -1 || t == 0) 
		return 0;
	else if (max_value[t][m] != -1) 
		return max_value[t][m];//记忆
	else if (herb_arr[m].time > t) 
		return max_value[t][m] = dfs(t, m - 1);
	else 
		return max_value[t][m] = max(dfs(t, m - 1), dfs(t - herb_arr[m].time, m - 1) + herb_arr[m].value);
}

实现的完整代码如下

#include <iostream>
#include <memory.h>
using namespace std;

struct herb {
	int time;
	int value;
};

struct herb herb_arr[100];
int max_value[1001][101] = { 0 };

int dfs(int t, int m) {
	if (m == -1 || t == 0) return 0;
	else if (max_value[t][m] != -1) return max_value[t][m];
	else if (herb_arr[m].time > t) return max_value[t][m] = dfs(t, m - 1);
	else return max_value[t][m] = max(dfs(t, m - 1), dfs(t - herb_arr[m].time, m - 1) + herb_arr[m].value);
}

int main() {
	int T, M;
	cin >> T >> M;
	for (int i = 0; i < M; i++) cin >> herb_arr[i].time >> herb_arr[i].value;
	memset(max_value, -1, sizeof(int) * 1001 * 101);

	cout << dfs(T, M - 1);
	return 0;
}

最长上升子序列（C++，Dilworth，贪心）

题目描述

这是一个简单的动规板子题。

给出一个由 $n(n\le 5000)$ 个不超过 $10^6$ 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。

最长上升子序列是指，从原序列中按顺序取出一些数字排在一起，这些数字是逐渐增大的。

输入格式

第一行，一个整数 $n$，表示序列长度。

第二行有 $n$ 个整数，表示这个序列。

输出格式

一个整数表示答案。

样例 #1

样例输入 #1

6
1 2 4 1 3 4

样例输出 #1

4

提示

分别取出 $1$、$2$、$3$、$4$ 即可。

解题思路：

本题其实考察的是动态规划，我也试着去动态规划了，但emmm还是定理好用

关于Dilworth定理，举几个例子就明白了

最长上升子序列长度(<) == 最少不上升子序列数目($\ge$)

最长不下降子序列长度($\le$) == 最少下降子序列数目(>)

最长下降子序列长度(>) == 最少不下降子序列数目($\le$)

最长不上升子序列长度($\ge$) == 最少上升子序列数目(<)

还可以推广，不只是大小关系，只要是”相反“的两个关系就可以，但“相反”的两个关系需要满足三个条件

（1）自反性：$a\le a$

（2）反对称性：$a\le b,b\le a,a=b$

（3）传递性：$a\le b,b\le c,a\le c$

正面求解上面四个例子左侧的问题不太容易，但是右边都可以直接贪心解决

以本题为例，贪心策略如下：

创建一个数组，然后读入一个元素（不是读到数组中）

如果数组中没有比这个元素大的元素，那么将这个元素添加到数组尾

如果有，那么寻找比这个元素大的最小元素，然后把这个元素覆盖

这个过程不需要排序就可以实现，可以思考一下为什么

最后数组中元素的数目即为所求解

AC代码如下

#include <iostream>
#include <vector>
using namespace std;

vector<int> not_upper_arr;

int main() {
	int n, num;
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> num;
		if (not_upper_arr.empty() || not_upper_arr.back() < num) not_upper_arr.push_back(num);
		else {
			size_t j = not_upper_arr.size();
			while (--j < not_upper_arr.size() && not_upper_arr[j] >= num);
			not_upper_arr[++j] = num;
		}
	}

	cout << not_upper_arr.size();
	return 0;
}

最大子段和（C++，DP）

题目描述

给出一个长度为 $n$ 的序列 $a$，选出其中连续且非空的一段使得这段和最大。

输入格式

第一行是一个整数，表示序列的长度 $n$。

第二行有 $n$ 个整数，第 $i$ 个整数表示序列的第 $i$ 个数字 $a_i$。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

7
2 -4 3 -1 2 -4 3

样例输出 #1

4

提示

样例 1 解释

选取 $[3,5]$ 子段 { 3 , − 1 , 2 } \{3, -1, 2\} {3,−1,2}，其和为 $4$。

数据规模与约定

• 对于 $40\%$ 的数据，保证 $n\le 2\times 10^3$。
• 对于 $100\%$ 的数据，保证 $1\le n\le 2\times 10^5$，$-10^4\le a_i\le 10^4$。

解题思路：

通过样例输入进行说明

首先读入2，把2作为前缀

然后读入-4，2+(-4)=-2>-4，所以如果-4是最大子段的一部分，2一定也是最大子段的一部分

再读入3，3+(-2)=1<3，所以如果3是最大子段的一部分，2和-4一定不是最大子段的一部分

再读入-1，3+(-1)=2<3，所以如果-1是最大子段的一部分，3一定也是最大子段的一部分

再读入2，2+2=4>2，所以如果2是最大子段的一部分，3和-1一定也是最大子段的一部分

再读入-4，4+(-4)=0>-4，所以如果-4是最大子段的一部分，3、-1、2一定也是最大子段的一部分

最后读入3，0+3=3==3，所以如果3是最大子段的一部分，3、-1、2、-4一定不是最大子段的一部分

本质就是尝试给每一个数连接一个前缀，使这个数变得比自己大，如果比自己小，那么就不连接这个前缀

每次比较连接前缀后和不连接前缀二者的大小时，我们都保证了得到的是最大的前缀，同时有可能我们得到的最大前缀就是所谓的最大子段

所以本题采用的策略并不能保证最后得到的是最大子段，但我们一定曾经得到过最大子段

再加上一个变量max_num，比较每次连接的结果并存入其中

所以在读入3之后虽然我们丢弃了2和-4，但我们已经把2，2、-4这两个子段中最大者存入了max_num

最后只需要输出max_num即可

AC代码如下

#include <iostream>
using namespace std;

int num_arr[2] = { 0 };
int max_num = 0;

int main() {
	int n, temp;
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> temp;
		if (i < 1) {
			max_num = temp;
			num_arr[0] = temp;
			continue;
		}
		num_arr[i % 2] = max(temp, temp + num_arr[(i + 1) % 2]);
		max_num = num_arr[i % 2] > max_num ? num_arr[i % 2] : max_num;
	}

	cout << max_num;
	return 0;
}

LCS

题目描述：

给定一个字符串 $s$ 和一个字符串 $t$ ，输出 $s$ 和 $t$ 的最长公共子序列。

输入格式：

两行，第一行输入 $s$ ，第二行输入 $t$ 。

输出格式：

输出 $s$ 和 $t$ 的最长公共子序列。如果有多种答案，输出任何一个都可以。

样例 #1

样例输入 #1

axyb
abyxb

样例输出 #1

axb

样例 #2

样例输入 #2

aa
xayaz

样例输出 #2

aa

样例 #3

样例输入 #3

a
z

样例输出 #3

样例 #4

样例输入 #4

abracadabra
avadakedavra

样例输出 #4

aaadara

说明/提示：

数据保证 $s$ 和 $t$ 仅含英文小写字母，并且 $s$ 和 $t$ 的长度小于等于3000。

解题思路：

设有两个字符串$s=<s_1,s_2,\dots ,s_n>$，$t=<t_1,t_2,\dots ,t_m>$，s和t的LCS为$z=<z_1,z_2,\dots ,z_k>$

如果$s_n=t_m$，那么$s_{n-1}$和$t_{m-1}$的LCS是$z_{k-1}$

**如果$s_n\ne t_m$，那么$s_{n-1}$和$t$（或者$s$和$t_{n-1}$）的LCS是$z\ast \ast$

根据上面的说明，可以得出以下递推公式

l e n [ i ] [ j ] = { 0 , i   =   0 或 j   =   0 l e n [ i − 1 ] [ j − 1 ] + 1 , s i = t j m a x { l e n [ i − 1 ] [ j ] ,   l e n [ i ] [ j − 1 ] } , s i ≠ t j len[i][j]=\begin{cases}0,&i\ =\ 0或j\ =\ 0\\[2ex]len[i-1][j-1]+1, &s_i=t_j\\[2ex]max\{len[i-1][j],\ len[i][j-1]\},&s_i\ne t_j\end{cases} len[i][j]=⎩ ⎨ ⎧​0,len[i−1][j−1]+1,max{len[i−1][j], len[i][j−1]},​i = 0或j = 0si​=tj​si​=tj​​

实现代码如下

#include <iostream>
using namespace std;
const int max_n = 3000;

string s, t;

string dfs(int i, int j) {
	if (i == -1 || j == -1) return "";
	else if (s[i] == t[j]) return dfs(i - 1, j - 1) + s[i];
	else {
		string temp_1 = dfs(i - 1, j), temp_2 = dfs(i, j - 1);
		return temp_1.size() > temp_2.size() ? temp_1 : temp_2;
	}
}

int main() {
	cin >> s >> t;
	cout << dfs(int(s.size()) - 1, int(t.size()) - 1);
	return 0;
}

但这段代码会TLE，需要进行动态优化

关于动态优化的策略，这里举例进行说明

s="adca",t="eacb"

lcs="ac"

第一次ret

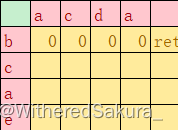
第二次ret

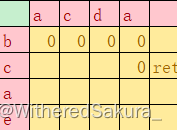
第三次ret

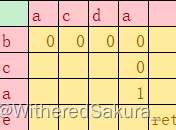
第四次ret

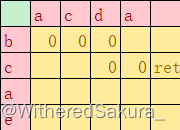
第五次ret

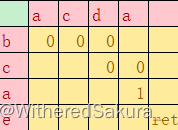
到这里应该就能看出来可以优化的地方了：第2行第4列被搜索了两次

但是并不是简单记住这次搜索后的结果就可以了

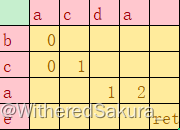
对于第二行第四列，我们可以得到不同的搜索结果

那么会想到再多记录一些信息（如记录i和j）进行判断，但那样先不说优化效果不好，占用的空间也是不可接受的

所以进一步思考，（1）我们可以优化的情形是$s_i\ne t_j$时（2）$s_i\ne s_j$时，来到同一格子的方式只有两种

那么我们只要选择左与上中较大者即可

但问题又来了，左与上可能是空格子，原因是当$s_i=t_j$时会发生跳转

再思考一下会发现，（3）如果$s_n=t_m$，那么$s_{n-1}$和$t_{m-1}$的LCS是$z_{k-1}$，与此同时$s_{n-1}和t_m$（或$s_n和t_{m-1}$）的LCS也同样是$z_{k-1}$

那么就可以在$s_i=t_j$时将其右和下的格子都填上跳转后的结果

至此，动态优化策略说明完成，优化后的策略如下：

用for循环遍历每一个格子

如果$s_i=t_j$，将上方格子的值+1填入，同时填入右（这里不填入下，也可以思考一下为什么）

如果$s_i\ne t_j$，选择左和上的格子中较大者填入

（然后emm觉得优化后和优化前好像都不是一道题了）

之所以$s_i=t_j$时直接取上方格子的值，是因为此时临近格子的值一定是相同的，可以自行用递推证明一下为什么

AC代码如下

#include <iostream>
#include <string>
#include <memory.h>
using namespace std;
const int max_n = 3000;

string s, t;
short num_arr[max_n + 1][max_n + 1] = { 0 };
string str_arr[max_n + 1][max_n + 1];

int main() {
	cin >> s >> t;
	memset(num_arr, -1, sizeof(short) * max_n * max_n);
	for (int i = s.size(); i >= 0; i--) {
		for (int j = t.size(); j >= 0; j--) {
			if (i == s.size() || j == t.size()) {//初始化
				num_arr[i][j] = 0;
				str_arr[i][j] = "";
				continue;
			}

			if (num_arr[i][j] != -1) continue;//访问过
			
			if (s[i] == t[j]) {//s_i == t_j
				str_arr[i][j] = s[i] + str_arr[i + 1][j];
				num_arr[i][j] = num_arr[i + 1][j] + 1;
				if (j - 1 > -1) {//尝试填充右
					str_arr[i][j - 1] = str_arr[i][j];
					num_arr[i][j - 1] = num_arr[i][j];
				}
			}
			else {//s_i != t_j
				if (num_arr[i][j + 1] > num_arr[i + 1][j]) {//比较并填充左、上较大者
					str_arr[i][j] = str_arr[i][j + 1];
					num_arr[i][j] = num_arr[i][j + 1];
				}
				else {
					str_arr[i][j] = str_arr[i + 1][j];
					num_arr[i][j] = num_arr[i + 1][j];
				}
			}
		}
	}
	cout << str_arr[0][0];
	return 0;
}