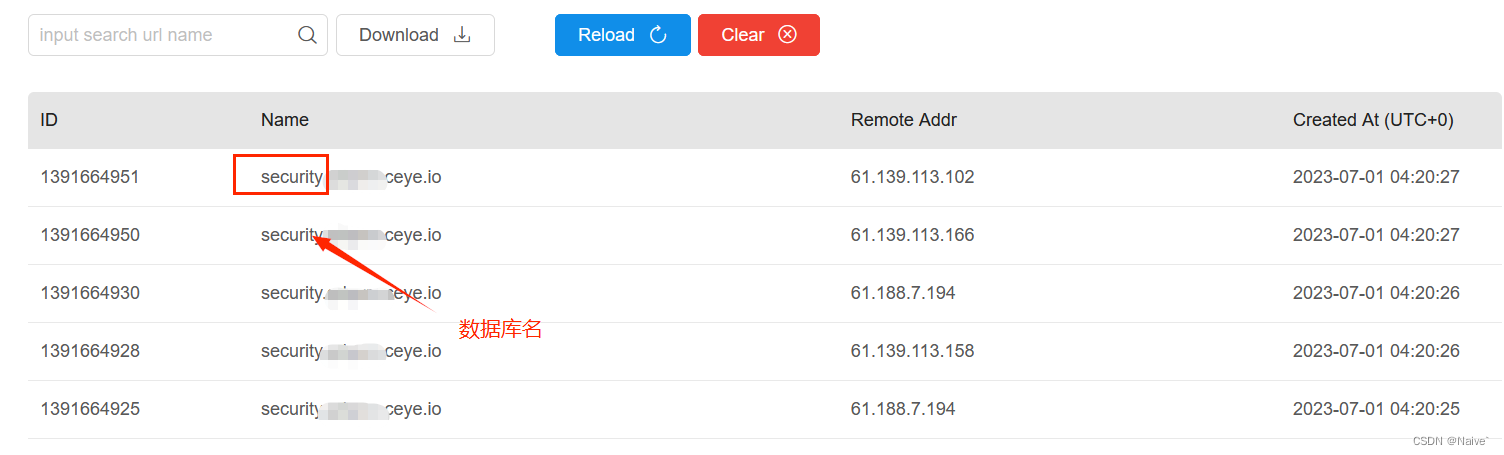
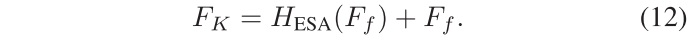二维前缀和

news2024/10/5 16:27:20

导言

当我们需要求到某个矩阵的子矩阵的和时,就可以使用二维前缀和

这是一个矩阵, $S_{ij}$ 就是左上角区域的所有数之和 $a_{11}$ + $a_{12 }$ ...... + $a_{i1 }$ + $a_{i2 }$ + $a_{i3 }$ + $a_{ij }$

如果要求中间的子矩阵的和,(x,y)为左上角 $a_{xy}$ + $a_{x y+1 }$ ...... + $a_{i1 }$ + $a_{i2 }$ + $a_{i3 }$ + ...... + $a_{ij }$ ,(i,j)为右下角,那么只需要算 $S_{ij}$ - $S_{i y-1}$ - $S_{x-1 j}$ + $S_{x-1 y-1}$ ------这一步要看清楚下标,的结果就可以了,如图

蓝色区间的面积减去红色区域的面积减去绿色区域的面积,这时发现黑色区域的面积被减了两遍,所以还要加一次黑色区域的面积, 这样就求出了中间子矩阵的面积

初始化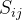 $S_{ij}$

遍历整个矩阵

公式 : $S_{ij}$ = $S_{x-1 y}$ + $S_{x y-1}$ - $S_{x-1 y-1}$ + $a_{ij }$ 每一个 $S_{ij}$ 都满足这个公式

练手

来道题,练练手!

题目
输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数×1，y1，×2，y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数n，m，q。
接下来n行，每行包含m个整数，表示整数矩阵。
接下来q行，每行包含四个整数×1，y1，×2，y2，表示一组询问。

输出格式
共q行，每行输出一个询问的结果。

数据范围
1 ≤ n ， m ≤ 1000
1 ≤ q ≤ 200000
1 ≤ x 1 ≤ x 2 ≤ n
1 ≤ y 1 ≤ y 2 ≤ m
-1000 ≤ 矩阵内元素的值 ≤ 1000

输入样例
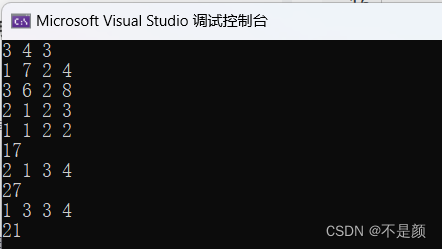
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例
17
27
21

代码实现

#include <iostream>

using namespace std;

const int N = 1010;
int a[N][N];
int S[N][N];

int n, m;
int q;
int main(void)
{
	scanf("%d%d%d", &n, &m, &q);

	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			scanf("%d", &a[i][j]); 
		}
	}

	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j]; //初始化S数组
		}
	}


	int x1, y1, x2, y2;
	while (q--)
	{
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
		printf("%d\n", S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1]);
	}


	return 0;
}