1. 集合
1.1 集合的由来和确定性
确定对象构成的整体称为集合(组成集合的元素必须是确定的 ),每个集合内的对象个体成为元素(Element)。
确定性: 给定一个集合,任何一个对象是不是这个集合内的元素,就已经确定了。
比如,我国的四大发明,造纸术,印刷术,火药,指南针。就是一个明确的构成,这个集合就是四大发明。
四大发明 = {造纸术,印刷术,火药,指南针}
每个集合内的元素,使用逗号隔开。
元素和集合之间,存在 属于/不属于 两种关系,拿上面的四大发明集合来讲,比如:
造纸术属于四大发明集合;手机不属于四大发明集合;
火药属于四大发明集合;机关枪不属于四大发明集合;
为了方便书写,采用方便的符号形式来进行代替。
属于: ∈ 不属于: ∉
在用上述的例子,替换为符号就是
造纸术 ∈ 四大发明集合;手机 ∉ 四大发明集合;
火药 ∈ 四大发明集合;机关枪 ∉ 四大发明集合;
如果给定一个集合, {大学计算机系所有的高个子学生},那么这就是一个没有办法确定的内容,不能形成一个集合。你没办法明确知道高个子到底是多高。 如果是 {大学计算机系所有身高 > 170的高个子学生},那么这就给我们划分了一个很明确的界限,大于 170 cm 的同学,都可以被划分为高个子学生列表。那么就能形成一个集合。
测试题
1. 大于 3 小于 11 的偶数。 (是)
2. 我国的小河流。 (不是)
3. 所有的正方形。 (是)
4. 本班跑步很快的同学。 (不是)
5. 与1接近的实数的全体。 (不是)
6. 1——10以内的全体质数。 (是)
总结
1. 集合是一个由确定对象构成的整体。
2. 集合内的对象称为元素(Element)。
3. 属于 ∈ / 不属于 ∉
4. 集合的确定性,给定一个集合,任何一个对象是不是这个集合内的元素,就已经确定了。
5. 可见,对于给定一个集合和给定一个对象,这个对象是否为这个集合的元素,只有 “是” 与 “不是”,这两种情况,这就是集合中元素
所具有的确定性。
1.2 集合中元素的特性

-
确定性
借鉴上面。 -
互异性
在集合中,集合内的元素必须是互异的,也就是说,对于一个给定的集合,他的任何两个元素都是不同的。
因为集合中的元素是没有重复现象的,所以任何两个相同的元素在同一集合内,只能算作这个集合中的一个元素。
- 无序性
集合与其中元素的排列次序无关,也就是说集合中的元素是不排序的。
例如: {1, 2} 也可以写成 {2, 1},他们两个是一样的。
1.3 常见数集
1.3.1 学习目标
- 理解常见数集的定义。
- 熟记常见数集的符号。
- 会判断数字与不同数集之间的关系。
1.3.2 自然数(Natural Number) 用以计量事物的件数 : N
自然数英语为 Natural Number, 所以用 大写 N 来表示自然数集。
N = {1, 2, 3, 4, 5, 6, 7...}
在1993年对于自然数集做了重新定义,定义为:
- 不小于 0 的所有整数叫 自然数集 / 非负整数 的集,也就是说,0 也是自然数集内的元素
扩展,在中国大陆2000年后的数学教材,自然数集内都包括 0。
在N后做一些特殊标记也有不同的意义,比如:
- N* : 除0意外的自然数集
- N+ : (+可以在N上面,也可以在N下面)正自然数集。
- 以此类推…
1.3.2 整数集(Whole Number): Z
整数并没有用 W 来表示整数集,有一种说法是:德国女数学家,诺特 (1882-1935)德意志数学家,抽象代数的奠基人,她提出的整数环对于整数有重大的意义 所以整数取得是德语 Zahlen(支付,数字)的首字母,Z。
Z = {0, 1, -1, 2, -2....}
1.3.3 分数 (两个整数之比 — 商)
分数,指的是两个整数之比,古希腊数学家毕达哥拉斯提出了万物皆数的概念,还发现了著名的黄金比例。他们认为,整数和分数,就可以解释整个世界了。
1.3.4 有理数:两个整数之比 — 商(Quotient) : Q
所以,有理数采用商的首字母,Q来表示有理数集。准确来说。有理数包括整数和分数
- Q = {整数和非零整数的比}
整数也可以表示成 9/1 (一分之九),8/1,5/1。 分数也可以表示为, 1/2, 3/8, 1/3
1.3.5 无理数:根号二是有理数吗?
并不是,常见的无理数有,开不尽的根号。 根号3,根号5,根号7,根号9.1 …, 无限不循环小数 Π = 3.1415926535…,自然数e等。不过到目前为止,无理数还没有统一的字幕表示。所有的有理数 + 无理数就是实数。
1.3.6 实数(Real Number):R
实数集是所有的有理数 + 无理数,实数集是目前所学的最大的数集。我们所有学习过的数字都在这个集合里面。
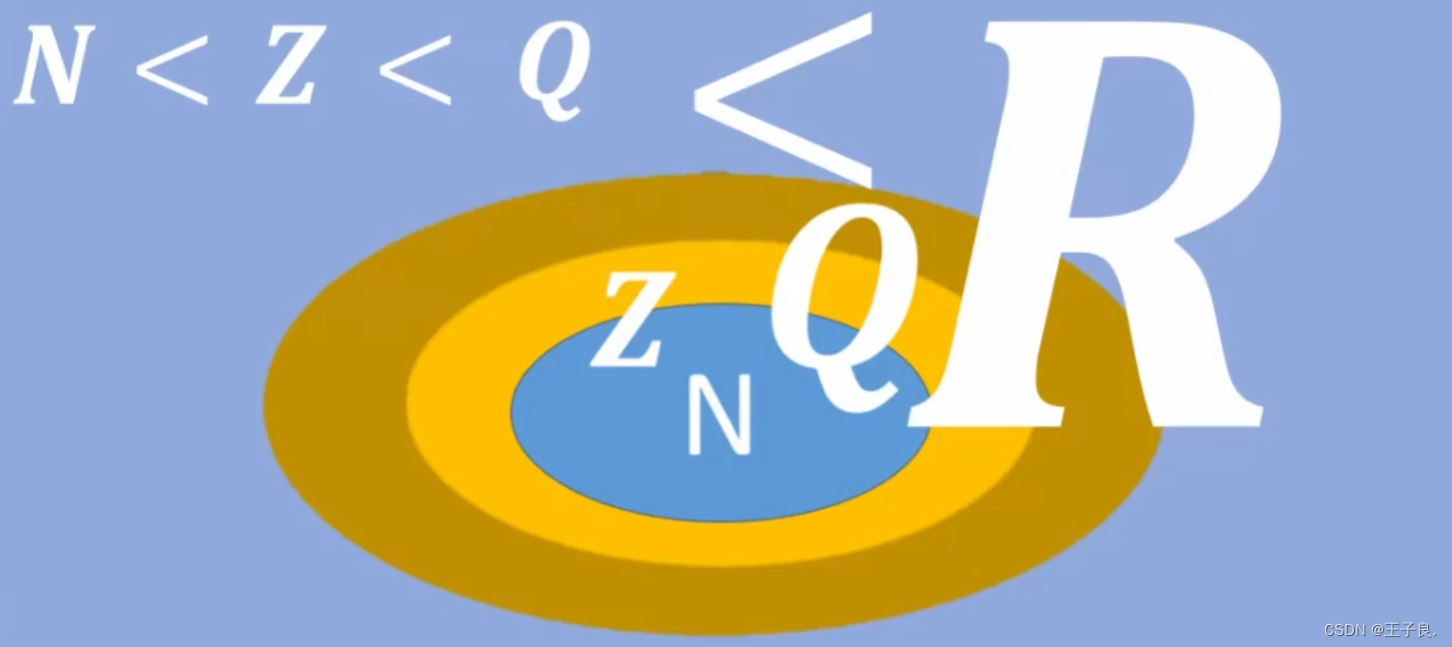
1.3.7 练习题
用符号 “∈” 或者 “∉”填空。
1. 5__N, -5__N, 0__N
2. 3__Z, -3__Z, 3.1__Z
3. 3.14__Q, Π__Q, 根号2__Q
4. Π__R, 3.1__R, 根号三__R
答案
N是自然数集,大于切等于0的整数都是数集内的内容
1. ∈,∉,∈
Z是整数集,大于小于等于0的所有整数都属于集合内的内容。
2. ∈,∈,∉
Q是有理数集,也就是两数之比和所有的整数(小数,分数,正整数,负整数,0)
3. ∈,∉,∉
R是实数集,包括了N,Z,Q,无理数集,是学习过的最大的数集
4. ∈,∈,∈
特殊符号集
1. 0__N+, 0__Z+, 0__R*
2. -3__Z+, -3__Z-, -3__Z*
答案
在数集后面跟 + 表示数集内的所有正数对象, - 表示所有的复数对象,R表示0除外的所有对象
3. ∉,∉,∉
4. ∉,∈,∈
1.3.8 总结
学习了各个数集。总结内容如下
- N(自然数集) < Z(整数集) < Q(有理数集) < R(实数集),实际上是不能这样表示的,需要稍微改造一下。
- N(自然数集) ∈ Z(整数集) ∈ Q(有理数集) ∈ R(实数集)