0 专栏介绍

🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)；局部规划(DWA、APF等)；曲线优化(贝塞尔曲线、B样条曲线等)。

🚀详情：图解自动驾驶中的运动规划(Motion Planning)，附几十种规划算法

1 栅格地图

1.1 应用场景

在这里插入图片描述

栅格地图(grid map)是在机器人和自动化领域中广泛使用的一种地图表示方法。它将环境划分为规则的网格单元，并在每个单元中存储关于该区域的信息。每个单元可以表示空闲、障碍物、未知区域或其他地图属性。

栅格地图最主要的应用是服务于机器人导航中的路径规划和避障。机器人可以利用栅格地图中的障碍物信息来规划安全的路径，并避开可能的碰撞或危险区域。同时，栅格地图也是SLAM算法中常用的地图表示方式之一。通过与传感器数据融合，机器人能够同时进行自身位置估计和地图构建。

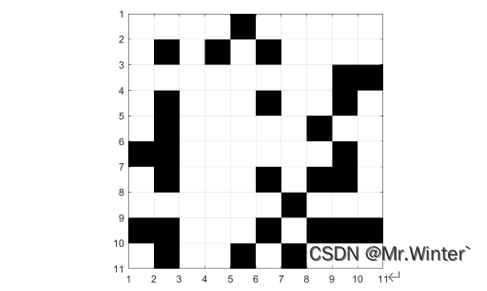
在这里插入图片描述

总之，栅格地图是一种简单且直观的地图表示方法，它可以提供对环境的可视化和语义信息，并为机器人的感知、规划和决策提供基础。然而，栅格地图也存在分辨率、存储消耗和精度等方面的限制，在实际应用中需要权衡和优化。

1.2 基本概念

栅格地图的基本概念总结如下

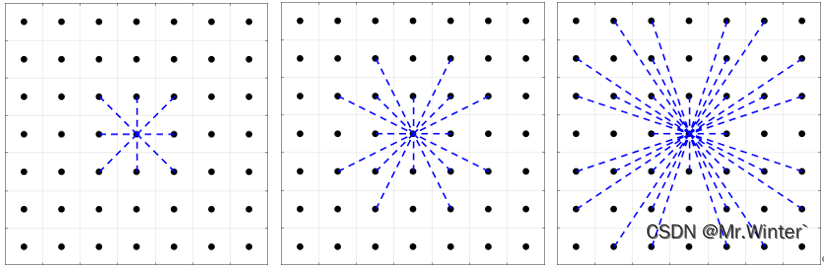
邻域模式
栅格地图中常用的邻域模式有8邻域法、24邻域法和48邻域法，如下所示
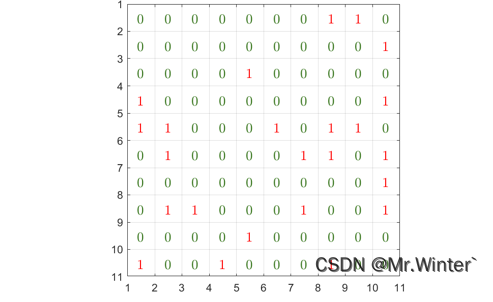
栅格示数
栅格地图中每个栅格都被赋予栅格示数，其指明了该栅格在全局环境中表达的语义。例如0表示无障碍的自由栅格，1表示障碍物
栅格坐标
栅格地图可视为离散直角坐标系，其中可用有序二元组 $(i, j)$ 定位栅格
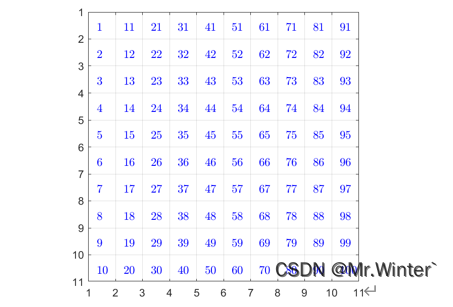
栅格序号
栅格按照行列顺序依次进行的编号称为栅格序号，由于栅格序号是一维线性的，因此可以加速信息处理与运算
栅格粒度
栅格对应物理世界的比例系数称为栅格粒度，栅格粒度越小，环境分辨率越大，对环境的刻画越具体、丰富。但相应地，存储地图所占的内存、处理地图耗费的时间越多

2 占据栅格地图

在工程上，通常使用占据法构建占据栅格地图(Occupancy Grid Map)。考虑到构建栅格地图使用的激光雷达存在噪声，即在相同条件下对障碍物的相对距离探测可能有误差，因此引入概率定义栅格状态：对于地图中的栅格 $s$ ， $P\left( s=1 \right)$ 表示栅格被占据的概率； $P\left( s=0 \right) =1-P\left( s=1 \right)$ 表示栅格自由的概率。实际应用时，使用一种更紧凑的表达

$\mathrm{odd}\left( s \right) =\frac{P\left( s=1 \right)}{P\left( s=0 \right)}$

2.1 更新模型

构建地图的问题可形式化为：已知机器人激光传感器的观测序列，更新地图中栅格的后验概率 ，根据贝叶斯公式和马尔科夫链可得

$\begin{aligned}P\left( s|z_{1:t} \right) &=\frac{P\left( z_t|s,z_{1:t-1} \right) P\left( s|z_{1:t-1} \right)}{P\left( z_t|z_{1:t-1} \right)}\\\,\, & =\frac{{ \overset{\mathrm{Markov}}{\overbrace{P\left( z_t|s \right) }}}P\left( s|z_{1:t-1} \right)}{P\left( z_t|z_{1:t-1} \right)}\\&=\frac{{ \overset{\mathrm{Bayes}}{\overbrace{P\left( s|z_t \right) P\left( z_t \right) }}}P\left( s|z_{1:t-1} \right)}{{ P\left( s \right) }P\left( z_t|z_{1:t-1} \right)}\end{aligned}$

计算后验概率优势比

$\frac{P\left( s=1|z_{1:t} \right)}{P\left( s=0|z_{1:t} \right)}=\frac{P\left( s=1|z_t \right)}{P\left( s=0|z_t \right)}\cdot \frac{P\left( s=1|z_{1:t-1} \right)}{P\left( s=0|z_{1:t-1} \right)}\cdot \frac{P\left( s=0 \right)}{P\left( s=1 \right)}$

一般令先验概率 $P\left( s=0 \right) =P\left( s=1 \right) =0.5$ ，引入Logistic变换

$L\left( p \right) =\log \left[ {{p}/{\left( 1-p \right)}} \right]$

则

$L\left( s|z_{1:t} \right) =L\left( s|z_t \right) +L\left( s|z_{1:t-1} \right)$

称为栅格状态的更新模型。更新模型中与新测量值 $z_t$ 有关的项是 $L\left( s|z_t \right)$ ，由于激光雷达的测量值只有两种情况，因此定义

$\begin{cases} \mathrm{looccu}: L\left( s|z_t=1 \right)\\ \mathrm{lofree}: L\left( s|z_t=0 \right)\\\end{cases}$

必须指出， $\mathrm{looccu}$ 与 $\mathrm{lofree}$ 表达了在获得感知数据的情况下栅格真实状态的概率，这是与传感器性能有关的常数。传感器性能越好，测量结果越接近真实值， $\mathrm{looccu}$ 越大 $\mathrm{lofree}$ 越小。一般地，可以设定 $\mathrm{looccu}=0.9$ 、 $\mathrm{lofree}=-0.7$

2.2 截断策略

从更新模型可以看出， $L\left( s|z_{1:t} \right)$ 是对历史观测序列的整合。换言之，若假设 $\left| \mathrm{looccu} \right|=\left| \mathrm{lofree} \right|$ ，则当一个栅格被观察到 $k$ 次自由状态后，必须再被观察到至少 $k$ 次占据状态，才有可能被设置为占据栅格。这导致实际应用时，动态环境中的地图可能无法被快速更新。

为了建图的适应性，采用截断策略，定义概率上下限来限制改变栅格状态所需的更新次数，代价是概率在0-1区间内不再完备，靠近边界的概率丢失

$L\left( s|z_{1:t} \right) =\max \left\{ \min \left\{ L\left( s|z_t \right) +L\left( s|z_{1:t-1} \right) , L_{\max} \right\} , L_{\min} \right\}$

3 仿真实现

3.1 算法流程

算法流程如下所示

在这里插入图片描述
其中关于Bresenham视线法原理，请参考路径规划 | 图解Theta*算法(附ROS C++/Python/Matlab仿真)

3.2 Matlab实现

核心代码如下所示

for i = 1:N 
    x = scan_pose(1, i);
    y = scan_pose(2, i);
    theta = scan_pose(3, i);
    robot_pos = [ceil(x * resolution) + origin(1), ceil(y * resolution) + origin(2)];

    % Find grids hit by the rays (in the gird map coordinate)
    rays = scan_ranges(:, i);
    x_occ = rays .* cos(scan_angles + theta) + x;
    y_occ = -rays .* sin(scan_angles + theta) + y;
    occ_pos = [ceil(x_occ * resolution) + origin(1), ceil(y_occ * resolution) + origin(2)];

    % Find occupied-measurement cells and free-measurement cells
    occ_id = sub2ind(size(grid_map), occ_pos(:, 2), occ_pos(:, 1));

    free = [];
    for j = 1:scans_num
        [ix_free, iy_free] = bresenham(robot_pos, occ_pos(j, :));  
        free = [free; iy_free, ix_free];
    end
    free_id = sub2ind(size(grid_map), free(:, 1), free(:, 2));

    % Update the log-odds
    grid_map(occ_id) = grid_map(occ_id) + lo_occ;
    grid_map(free_id) = grid_map(free_id) - lo_free;

    % Saturate the log-odd values
    grid_map(grid_map > lo_max) = lo_max;
    grid_map(grid_map < lo_min) = lo_min;
end