Review

Cache Struct

• A cache is a set of $2^s$ cache sets
• A cache set is a set of E cache lines
  • if E=1, it is called “direct-mapped”
• Each cache line stores a block
• Total Capacity = S * B * E

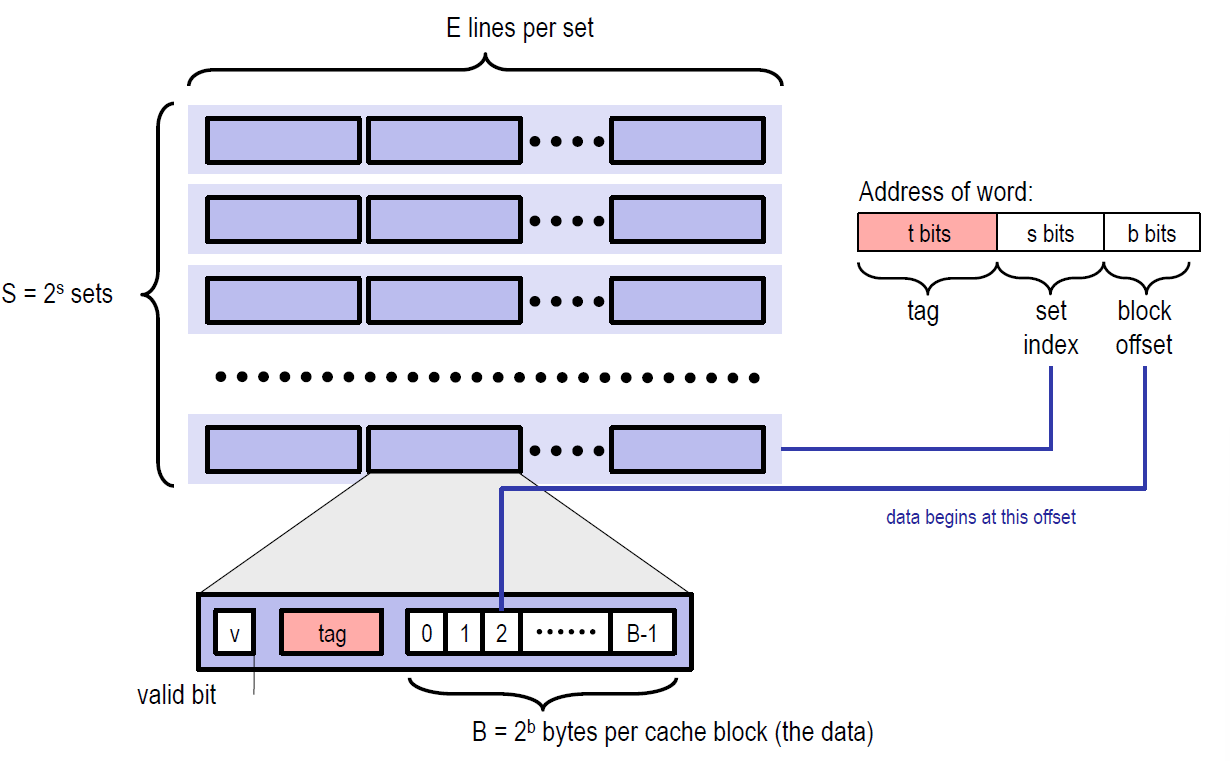
由此，我们可以写出cache line和cache的结构：

typedef struct cache_line{
    unsigned valid;
    int tag;
    int lru_cnt;
}cache_line;

cache_line **cache; // cache_line *cache[];

cache[s][e]表示cache的第s组的第e行

Types of Cache Misses

• Cold (compulsory) miss
  • 一个空的缓存对于任何数据的access都不会命中，此类不命中称为强制性不命中（compulsory miss）或冷命中（cold miss）
• Conflict miss
  • 因为第k层的capacity一定是小于第k+1层的，根据cache所采用的placement policy可知，第k+1层的block映射到第k层的block时一定会存在重复映射的情况，这种造成的miss称为冲突不命中（conflict miss）
• Capacity miss
  • 程序通常是按照一系列阶段来运行的，每个阶段访问缓存块的某个相对稳定不变的集合。例如，一个嵌套的循环会反复访问同一个数组的元素。这个块的集合会被称为这个阶段的工作集。当工作集的容量超过缓存的大小时，缓存会经历容量不命中（capacity miss）

Policy

• Placement policy
  • 只要发生了不命中，第k层的cache就把必须执行某个放置策略（Placement policy），来决定把它从第k+1层取出来的block放置何处。
  • 通常cache是使用的是严格的Placement policy，即由地址中的tag和set index两部分的位模式来决定其放置的位置，set index决定其放于哪个组set，tag决定其放于该set中的哪一行line
• Replacement policy
  • 如何第k层的缓存已经满了，此时又需要从第k+1层取新的块时，那么就需要决定该替换哪个块，这就又Replacement policy来决定
  • 常见的策略有FIFO、LRU、LFU和随机替换策略，FIFO就是先进来的先出去，LRU则会将最近一段时间未使用的数据evict，LFU将最近一段时间使用次数较少的数据evict，随机替换就会随机evict一个块

cache类型

1. **直接映射高速缓存(direct-mapped)：**E=1,S != 1

   根据[set index]确定数据所要存放的组别set，因为每个set只有一行，所以如果为空，则放，不为空则evict原数据

   该缓存tag位的意义不太，并不需要标记具体的行，但它可以用来记录confict miss

2. **组相联高速缓存：**E != 1, S != 1

   根据[set index]确定数据所要存放的组别set，因为每个set有E行，如果有空的行，则放进任意空行；如果没有空行，则根据replacement policy来确定被evict的行，

3. **全相联高速缓存：**E != 1 , S = 1

   该缓存因为S=1，所以对数据的位解释上就没有[set index]，只有tag和block offset；因此就直接根据tag来进行match

cache set中的each line并不是按照顺序来存储，而是利用键值对（key，value）来进行match，key是由有效位+tag位组合的

PartA

完成一个模拟cache需要按照以下步骤来：

先贴出全局变量

int hit=0,miss=0,evict=0;
int s,E,b,t;
// 用于提取set tag block offset的掩膜
int cover=1;
int row,col;

1. 读取s，E，b作为构建cache的三元组

   需要使用 getopt 函数来解析命令行参数，解析过程如下：

   // 所需的头文件
   #include <getopt.h>
   #include <stdlib.h>
   #include <unistd.h>
   
   while((opt = getopt(argc, argv, "s:E:b:t:")) != -1) {
       switch (opt)
       {
           case 's':
               s = atoi(optarg);
               break;
           case 'E':
               E = atoi(optarg);
               break;
           case 'b':
               b = atoi(optarg);
               break;
           case 't':
               pFile =fopen(optarg, "r");
               break;
           default:
               printf("unknown argument\n");
               exit(0);
               break;
       }
   }
   

2. 构建cache并且初始化

   typedef struct cache_line{
       unsigned valid;
       int tag;
       int lru_cnt;
   }cache_line;
   
   cache_line** create_cache()
   {
       row = pow(2,s);
       col = E;
       cache_line** cache = (cache_line **)malloc(sizeof(cache_line*)*row);
       int i;
       for(i=0; i<row; i++) 
           cache[i] = (cache_line *)malloc(sizeof(cache_line)*col);
       return cache;
   }
   
   void initial(cache_line** cache)
   {
       t = 64-b-s;
       for(int i=0; i<(b+s-1); i++) {
           cover<<=1;
           cover+=1;
       } 
       for(int i=0; i<row; i++)
           for(int j=0; j<col; j++) {
               cache[i][j].valid = 0;
               cache[i][j].tag = 0;
               cache[i][j].lru_cnt = 0;
           }
   }
   

3. 读取valgrind生成的trace文件，并且一条条执行命令，有三种命令

   • M（Modify）：写分配+写回，先从cache中读，再写
   • L（Load）：读取，从cache读数据，没有读到就直接写（这个store就一样了）
   • S（Store）：存储，向cache中写数据

   因为并没有涉及到真正的数据写或存储，并不关心数据是什么，只关注与读或者写时的miss，hint和evict情况。

   我们写一个load函数，其作用就是从cache去读数据(Load)，如果没有就写(Store)，所以M命令对应2次load函数，L命令对应一次load函数，S命令也对应一次load函数

   char identifier;
   unsigned address;
   int size;
   int cnt=1; 	// 用cnt记录数据最后的访问时间，越小表示上次访问已经过去很久了
   while(fscanf(pFile, "%c %x,%d",&identifier, &address, &size) > 0)
   {
       switch (identifier) 
       {
           case 'L':
               load(cache,address,size,cnt);
               break;
           case 'S':
               load(cache,address,size,cnt);
               break;
           case 'M':
               load(cache,address,size,cnt);
               load(cache,address,size,cnt);
               break;
           default:
               break;
       }
       cnt++;
   }
   

   load函数的实现如下：

   void load(cache_line** cache, unsigned address, int size, int _time)
   {
       int tag = address>>(b+s);
       int set = (address&cover)>>b;
       for(int j=0; j<col; j++) {
           if(cache[set][j].valid && (cache[set][j].tag == tag)) {
               hit++;
               cache[set][j].lru_cnt = _time;
               return;
           }
           if(cache[set][j].valid == 0) {
               miss++;
               cache[set][j].valid = 1;
               cache[set][j].tag = tag;
               cache[set][j].lru_cnt = _time;
               return;
           }
       }
       // 没有找到并且set内的所有line都满了
       // 找到没有使用时间最长的数据 将它evict掉
       int index=0;
       for(int j=0; j<col; j++) {
           if(cache[set][j].lru_cnt < cache[set][index].lru_cnt)
               index = j;
       }
       cache[set][index].tag = tag;
       cache[set][index].lru_cnt = _time;
       evict++;
       miss++;
       return;
   }
   

4. 输出记录的hint，miss和evict，并且释放cache和打开文件的的空间

printSummary(hit, miss, evict);
fclose(pFile);
free_cache(cache);

void free_cache(cache_line** cache)
{
    int row = pow(2,s);
    for(int i=0; i<row; i++)
        free(cache[i]);
}

完整的代码可以从我的github仓库获取

Part B

我们所写的转置代码在参考cache下运行（s = 5, E = 1, b =5）

实验讲义中允许我们可以针对特定形状的矩阵写出具有针对性的代码来降低miss率

我们先以矩阵乘法为例，讨论矩阵分块是如何对降低cache miss率的：

1. **分块乘法的正确性：**对于矩阵C=矩阵A*矩阵B，三个矩阵都是32x32，我们可以通过将每个矩阵分成16x16的四个小矩阵：

   

   C0中的元素C[0][0]仍然等于A0中的蓝块*B0中的蓝块 + A1中的绿块 *B2中的绿块；这等价于A0与A1组成的一行乘以B0和B2组成的一列

   分块矩阵乘法的代码：

   

   这段代码是由2个三重循环组成的6重循环，外三层是整体矩阵乘法i,j索引矩阵C的每个分块，k索引矩阵A和矩阵B相对应的分块组，例如A0和B0，A1和B2；内三层循环是分块内部的矩阵乘法，即在这部分落实每个元素的运算，i1,j1索引矩阵C当前分块的单个元素，k1索引k索引的分块组中相对应的元素。

2. **分块矩阵对命中率的提升：**我们假设矩阵的大小为n * n，cache block = 8。

   • 不分块：再假设cache的容量C远小于n，也就是说整个cache连矩阵的一行都装不下，每一次重新读一行必定miss

     对于矩阵A来说，是行读取，步数为1，每个block的第一个元素会miss，后面7个都会hint，即每8个元素miss一次，一行n个元素，miss $n/8$ 次；

     对于矩阵B来说，是列读取，步数为n，因为$C<<n$，即使用完cache的每个组后，也不会读完所有行，然后新的行又会覆盖原来的block，所以矩阵B每次读都不会命中，一列n个元素，miss $n$ 次；即对计算矩阵C的一个元素总共miss $(9n)/8$，一共$n^2$个元素，所以一共miss $(9n^3)/8$。（注意这里咱不考虑A和B的重复覆盖和读取C的miss，下面分块也是）

     

   • 分块：再假设分块的大小B * B（B<=8），cache的容量C远小于n，但是能容下3个分块大小，$3B^2<C$，可以放下A，B，C三个矩阵的方块

     对于矩阵A的方块来说，步数为1已经为最佳状态，还是每个block的第一个元素会miss，分块内一行B个元素，所以一行miss $B/8$ 次，一个分块B行，即一个分块miss $B^2/8$次；

     对于矩阵B来说，因为cache可以放下完整的一个分块，所以不会存在读取新的一行时覆盖原来的block的这种浪费情况，也就是说矩阵分块解决了矩阵内部相互覆盖的问题，在读完第一列都不命中后，读取第二列，第三列…到第B列，每个元素都已经缓存在cache中，都会hint，即整个分块的miss次数为$B^2/8$次！矩阵B和矩阵A在分块后每块的miss率一致

     计算矩阵C的一个分块，需要读取$n/B$个矩阵A分块和矩阵B分块，即计算矩阵C一个分块miss$\frac{2n}{B}\ast \frac{B^2}{8}=\frac{nB}{4}$次。矩阵C共有${\frac{n}{B}}^2$个分块，即总miss次数为：

     $$\frac{nB}{4}\times {\frac{n}{B}}^2=\frac{1}{4B}{n}^2$$

     

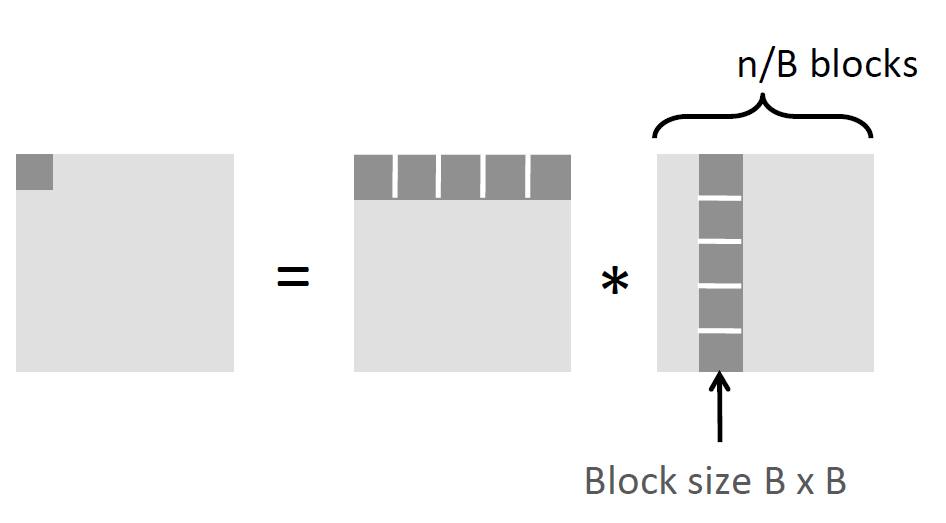
   经过上面的分析得知，分块对提升命中率的几点信息：

   1. $3B^2<C$，即cache的容量需要放下3个分块的大小
   2. 分块对矩阵乘法命中率的提升是通过降低矩阵B的miss次数达到的

在介绍完矩阵分块乘法的前置知识后，回到本次lab的partB部分：

根据给出的cache参数，s=5，E=1，b=5，可以得知该cache是一个有$2^5=32$个组，每组只有一行，每一行的block大小为$2^5=32$个字节，可以存下8个int的直接映射高速缓存：

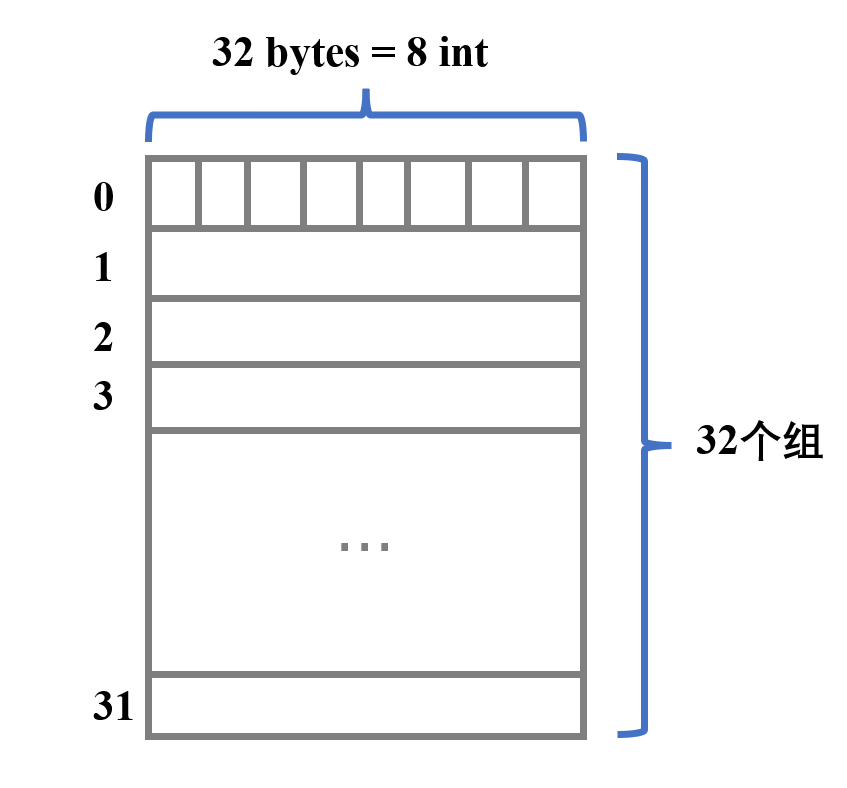
partB不是提高矩阵乘法的命中率，而是提高矩阵转置的命中率，即只有两个矩阵A和B参与。
我们假设是将矩阵A进行转置，存储到矩阵B上：

• 矩阵转置下不分块：和矩阵乘法部分一样，矩阵A一行不命中$\frac{n}{8}$次，矩阵A的一行对应于目标矩阵B的一列（这里我们考虑读取目标矩阵的miss），矩阵B一列全不命中，为$n$次，所以转置矩阵A的一行不命中$\frac{9n}{8}$次，转置整个矩阵不命中$\frac{9n}{8}\times n=\frac{9}{8}{n}^2$次。
• 矩阵转置分块：和矩阵乘法部分一样，矩阵A和矩阵B的不命中次数一样，都是$\frac{B^2}{8}$，即转置一个方块的的不命中次数为$\frac{B^2}{4}$，总共有${\frac{n}{B}}^2$个方块，即转置整个矩阵，总miss次数为$\frac{1}{4}{n}^2$（这个结论我不敢保证其正确性，我只是需要算出一共理论最少的miss次数，供优化参考，如果有正确的值如果能告知我我将万分感激）。

trans.c中给出了暴力解法的代码，可以供我们作为对比进行优化：

void trans(int M, int N, int A[N][M], int B[M][N])
{
    int i, j, tmp;
    for (i = 0; i < N; i++) {
        for (j = 0; j < M; j++) {
            tmp = A[i][j];
            B[j][i] = tmp;
        }
    }    
}

下面是实验要求，Let’s go!

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JCjzOfg2-1671357441384)(null)]

32 x 32

对于分块优化命中率，最重要的问题就是确定分块Block的大小，却决于3个size：

1. cache block size（8个int）
2. cache size（32x8个int）
3. input cache size （32x32）

分块大小B设置的太大，如果超过了cache block的大小，那么对列模式的矩阵B来说miss，并且我们的缓存只够存矩阵的8行，如果分块超过8就意味着矩阵内的重叠；设置的太小，也会增加矩阵B的miss次数，缓存的资源被浪费。对于32x32，我们对其分成16个8x8的分块，转置代码如下：

void transpose_submit(int M, int N, int A[N][M], int B[N][M])
{
	for(int i=0; i<N; i+=8)
        for(int j=0; j<M; j+=8)
            for(int i1=i; i1<i+8；i1++)
                for(int j1=j; j1<j+8; j1++)
                    B[j1][i1] = A[i1][j1];
}

得到的结果如下：

miss次数为343次，没有拿到满分，根据我们之前推到的公式来看，32x32矩阵，分块后的最少不命中次数应该是$\frac{1}{4}\times 32^2=256$次，很明显还有我们没有考虑到的地方有多余的miss。

我们在计算公式时，对其进行了理想化处理，即不考虑矩阵A和矩阵B的重叠问题。但在实际情况中这是大量存在的，对于矩阵的大小是缓存大小的倍数时，两个相同大小的矩阵，在缓存进cache时相同位置是会产生冲突的。例如本例中，32x32矩阵是32x8大小的cache的4倍。

对于矩阵转置的情况下，除了对角线上的块，其他的块不会出现重叠的部分。

本例中，各个元素在缓存中的映射关系如下（图源）：

矩阵转置下的冲突情况：

A中标红的块占用的是缓存的第 0，4，8，12，16，20，24，28组，而B中标红的块占用的是缓存的第2，6，10，14，18，16，30组，刚好不会冲突。

那么我们该如何解决对角线上的冲突？lab讲义中提到我们可以使用12个自定义变量，这个工具不能忘了，也就是说我们直接可以把A的每一行转置的元素转从到8个变量里，再存在B中，这就避免了对角线上的冲突。

代码如下：

for(int i=0; i<32; i+=8)
    for(int j=0; j<32; j+=8)
        for(int i1=i; i1<i+8; i1++)
        {
            int a1 = A[i1][j];
            int a2 = A[i1][j+1];
            int a3 = A[i1][j+2];
            int a4 = A[i1][j+3];
            int a5 = A[i1][j+4];
            int a6 = A[i1][j+5];
            int a7 = A[i1][j+6];
            int a8 = A[i1][j+7];

            B[j][i1] = a1;
            B[j+1][i1] = a2;
            B[j+2][i1] = a3;
            B[j+3][i1] = a4;
            B[j+4][i1] = a5;
            B[j+5][i1] = a6;
            B[j+6][i1] = a7;
            B[j+7][i1] = a8;
        }

结果如下：

64x64

根据公式所得最小不命中次数为$\frac{1}{4}\times 64^2=1024$次，我们讨论分块大小该怎么设置：变大后的矩阵，原来的缓存只够存下4行，如果分块超过4行，那么矩阵内部就会出现重叠。那我们先采取4x4的分块，并且进行对角线优化，代码如下:

for(int i=0; i<64; i+=4)
    for(int j=0; j<64; j+=4)
        for(int i1=i; i1<i+4; i1++)
        {
            int a1 = A[i1][j];
            int a2 = A[i1][j+1];
            int a3 = A[i1][j+2];
            int a4 = A[i1][j+3];


            B[j][i1] = a1;
            B[j+1][i1] = a2;
            B[j+2][i1] = a3;
            B[j+3][i1] = a4;
        }

得到的结果如下:

1699次，还没有到达满分，但相比不分块的4723次已经有很大的提升了！

如果进一步缩小分块大小，显然会出现资源浪费导致的miss次数上升，而增大分块大小，也会因矩阵内重叠导致miss上升，但是放大比缩小有更多的操作空间，还可以分块内再分块。

我们考虑将分块大小增大到8x8，再在每个8x8的分块内分成4个4x4个分块，这样就能避免因为因为块增大而带来的矩阵内重叠。对于4x4分块带来的问题是缓存利用率不高，为此我们需要用点技巧来提高其利用率：

读取矩阵A时，会缓存A0、A1两个4x4的分块，如果只是单纯的4x4分块中，A1的缓存是会被浪费的，在这里为了充分利用缓存，我们把A1也存到矩阵B中相同位置上，但我们知道这个位置是错误的，所以用本地变量把此时矩阵B分块的右上角的4x4分块存起来。

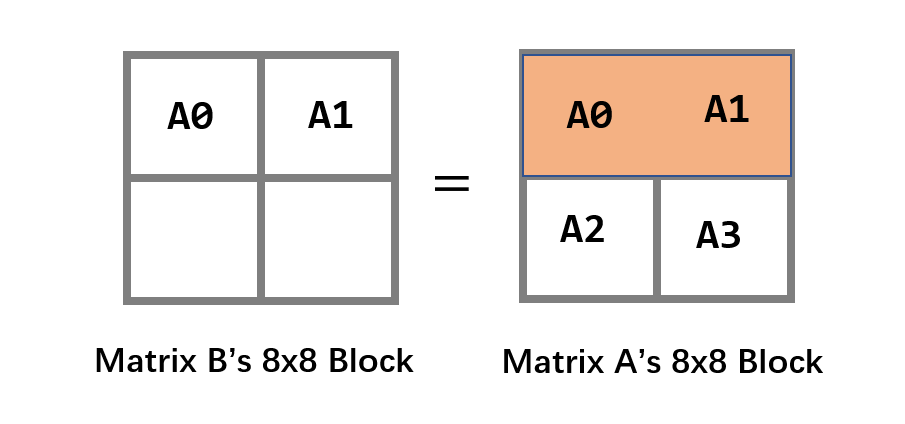
在写完矩阵B分块第一行后：

1. 此时cache内缓存着矩阵B分块的第一行，我们利用缓存将矩阵B右上角写入本地变量中

2. 此时我们读矩阵A的A2和A3（分块第二行）时，不会和矩阵B分块的第一行冲突覆盖。将A2块，复制到矩阵B分块的右上角，并且顺便将A3块存进本地变量。

3. 在访问矩阵B左下角时，把之前存储的本地变量中的A1和A3复制进去。

   这样的顺序才能达到缓存的最大利用效果，示意图如下：

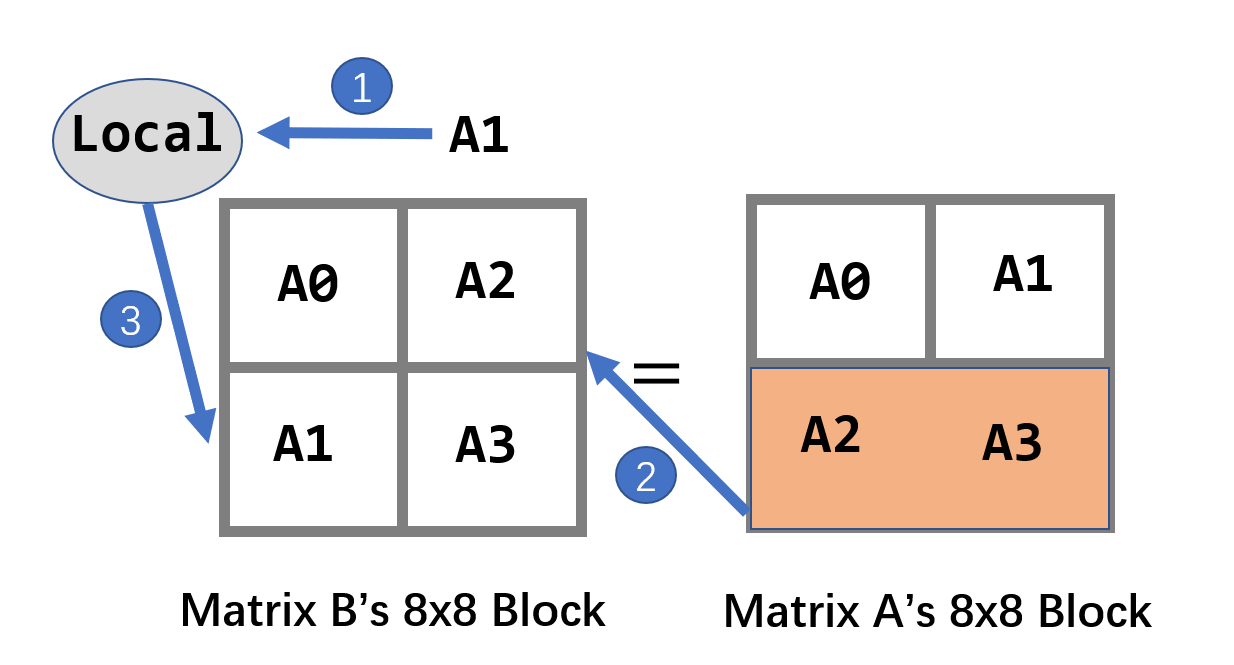
转置代码如下：

int a1,a2,a3,a4,a5,a6,a7,a8,a9,a10,a11,a12;
// 遍历矩阵A的每个8x8的分块
for(int i=0; i<64; i+=8)
    for(int j=0; j<64; j+=8){
        // Step1：将A0 A1转给B0 B1
        for(int k=i; k<i+4; k++){
            a1 = A[k][j];
            a2 = A[k][j+1];
            a3 = A[k][j+2];
            a4 = A[k][j+3];
            a5 = A[k][j+4];
            a6 = A[k][j+5];
            a7 = A[k][j+6];
            a8 = A[k][j+7];

            B[j][k] = a1;
            B[j+1][k] = a2;
            B[j+2][k] = a3;
            B[j+3][k] = a4;
            B[j+0][k+4] = a5;
            B[j+1][k+4] = a6;
            B[j+2][k+4] = a7;
            B[j+3][k+4] = a8;
        }
        for(int k=j; k<j+4; k++){
            // 复制矩阵B右上角分块到local
            a1 = B[k][i+4];
            a2 = B[k][i+5];
            a3 = B[k][i+6];
            a4 = B[k][i+7];
            // 把矩阵A左下角分块A2复制到矩阵B右上角分块
            a5 = A[i+4][k];
            a6 = A[i+5][k];
            a7 = A[i+6][k];
            a8 = A[i+7][k];
			// 顺便将矩阵A右下角存进本地变量
            a9 = A[i+4][k+4];
            a10 = A[i+5][k+4];
            a11 = A[i+6][k+4];
            a12 = A[i+7][k+4];

            B[k][i+4] = a5;
            B[k][i+5] = a6;
            B[k][i+6] = a7;
            B[k][i+7] = a8;
            // 把local复制到矩阵B分块的第二行
            B[k+4][i] = a1;
            B[k+4][i+1] = a2;
            B[k+4][i+2] = a3;
            B[k+4][i+3] = a4;		
            B[k+4][i+4] = a9;
            B[k+4][i+5] = a10;
            B[k+4][i+6] = a11;
            B[k+4][i+7] = a12;
        }
    }

测试结果如下：

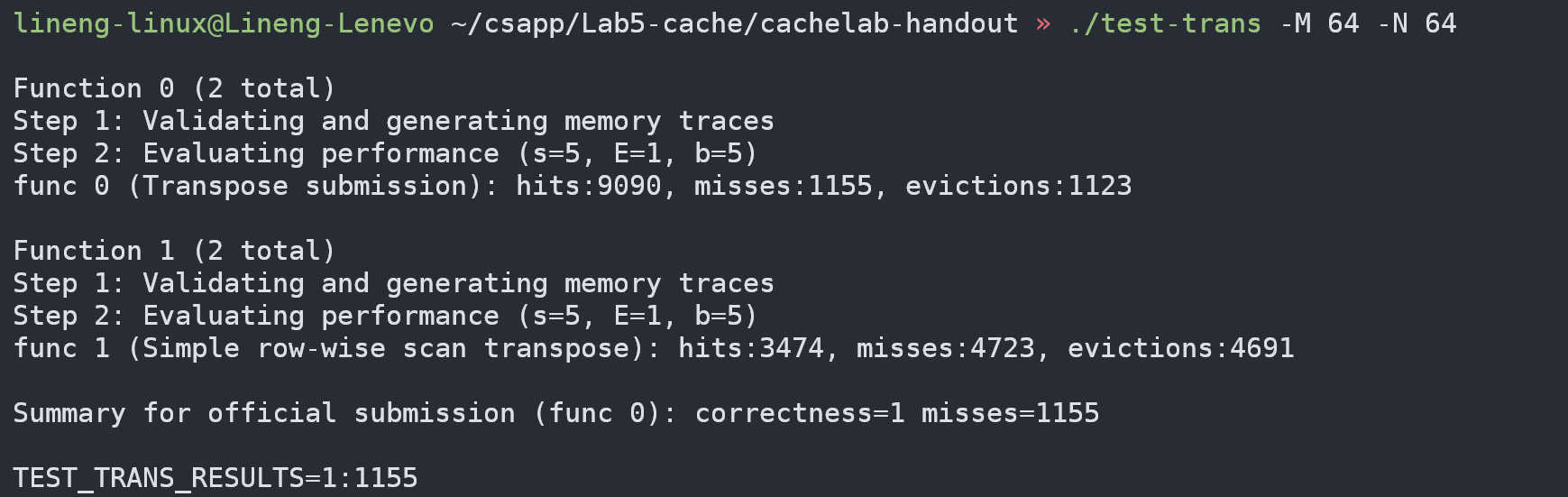
1155次，成功！

61x67

对于该不规则的矩阵，需要留意在两层内层循环中多加上一个判断条件：

• i1<N
• j1<M

这样就能把整个矩阵每个元素都清理一遍，lab对这个矩阵的miss次数要求比较低，通过一个16x16分块就能直接通过，代码如下：

for(int i=0; i<N; i+=16)
    for(int j=0; j<M; j+=16)
        for(int i1=i; i1<i+16 && i1<N; i1++)
            for(int j1=j; j1<j+16 && j1<M; j1++)
                B[j1][i1] = A[i1][j1];

测试结果如下：

1992次，成功！

Summary

到此，整个实验都已完成！