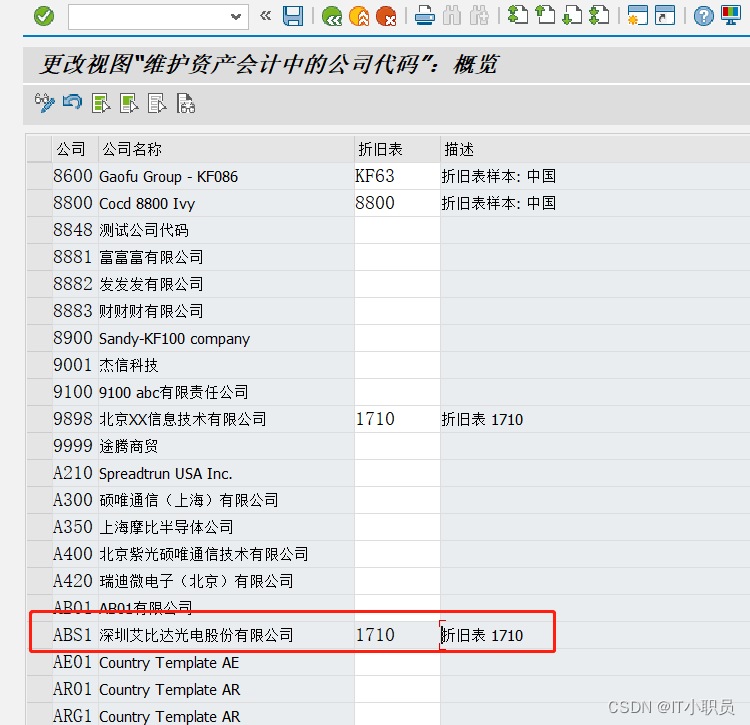
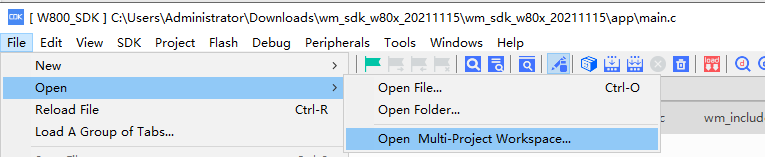
大整数相加
- 列竖式运算
- 第一步
- 第二步
- 第三步
- 第四步
- JAVA实现
给出两个很大的整数,要求实现程序求出两个整数之和。
记得这个题目我大二ACM课程老师讲过,但是忘记了。。。。。。。。。。
列竖式运算
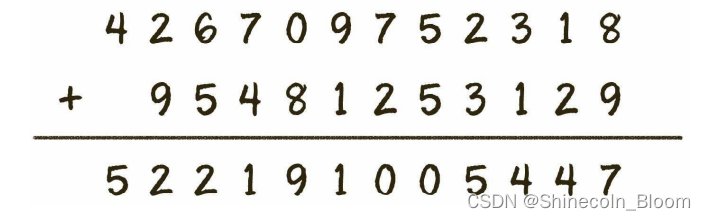
程序不可能通过一条指令计算出两个大整数之和,但我们却可以把大运算拆解成若干小运算,像小学生列竖式一样进行按位计算。
用数组存储大数:数组的每一个元素,对应着大整数的每一个数位。
第一步
创建两个整型数组,数组长度是较大整数的位数+1。
把每一个整数倒序存储到数组中,
整数的个位存于数组下标为0的位置,最高位存于数组的尾部。
之所以倒序存储,是因为这样更符合从左到右访问数组的习惯。
第二步
创建结果数组,结果数组的长度同样是较大整数的位数+1,
+1的目的是给最高位进位预留的。
第三步
遍历两个数组,从左到右按照对应下标把元素两两相加
第四步
把result数组的全部元素再次逆序,去掉首位的0(没有进位的情况),就是最终结果。
例子:
426 709 752 31 8 +95481 253 129
第一步
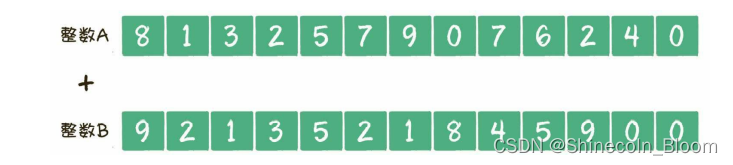
第二步
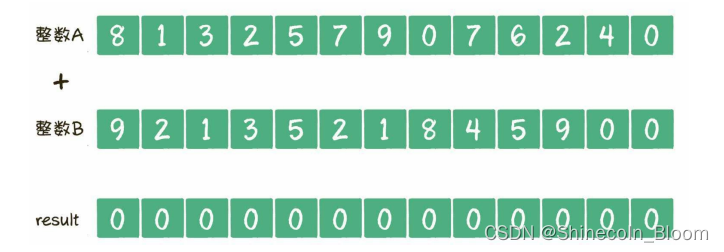
第三步


以此类推……一直把数组的所有元素都相加完毕。
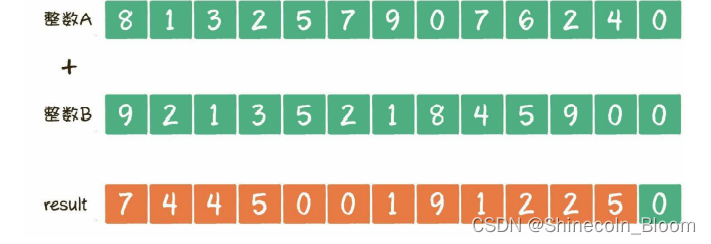
第四步

JAVA实现
利用加‘0’和减‘0’完成char和int相互转换:JAVA中char转int小Tips
/**
* 大整数求和
* @param bigNubmerA 大整数A
* @param bigNumberB 大整数B
* @return
*/
public static String bigNumberSum(String bigNubmerA,String bigNumberB){
//1.把两个大整数用数组逆序存储,数组长度等于较大整数位数+1
int maxLength = bigNubmerA.length()>bigNumberB.length()?bigNubmerA.length():bigNumberB.length();
int[]arrayA = new int[maxLength+1];
int[]arrayB = new int[maxLength+1];
for (int i=0;i<bigNubmerA.length();i++){
//为了符合正常逻辑,数组的低位存储大数的低位
arrayA[i] = bigNubmerA.charAt(bigNubmerA.length()-1-i)-'0';
}
for (int a:arrayA){
System.out.print(a);
}
System.out.println();
for (int i=0;i<bigNumberB.length();i++){
//为了符合正常逻辑,数组的低位存储大数的低位
arrayB[i] = bigNumberB.charAt(bigNumberB.length()-1-i)-'0';
}
for (int b:arrayB){
System.out.print(b);
}
System.out.println();
//2.构建result数组,数组长度等于较大整数位数+1
int[] result = new int[maxLength+1];
//3.遍历数组,按位相加
for (int i = 0;i<result.length;i++){
int temp = result[i];
temp = temp+arrayA[i];
temp = temp+arrayB[i];
//判断是否进位
if(temp>9){
//进位操作
temp = temp-10;
result[i+1] = 1;
}
result[i] = temp;
}
//4.把result数组再次逆序并转成String
StringBuffer sb = new StringBuffer();
//是否找到大整数的最高有效位
boolean findFirst = false;
//从result高位开始遍历
//应为result高位就是实际数字的低位
for (int i= result.length-1;i>=0;i--){
if(!findFirst){
if(result[i]==0){
//说明高位是0,就再次循环,直到result[i]!=0时,才跳出
continue;
}
findFirst = true;
}
//到这一步,说明已经找到了非0最高位,就直接append就行
sb.append(result[i]);
}
return sb.toString();
}
测试方法:
public static void main(String[] args) {
System.out.println(bigNumberSum("426709752318","95481253129"));
}
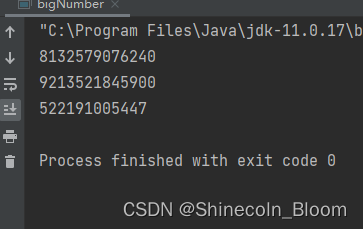
这里为了方便存储数据查看,我以200+300为例子:
关键在于第四步代码需要注意
如何找到result的最高位,并开始遍历。。
借助findFirst标记和循环、continue
//4.把result数组再次逆序并转成String
StringBuffer sb = new StringBuffer();
//是否找到大整数的最高有效位
boolean findFirst = false;
//从result高位开始遍历
//应为result高位就是实际数字的低位
for (int i= result.length-1;i>=0;i--){
if(!findFirst){
if(result[i]==0){
//说明高位是0,就再次循环,直到result[i]!=0时,才跳出
continue;
}
findFirst = true;
}
//到这一步,说明已经找到了非0最高位,就直接append就行
sb.append(result[i]);
}