代码随想录算法训练营第十八天|513. 找树左下角的值|112. 路径总和|106. 从中序与后序遍历序列构造二叉树

513. 找树左下角的值

题目：给定一个二叉树的根节点 root，请找出该二叉树的最底层最左边节点的值。
假设二叉树中至少有一个节点。

示例 1: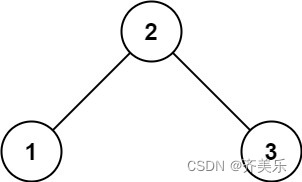 请添加图片描述

输入: root = [2,1,3]
输出: 1

思路一：层序遍历，最后一层的第一个元素，即是树左下角的值。
思路二：通过递归，深度优先遍历原则，因为本题没有中间节点的处理逻辑，所以使用前、中、后序遍历都可以，保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值

思路一：层序遍历
C#代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int FindBottomLeftValue(TreeNode root) {
        var result = 0;
        if(root == null) return result;
        var queue = new Queue<TreeNode>();
        queue.Enqueue(root);
        while(queue.Any()){
            int len = queue.Count;
            var itemList = new Queue<int>();
            while(len>0){
                var temp = queue.Dequeue();
                itemList.Enqueue(temp.val);
                if(temp.left!=null) queue.Enqueue(temp.left);
                if(temp.right!=null) queue.Enqueue(temp.right);
                len--;
            }
            result = itemList.Dequeue();
        }
        return result;
    }
}

思路二：递归
C#代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    //结果值
    int result = 0;
    //最大深度
    int maxDepth = -1;
    public int FindBottomLeftValue(TreeNode root) {
        Traversal(root,1);
        return result;
    }
    // 1. 确定返回值和参数
    public void Traversal(TreeNode node,int depth){
        //2. 确定终止条件
        if(node.left==null&&node.right== null){
            //叶子节点
            if(depth>maxDepth){//当前深度大于最大深度
                maxDepth = depth;//记录当前深度为最大深度
                result = node.val;
            }
        }
        //找左下角的值所以优先遍历左左子树
        if(node.left!=null){
            depth++;
            Traversal(node.left,depth);
            //回溯深度的值
            depth--;
            //精简代码 traversal(root->left, depth + 1);  隐藏着回溯
        }
        //遍历右子树
        if(node.right!=null){
            depth++;
            Traversal(node.right,depth);
            depth--;
        }
    }
}

112. 路径总和

题目：给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点是指没有子节点的节点。
示例一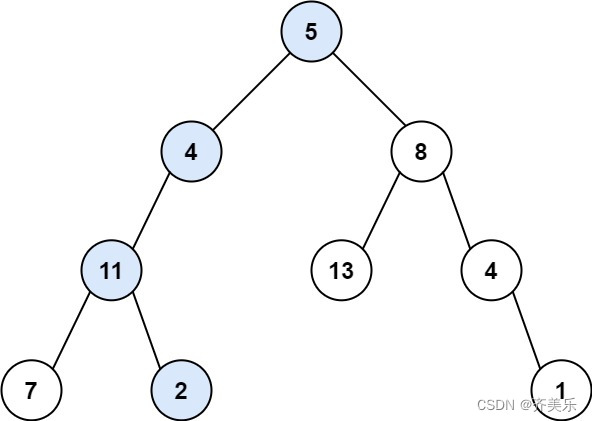：请添加图片描述

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

思路：可以使用深度优先遍历的方式（本题前中后序都可以，无所谓，因为中节点也没有处理逻辑）来遍历二叉树

C#代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public bool HasPathSum(TreeNode root, int targetSum) {
        if(root == null) return false;
        targetSum -= root.val;
        //确定终止条件
        if(root.left == null && root.right == null){
            return targetSum == 0;
        }
        if(root.left!=null){
            if(HasPathSum(root.left,targetSum)) return true;
        }
        if(root.right!=null){
            if(HasPathSum(root.right,targetSum)) return true;
        }
        return false;
    }
}

113. 路径总和 II

题目：给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。

叶子节点是指没有子节点的节点。
示例一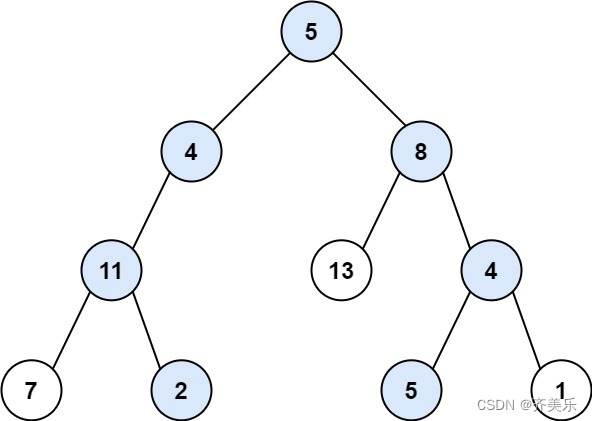：请添加图片描述

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

C#代码：

public class Solution {
    List<IList<int>> result = new List<IList<int>>();
    public IList<IList<int>> PathSum(TreeNode root, int targetSum) {
        var list = new List<int>();
        Traversal(root,targetSum,list);
        return result;
    }
    public void Traversal(TreeNode root, int targetSum,List<int> list){
        if(root == null) return;
        list.Add(root.val);
        targetSum -= root.val;
        //到达叶子节点并且路径正确
        if(root.left==null&&root.right==null&&targetSum==0){
            result.Add(new List<int>(list.ToArray()));
            return;
        }
        if(root.left!=null){
            Traversal(root.left,targetSum,list);
            //回溯
            list.RemoveAt(list.Count - 1);
        }
        if(root.right!=null){
            Traversal(root.right,targetSum,list);
            //回溯
            list.RemoveAt(list.Count - 1);
        }
    }
}

106. 从中序与后序遍历序列构造二叉树

题目：给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。
示例一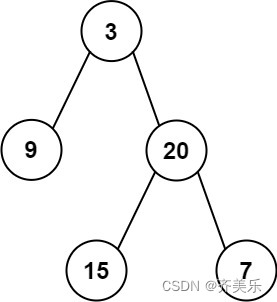：请添加图片描述

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

思路：

通过后序序列可以知道最后一个元素为根结点。
知道根结点后，通过中序序列可以判断出根结点的左右子树。

解题过程：

第一步：如果数组大小为零的话，说明是空节点了。
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组（顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

C#代码，递归

public class Solution {
    public TreeNode BuildTree(int[] inorder, int[] postorder) {
        // 1. 如果后序数组元素为0，则为空树
        if(postorder.Length==0) return null;
        // 2. 取后序序列的最后一个元素，得到根结点
        int rootVale = postorder[postorder.Length - 1];
        TreeNode node = new TreeNode(rootVale);
        if(postorder.Length == 1) return node;
        // 3. 通过根结点找到中序序列的分割点下标
        int index;
        for(index = 0; index<inorder.Length; index++){
            if(inorder[index] == rootVale){
                break;
            }
        }
        // 4. 分割左子树
        //左子树的中序序列
        int[] leftInorder = new int[index];
        //遍历拷贝
        // for(int i = 0;i<leftInorder.Length;i++){
        //     leftInorder[i] = inorder[i];
        // }
        //使用Array.Copy方法
        Array.Copy(inorder,0,leftInorder,0,leftInorder.Length);
        int[] leftPostorder = new int[leftInorder.Length];
        // for(int i= 0; i<leftPostorder.Length;i++){
        //     leftPostorder[i] = postorder[i];
        // }
        Array.Copy(postorder,0,leftPostorder,0,leftPostorder.Length);
        // 5. 分割右子树
        //右子树的中序序列
        int[] rightInorder = new int[inorder.Length -(index+1)];
        // for(int i = 0;i<rightInorder.Length;i++){
        //     rightInorder[i] = inorder[i+index+1];
        // }
        Array.Copy(inorder,index+1,rightInorder,0,rightInorder.Length);
        int[] rightPostorder = new int[rightInorder.Length];
        // for(int i = 0;i<rightPostorder.Length;i++){
        //     rightPostorder[i] = postorder[i+leftPostorder.Length];
        // }
        Array.Copy(postorder,leftPostorder.Length,rightPostorder,0,rightPostorder.Length);
        // 6. 递归左区间和右区间
        node.left = BuildTree(leftInorder,leftPostorder);
        node.right = BuildTree(rightInorder,rightPostorder);
        return node;
    }
}

105. 从前序与中序遍历序列构造二叉树

题目：给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。
示例一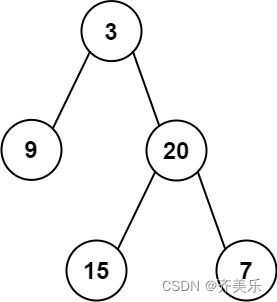：请添加图片描述

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

思路和后序遍历一样，通过前序遍历的第一个元素可知根结点，通过根结点和中序序列，分割出左右子树，通过递归即可构建出二叉树。

C#代码：

public class Solution {
    public TreeNode BuildTree(int[] preorder, int[] inorder) {
        //1. 判断前序遍历长度
        if(preorder.Length == 0) return null;
        //2. 获取根结点
        int rootVale = preorder[0];
        TreeNode root = new TreeNode(rootVale);
        if(preorder.Length == 1) return root;
        //3. 获取根结点在中序序列中的下标
        int index;
        for(index = 0;index<inorder.Length;index++){
            if(inorder[index] == rootVale){
                break;
            }
        }
        //4. 分割左子树
        int[] leftInorder = new int[index];
        Array.Copy(inorder,0,leftInorder,0,index);
        int[] leftPreorder = new int[leftInorder.Length];
        Array.Copy(preorder,1,leftPreorder,0,leftPreorder.Length);
        //5. 分割右子树
        int[] rightInorder = new int[inorder.Length -(index+1)];
        Array.Copy(inorder,index+1,rightInorder,0,rightInorder.Length);
        int[] rigthPreorder = new int[rightInorder.Length];
        Array.Copy(preorder,1+leftPreorder.Length,rigthPreorder,0,rigthPreorder.Length);
        //6. 递归左区间和右区间
        root.left = BuildTree(leftPreorder,leftInorder);
        root.right = BuildTree(rigthPreorder,rightInorder);
        return root;
    }
}