买卖股票的最佳时机含冷冻期

news2025/1/18 9:49:38

题目链接

买卖股票的最佳时机含冷冻期

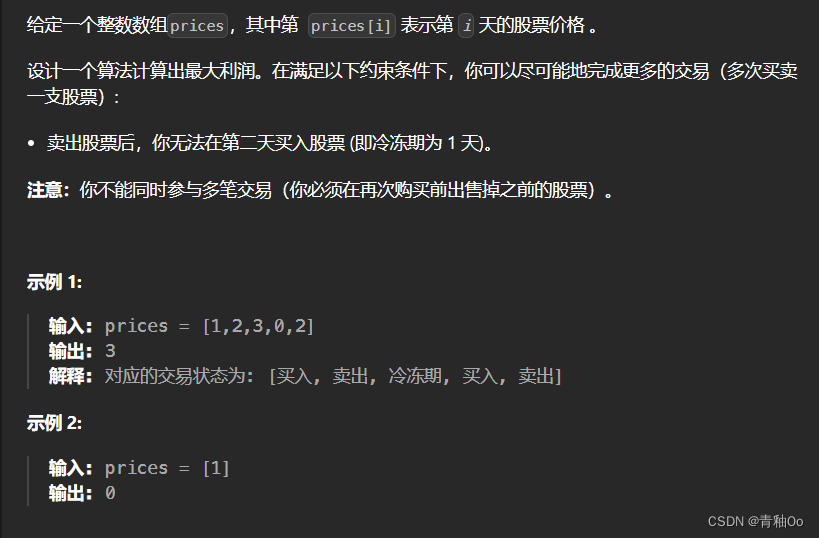
题目描述

注意点

卖出股票后，无法在第二天买入股票 (即冷冻期为 1 天)
不能同时参与多笔交易（必须在再次购买前出售掉之前的股票）
可以尽可能地完成更多的交易（多次买卖一支股票）
计算最大利润
0 <= prices[i] <= 1000

解答思路

最初想到的是深度优先遍历，通过买入、卖出、冷冻期、跳过操作四种状态深度搜索所有的情况，找到最大利润，但是最后超出时间限制
参照题解使用动态规划完成本题，用 f[i] 表示第 i 天结束之后的「累计最大收益」。根据题目描述，由于最多只能同时买入（持有）一支股票，并且卖出股票后有冷冻期的限制，因此会有三种不同的状态：
（1）目前持有一支股票，对应的「累计最大收益」记为 f[i][0]；
（2）目前不持有任何股票，并且处于冷冻期中，对应的「累计最大收益」记为 f[i][1]；
（3）目前不持有任何股票，并且不处于冷冻期中，对应的「累计最大收益」记为 f[i][2]。

代码

class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length == 0) {
            return 0;
        }
        int n = prices.length;
        /**
          * dp[i][0]对应第i天持有一支股票的累积最大收益（第i - 1天可能持有股票，也可能未持有第i - 1天才买入）
          * dp[i][1]对应第i天不持有股票且处于冷冻期的累积最大收益（第i - 1天必定卖出）
          * dp[i][2]对应第i天不持有股票且不处于冷冻期的累积最大收益（第i - 1天可能处于冷冻期，也可能不处于冷冻期）
         */
        int[][] dp = new int[n + 1][3];
        dp[0][0] = -prices[0];
        for (int i = 1; i <= n; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][2] - prices[i - 1]);
            dp[i][1] = dp[i - 1][0] + prices[i - 1];
            dp[i][2] = Math.max(dp[i - 1][1], dp[i - 1][2]);
        }
        return Math.max(dp[n][1], dp[n][2]);
    }
}