写在最前面

D题好熟悉，不就是2014C题的养猪变成养羊了吗hhhh
涉及：最优化算法（目标函数：问题2的出栏羊最多、问题3的期望损失最小）
不涉及excel的数据预处理
适合团队：建模能力较强
如果能抽象数学公式建模，适用lingo软件求解，非常方便

E题涉及excel的数据预处理

E题

最好先对excel的数据做异常值检测（四分位数、箱型图）+处理（线性填充）
问题1，折线图、热力图（相关性分析）、关联分析（可考虑）
问题2，题目直接点明：季节性——>ARIMA时间序列分析，注意先检测能否用ARIMA模型
问题3，问题2的模型，用于问题3求解，然后根据突变型、季节性等问题2的突变点来给监测方案（数据分析+文字建模）

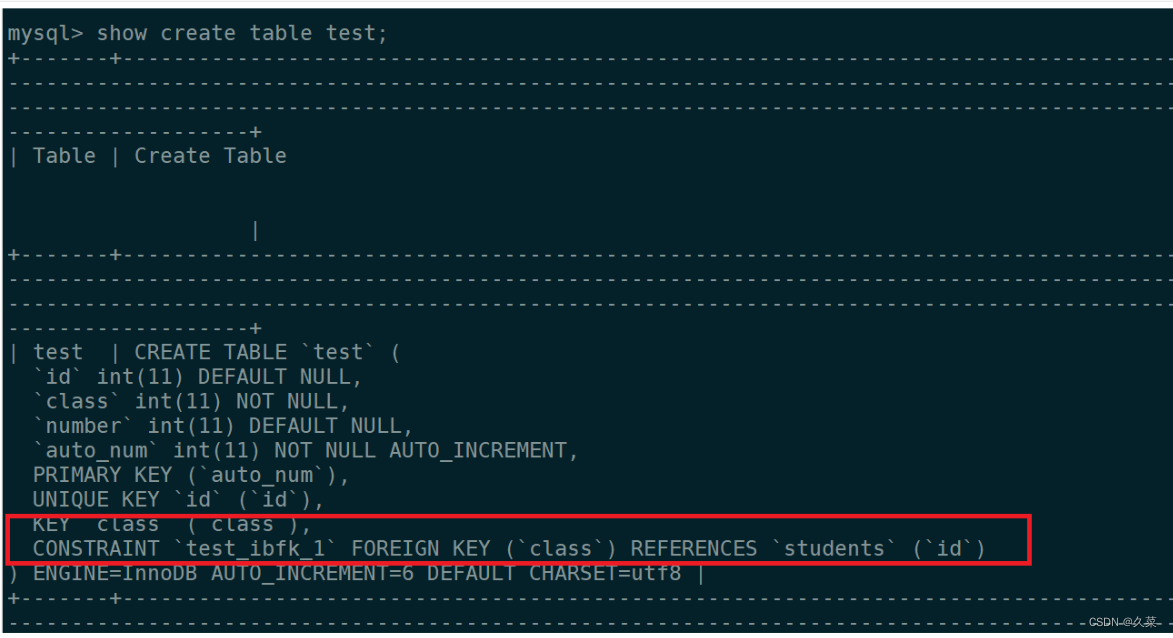
D题

可以画思维导图，帮助理清逻辑。

2014C题优秀论文笔记

下面是之前2014C题的优秀论文笔记。

1、结构清晰（后附该论文前两问的目录结构）
2、lingo求解优化模型，涉及函数循环与求和
3、表格很好看
4、关于sets，参考
https://blog.csdn.net/qq_47925836/article/details/119088653
5、代码和论文的结果没太明白，感觉优化过？

问题一（求解母猪年均产仔量以达到或超过盈亏平衡点）

盈亏平衡方程、多元函数建立计算模型、求解盈亏平衡问题

一、数据准备
1.搜集相关数据

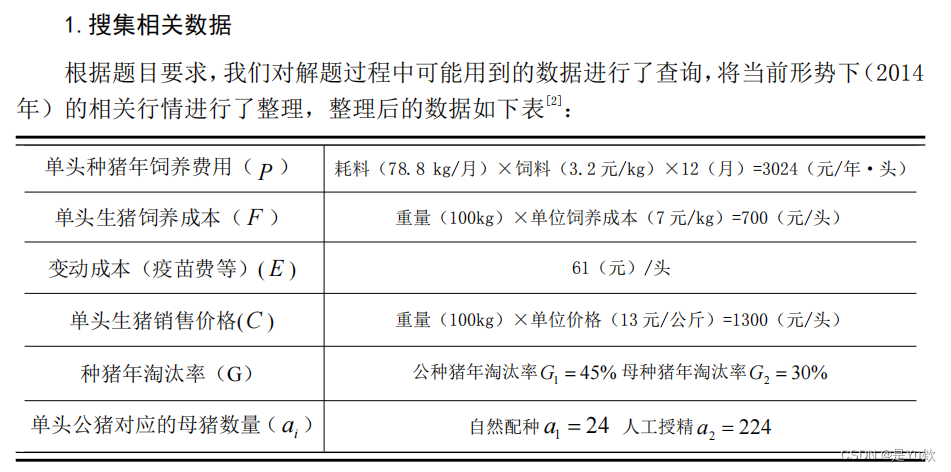
2.确定养殖周期

二、利用盈亏平衡分析法确定产仔量
1.求解养殖总成本
（1）种猪饲养成本
（2）后备种猪饲养成本
（3）生猪饲养成本
（4）变动成本
（5）总成本
2.求解总收入
3.根据盈亏平衡点求解产仔量

三、结果分析（亮点！！！）

在 2014 年养猪行情下，不论采取何种配种方式和养殖周期该养殖场均无法达到盈亏平衡，
因此我们分析，若该养殖场在前两年的猪市行情下进行养殖可能会达到盈亏平衡。
所以我们又对 2013 年和 2012 年的猪市行情进行了调查，利用这两年的养殖成本和销售价格等数据对该养殖场的盈亏平衡点和母猪年均产仔量进行求解

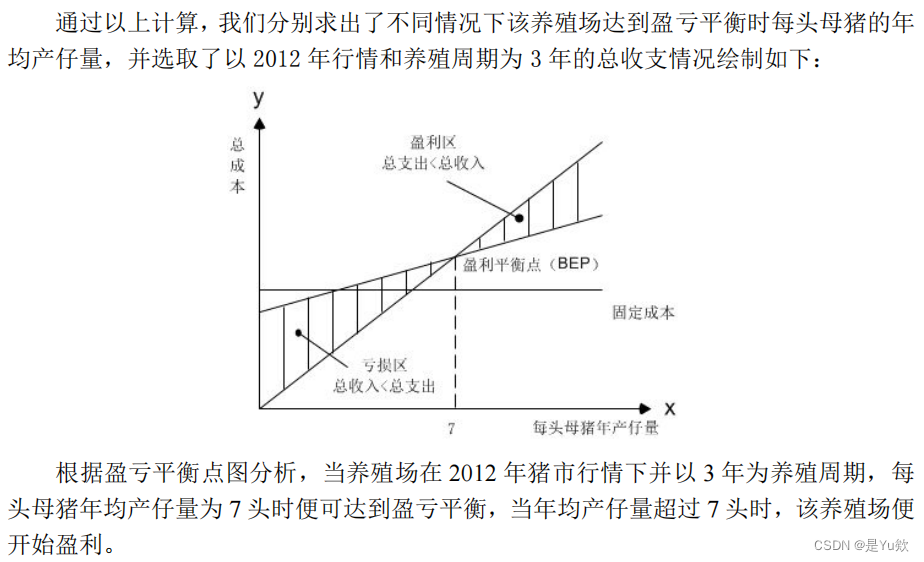
四、相关建议
通过以上对问题的求解并结合猪市行情，我们给出当前形势下生猪养殖产业的一些相关建议

问题二（求解小猪选为种猪的比例和母猪的存栏数）

母猪每年可以产两胎，每胎可以成活 9 只小猪，求使得该养殖场养殖规模达到饱和时，小猪选为种猪的比例和母猪的存栏数

一、数据准备
1.种猪淘汰率
2.公母种猪比例

二、求解比例和存栏数
1.模型准备
1）目标建立
对小猪z、母猪l和公猪w数量建立整数规划
2）条件约束
（1）养殖场最大养殖规模约束
（2）小猪数量约束约束
（3）公猪母猪比例约束
2.模型建立

3.模型求解
代码（部分修改）
小猪z、母猪y和公猪x

max=x+@floor(x*0.45)+1+y+@floor(y*0.3)+1+z;
x+@floor(x*0.45)+1+y+@floor(y*0.3)+1+z<=10000;
y*9=z+@floor(x*0.45)+1+y+@floor(y*0.3)+1;
x=(1/24)*y;
@gin(x);
@gin(y);
@gin(z);
@floor(y*0.3)+1=a;
@floor(x*0.45)+1=b;
(a+b)/((2*z+@floor(x*0.45)+1+y+@floor(y*0.3)+1))*100=p;

结果表

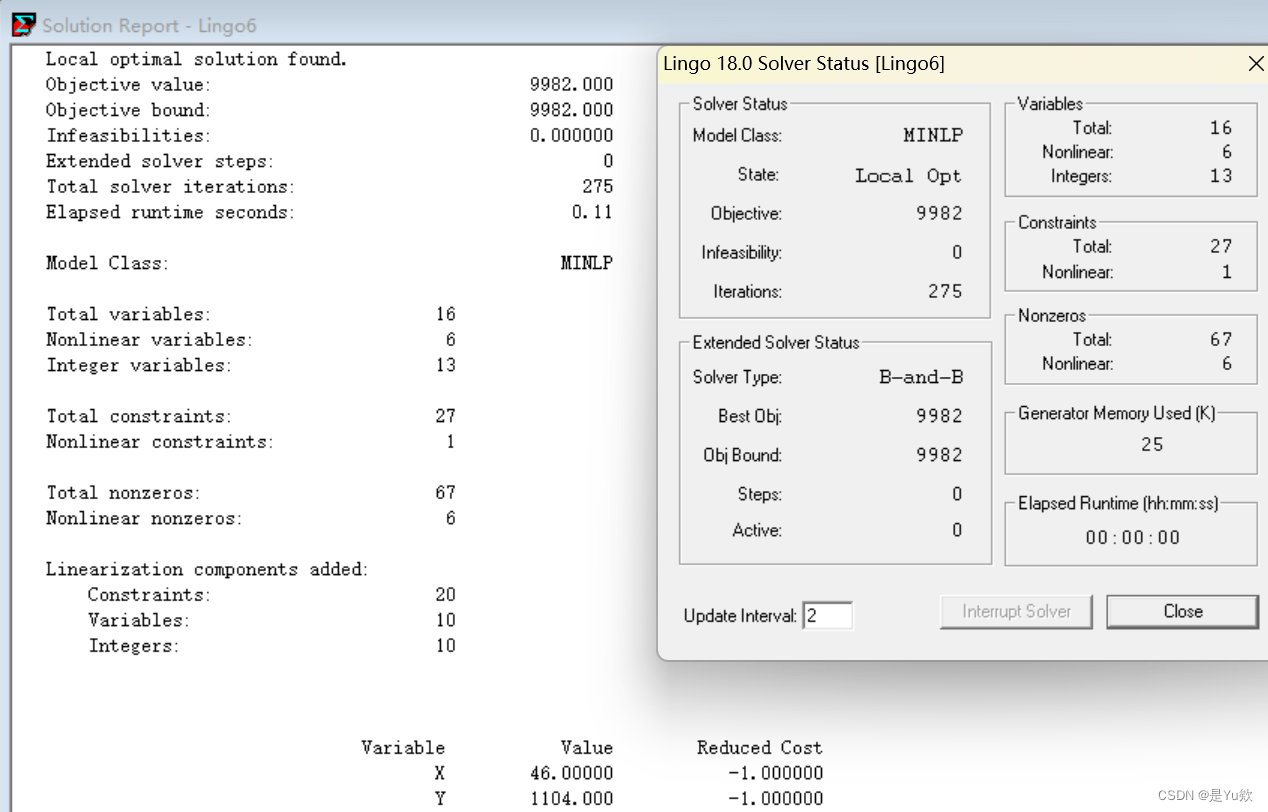
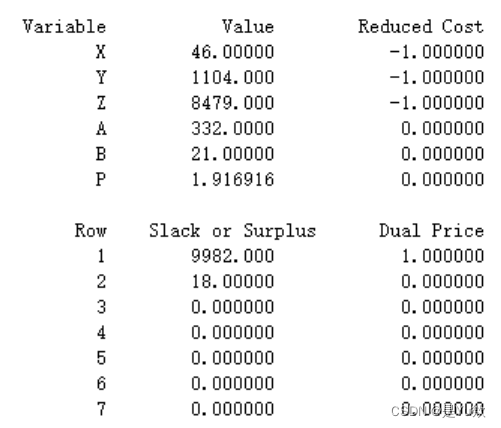
结果可能被优化过，感觉不配套。。。。

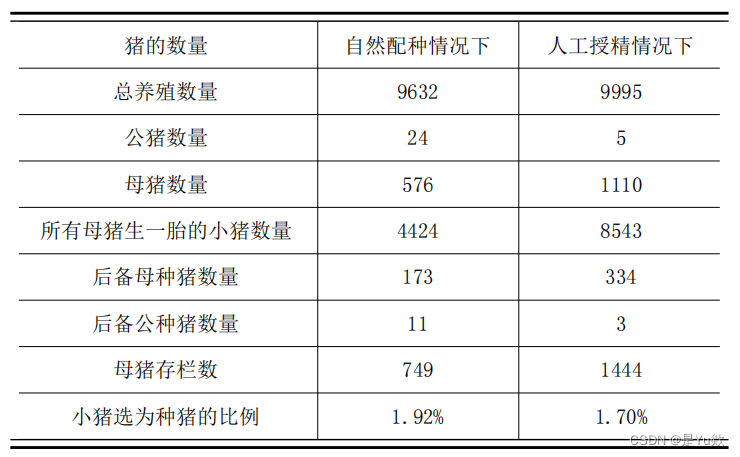
问题三（确定最佳经营策略，计算年均利润）

一、拟合饲料价格与销售价格关系
1.建立函数关系
2.利用最小二乘法拟合
（1）模型准备
①目标建立
②约束条件
（2）模型建立
（3）模型求解

二、确定未来三年饲料价格

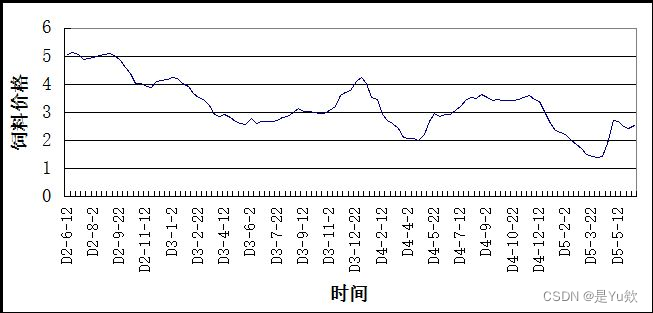
三、养殖场三年时间流程图

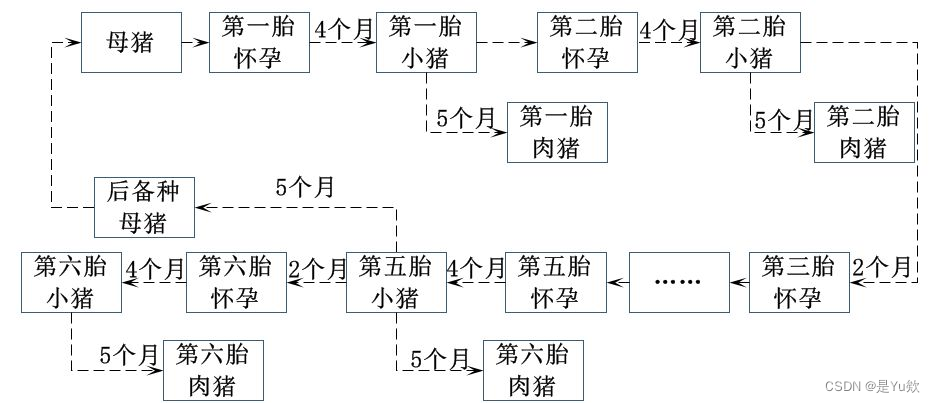
四、确定最佳经营策略和年均利润
1.数据准备
2.模型准备
1）目标建立
2）条件约束
3.模型建立

4.模型求解
代码 B Q M d
对应代码中 n q e w

第一步

sets:
bb/1..109/:a,b,c;
aa/1..6/:;
cc(aa,bb):f,p;

endsets
data:
a=@text('D:\roujia.txt');
b=@text('D:\biandongfeiyong.txt');
c=@text('D:\tianshujiange.txt');
enddata
max=n-q-e-w;
n=@sum(cc(i,j):a(j)*f(i,j)*100*8543)+8543*a(2);
q=@sum(cc(i,j):(c(j)*f(i,j)-c(j)*p(i,j)))*8543*1.5*3+8543*130*1.5*3;
e=@sum(bb(j):1452*(a(j)-7.3371)/2.3888*2.5*10);
w=@sum(cc(i,j):f(i,j)*8543*b(j))+1452*120;
@for(aa(i):@sum(bb(j):c(j)*f(i,j)-c(j)*p(i,j))>=150);
@for(aa(i)|(i#le#5):@sum(bb(j):f(i+1,j)*c(j)-f(i,j)*c(j))>=150);
!@for(aa(i)|(i#le#5):@sum(bb(j):f(i+1,j)*c(j)-f(i,j)*c(j))<=180);
@for(aa(i)|(i#le#5):@sum(bb(j):p(i+1,j)*c(j)-p(i,j)*c(j))>=180);
@for(aa(i):@sum(bb(j):f(i,j))<=1);
@for(aa(i):@sum(bb(j):p(i,j))<=1);
@for(cc(i,j):@bin(f(i,j)));
@for(cc(i,j):@bin(p(i,j)));

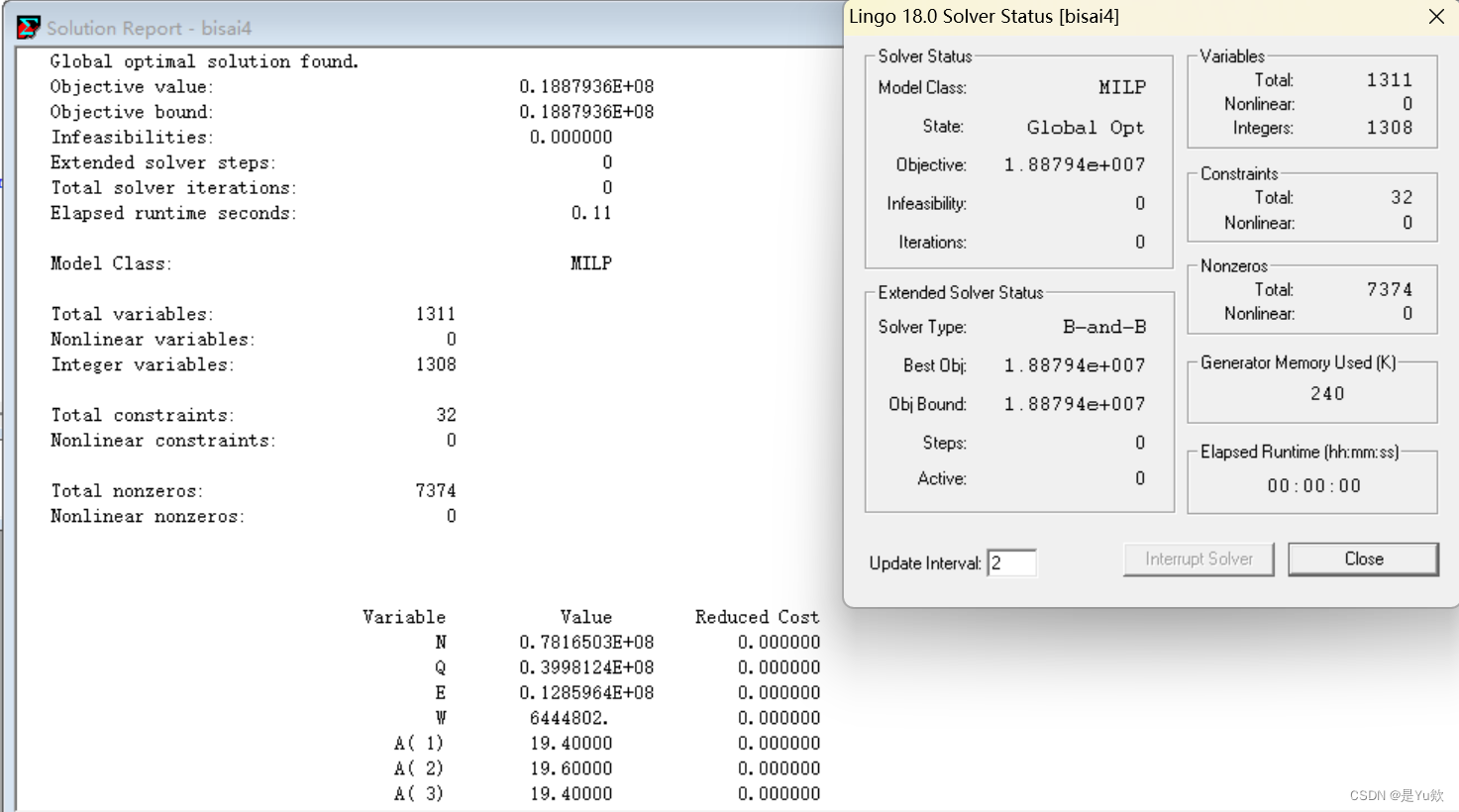
结果表

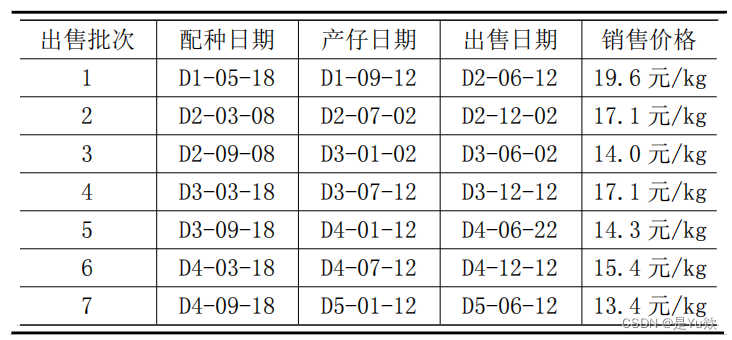
附表（部分）

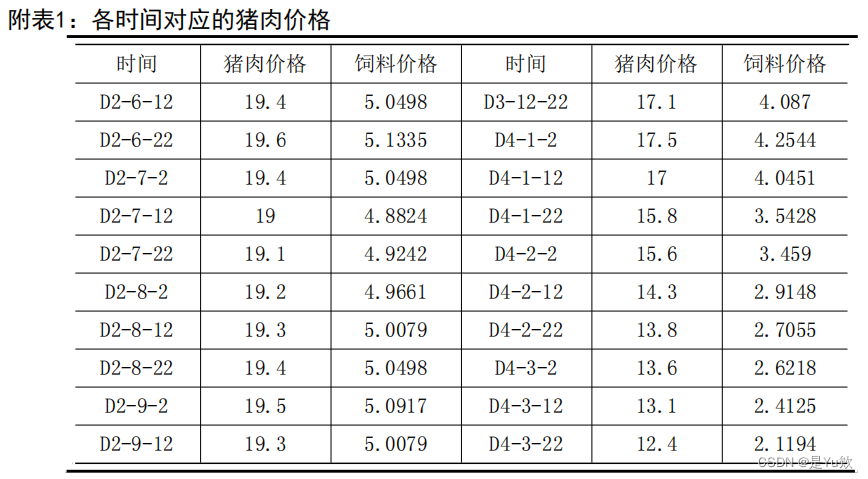
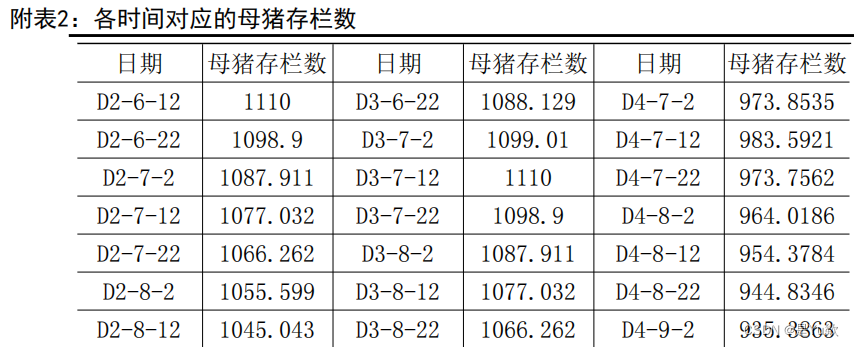
5.结果分析

问题四

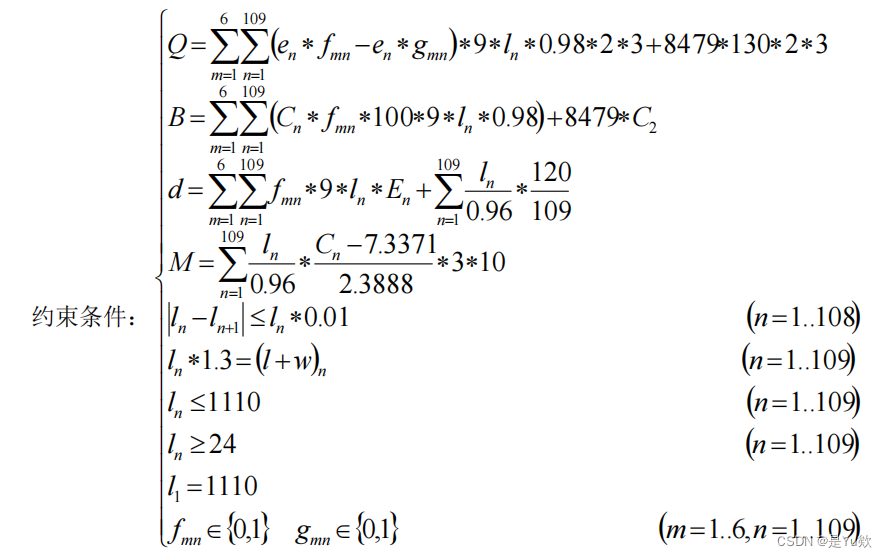
sets:
bb/1..109/:a,b,c,x,y;
aa/1..6/:;
cc(aa,bb):f,p;
endsets
data:
a=@text('D:\roujia.txt');
b=@text('D:\biandongfeiyong.txt');
c=@text('D:\tianshujiange.txt');
f=@text('D:\f.txt');
p=@text('D:\p.txt');
enddata
max=n-q-e-w;
n=@sum(cc(i,j):a(j)*f(i,j)*100*9*x(j)*0.98)+8479*a(2);
q=@sum(cc(i,j):(c(j)*f(i,j)-c(j)*p(i,j))*9*x(j)*0.98*1.5*3)+8479*130*1.5*3;
e=@sum(bb(j):x(j)/0.96*(a(j)-7.3371)/2.3888*2.5*10);
w=@sum(cc(i,j):f(i,j)*9*x(j)*0.98*b(j))+@sum(bb(j):x(j)/0.96)/109*120;
!@for(aa(i):@sum(bb(j):c(j)*f(i,j)-c(j)*p(i,j))>=150);
!@for(aa(i)|(i#le#5):@sum(bb(j):f(i+1,j)*c(j)-f(i,j)*c(j))>=150);
!@for(aa(i)|(i#le#5):@sum(bb(j):p(i+1,j)*c(j)-p(i,j)*c(j))>=180);
x(1)=1110;
@for(bb(j):x(j)<=1110);
@for(bb(j):x(j)>=24);
!@for(bb(j)|(j#le#108):@if(x(j+1)#ge#x(j),x(j+1)*0.1,x(j)*0.1)=@abs(x(j+1)-x(j)));
@for(bb(j)|(j#le#108):@abs(x(j)-x(j+1))<=x(j)*0.01);
!@for(aa(i):@sum(bb(j):f(i,j))<=1);
!@for(aa(i):@sum(bb(j):p(i,j))<=1);
@for(cc(i,j):@bin(f(i,j)));
@for(cc(i,j):@bin(p(i,j)));
@for(bb(j):x(j)*1.3=y(j));

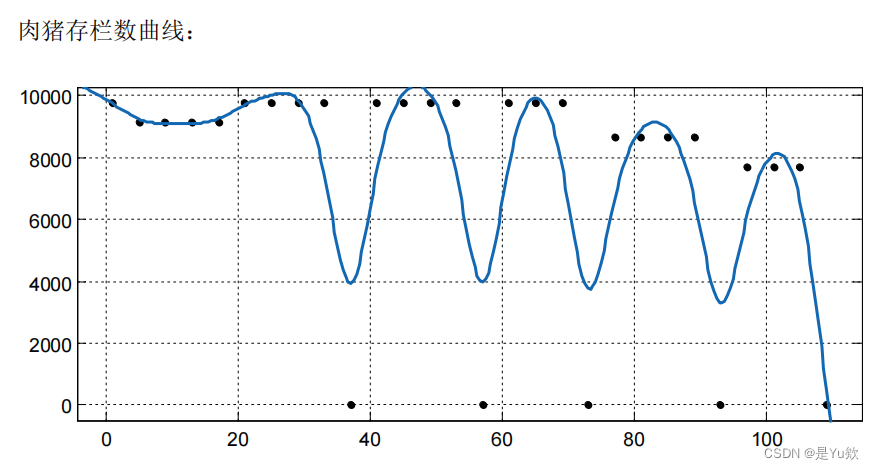
母猪数量

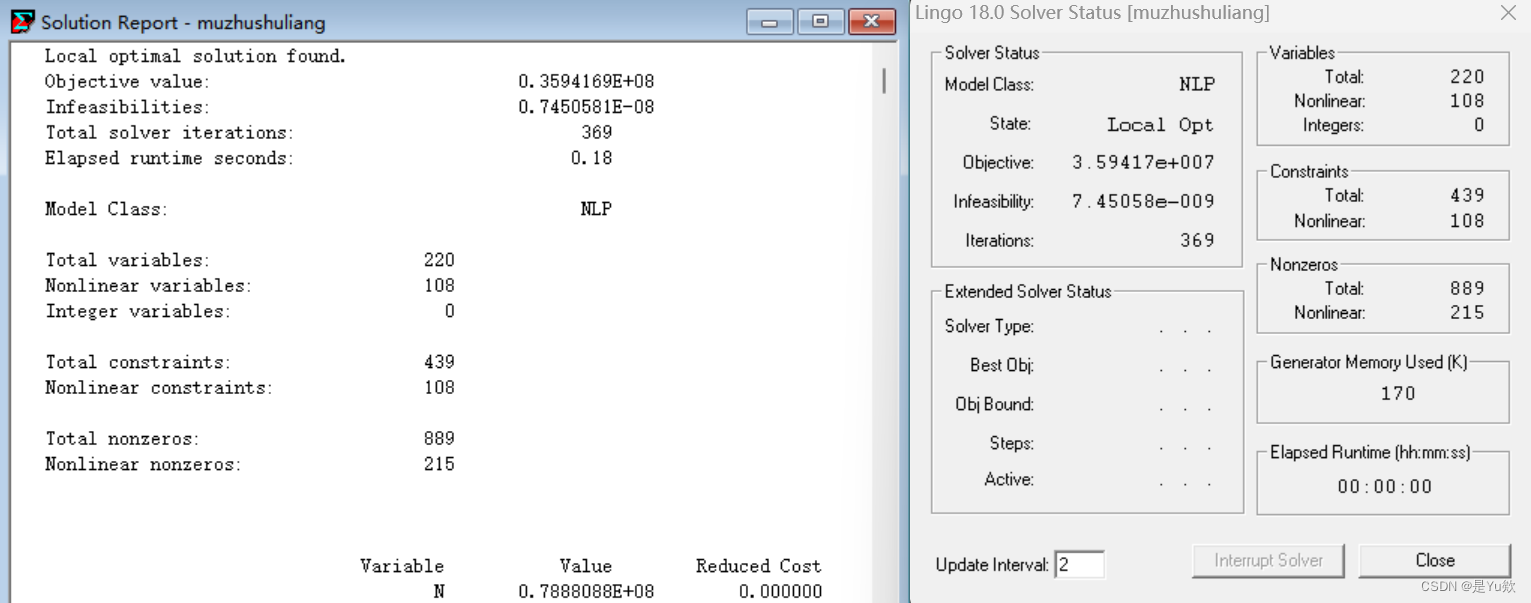
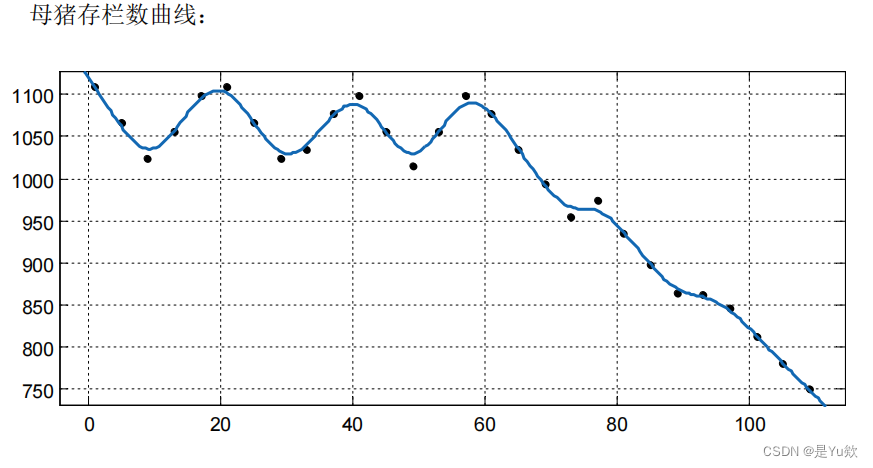
模型推广与评价

1.模型评价
好的方面：
1.对所收集来的数据进行整理，并对其进行筛选，将合理数据用于计算中；
2.利用拟合最小二乘法来分析预测数据，更加具有说服力和理论性；
3.结合不同种实际情况，使所建立的模型更加科学、合理。
有待改进的地方：
1.本模型所收集的数据有限，计算精度不高，得到的结果可能同实际情况有所出入。

2.模型推广
所建立的模型考虑到的因素比较全面，并详细的给出了经营策略，可以应用到实际规划中。
根据文中所建立的模型，依据近几年市场价格涨跌趋势，预测未来几年市场营销情况，即可以提前做出预判。