利用二阶权重统计增强对抗训练

对抗训练已被证明是提高深度神经网络鲁棒性的最有效方法之一。它被形式化为对模型权重和对抗性扰动的最小-最大优化，其中权重可以通过梯度下降方法（如SGD）进行优化。在本文中，我们证明了将模型权重视为随机变量允许通过关于权重的二阶统计优化（S2O）来增强对抗性训练。通过放宽先前PAC贝叶斯框架中所有权重都是统计独立的常见（但不现实）假设，我们导出了一个改进的PAC贝叶斯对抗性泛化界，这表明优化权重的二阶统计可以有效地收紧该界。除了这一理论见解之外，我们还进行了一系列广泛的实验，这些实验表明，S2O不仅在单独使用时提高了训练神经网络的鲁棒性和通用性，而且还很容易地集成到最先进的对抗性训练技术中，如TRADES、AWP、MART和AVMixup，从而对这些技术进行了可衡量的改进。

本文认为，对抗训练可以从考虑权重的二阶统计中受益。我们的理论论证是通过更新PAC贝叶斯框架获得的，该框架以原始格式处理模型泛化，通过考虑对抗鲁棒性和二阶统计加权。在贝叶斯机制下，权重是随机变量，我们从两个方面对框架进行更新，首先，通过放宽所有权重在统计上独立的不合理假设，我们引入了权重的二阶统计量，即权重相关矩阵，其次除了模型泛化之外，本文还考虑了对抗鲁棒性。

该更新的框架表明，我们可以通过监控权重相关矩阵的一些范数来控制训练期间的对抗性泛化边界。为了实现这种控制，我们需要分别估计权重相关矩阵和进行训练的方法。对前者采用了两种采样方法和拉普拉斯近似算法，对于后者也就是训练采用新的二阶统计优化算法。

S2o不仅可以显著提高训练模型的鲁棒性和泛化能力，而且可以进一步增强现有的对抗性训练技术。而且s20的增强仅导致训练时间的边际增加。

符号说明

我们认为是每层具有h个隐藏单元和激活函数的n层神经网络，

在第l层，激活函数之前和之后的潜在表示为：

 对抗性泛化界限

设是从训练数据中学习并由W参数化的任何预测器。我们考虑在学习权重W上以的形式的分布Q，并用（U的矢量化）表示其分布也可能取决于训练数据的多变量随机变量。

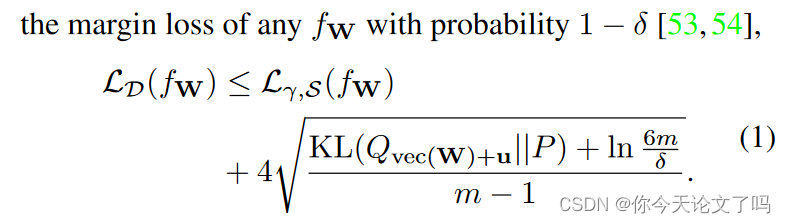
 留个坑，这个文章公式太多，没有完全搞懂，