线性表
线性表括顺序表和链式表。
栈(Stack)是只允许在一端进行插入或删除操作的线性表。应用:表达式求值,函数递归调用
队列(Queue)是只允许在一端进行插入,在另一端删除的线性表。应用:树和图的广度优先遍历,操作系统FCFS算法
双端队列:只允许从两端插入、两端删除的线性表
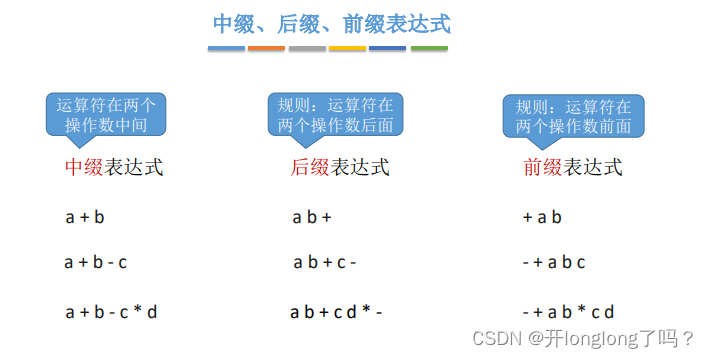
前缀、后缀、中缀表达式

串
KMP算法
假设匹配字符串为s,模板字符串为t,算法核心是计算出一个next数组,next[j]的含义是当模板字符串的t[j]不匹配时,往后挪移到next[j]下标的位置。
树
树是由零个或多个结点组成的具有层级关系的数据结构。
树是n(n≥0)个结点的有限集合,n = 0时,称为空树,这是一种特殊情况。在任意一棵非空树中应满足:
1)有且仅有一个特定的称为根的结点。
2)当n > 1时,其余结点可分为m(m > 0)个互不相交的有限集合T1, T2,…, Tm,其中每个集合本身又是一棵树,并且称为根结点的子树。
属性:
- 结点的层次(深度)―—从上往下数
- 结点的高度――从下往上数
- 树的高度(深度)――总共多少层
- 结点的度――有几个孩子(分支),树的结点数 = 各结点度数之和 + 1
- 树的度――各结点的度的最大值
有序树——逻辑上看,树中结点的各子树从左至右是有次序的,不能互换。反之就是无序树
森林。森林是m(m≥0)棵互不相交的树的集合
二叉树
二叉树是有序树
特殊二叉树:
- 满二叉树,每层都是满的
- 完全二叉树,除了最后一层可以不满
- 二叉排序树(二叉查找树、二叉搜索树):对于每个结点,左子树所有结点值 < 父节点值 < 右子树所有节点值,不允许结点之间有重复值。
- 平衡二叉树。树上任一结点的左子树和右子树的深度之差不超过1
二叉树遍历:先序Preorder——根、左、右;中序Inorder——左、根、右;后序Postorder——左、右、根;bfs层序遍历
线索二叉树是对二叉树进行线索化,使某些二叉树节点可以直接访问到左右子节点以外的节点。
对于二叉树进行先序遍历得到一个先序序列,先序线索化结点的左孩子指向序列中的前驱节点,右孩子指向后继节点。
同样的,依据中序序列、后序序列可以得到中序、后序的线索二叉树。
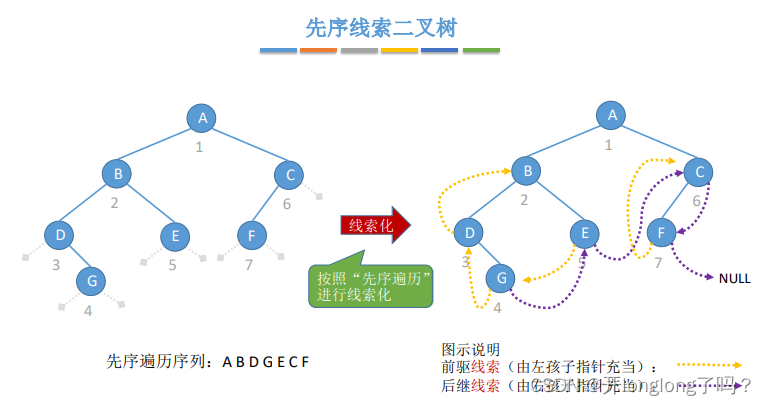
树和二叉树之间的转换,左孩子右兄弟
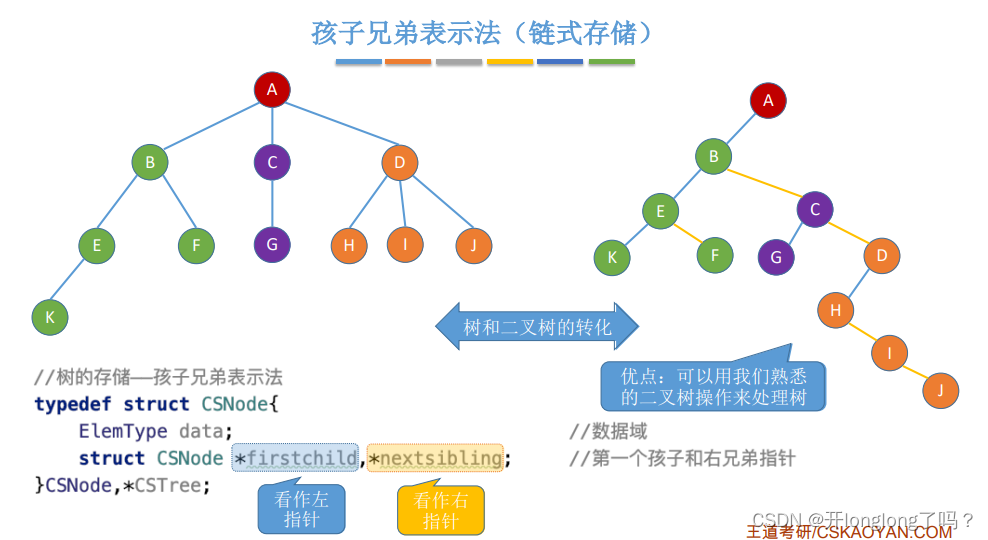
森林和二叉树的转换依然是左孩子右兄弟,森林中各个树的根结点视为兄弟关系
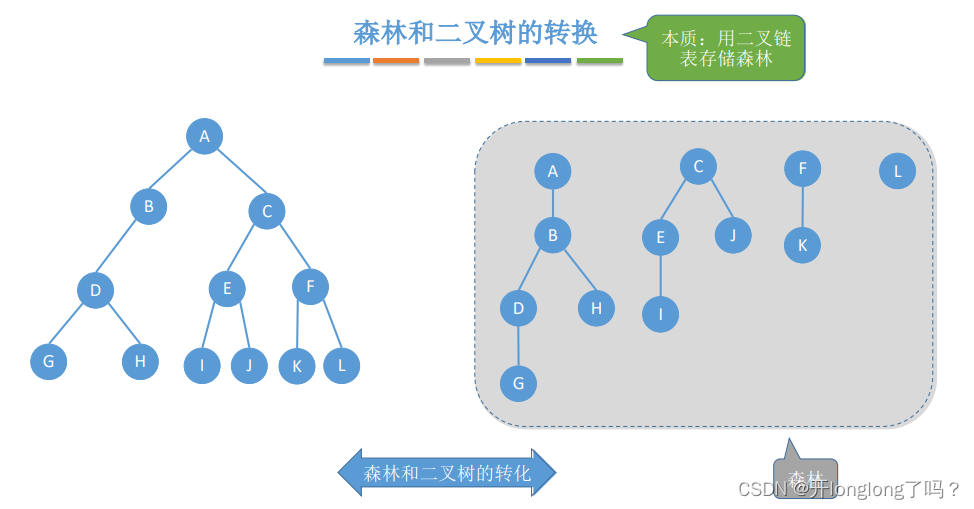
二叉排序树
二叉排序树的插入:若原二叉排序树为空,则直接插入结点;否则,若关键字k小于根结点值,则递归插入到左子树(如果左子树为空则直接挂在左孩子结点上),若关键字k大于根结点值,则递归插入到右子树(同上)。
对于二叉排序树来说,它的中序遍历序列是一个递增序列。
二叉排序树的删除:
① 若被删除结点z是叶结点,则直接删除,不会破坏二叉排序树的性质。
② 若结点z只有一棵左子树或右子树,则让z的子树成为z父结点的子树,替代z的位置。
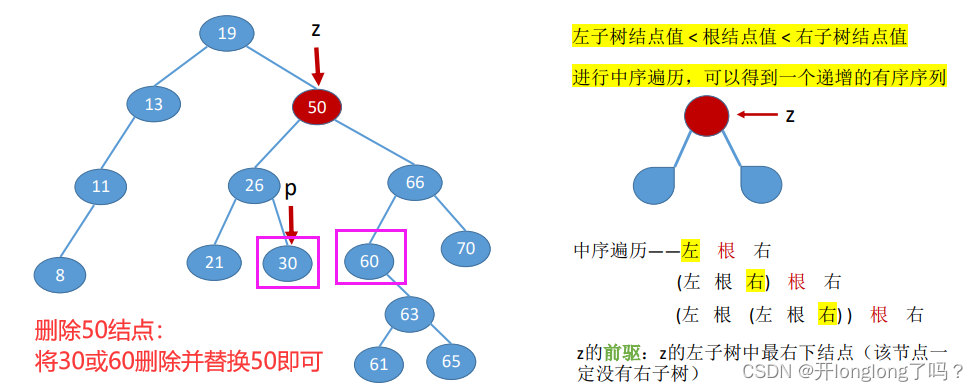
③ 若结点z有左、右两棵子树,我们删除左子树中值最大的结点或者右子树中值最小的结点,然后用该节点替换结点z即可。
在这里要解释一下,由于中序遍历是递增的,所以左子树值最大的结点就是中序序列中z结点的前驱节点,右子树中值最小的结点就是z节点的后继节点。
对于左子树值最大的节点,因为它的值在子树中是最大的,所以必然不含右孩子,所以肯定符合情况①或情况②,很容易删除;对于右子树中值最小的结点也是同样的道理。
其实还有一种寻找左子树中值最大的结点的方法,从左子节点开始,递归搜索它的右孩子,右孩子为空时,该节点就是左子树中值最大的结点。
平衡二叉树
平衡二叉树,也就是每个结点的左右子树高度不超过1,关键问题在于插入新结点时如何维护二叉树的平衡性。
在插入结点时,每次调整的对象都是“最小不平衡子树”
结点的平衡因子=左子树高-右子树高。
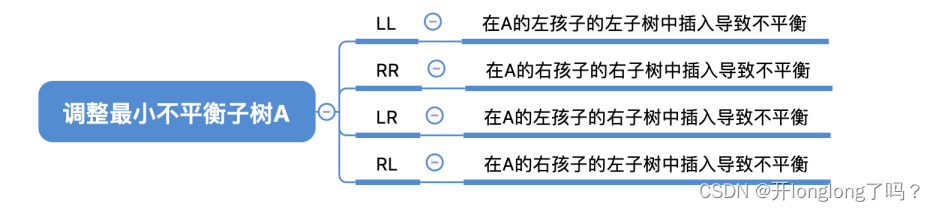
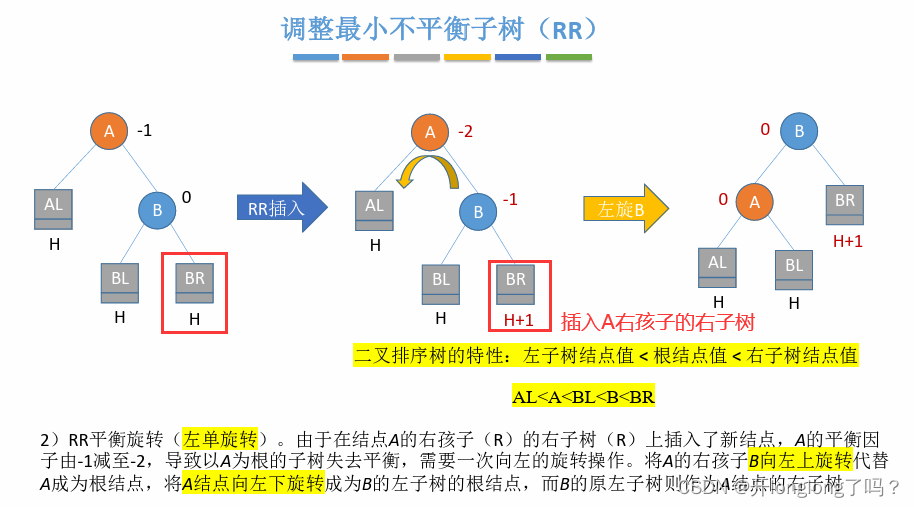
LL和RR很像,是对称的关系

LR和RL待补充。。。。
哈夫曼树
结点的权:有某种现实含义的数值(如:表示结点的重要性等)
结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积
树的带权路径长度:树中所有叶结点的带权路径长度之和(WPL,Weighted Path Length)
在含有n个带权叶结点的二叉树中,其中**带权路径长度(WPL)**最小的二叉树称为哈夫曼树,也称最优二叉树
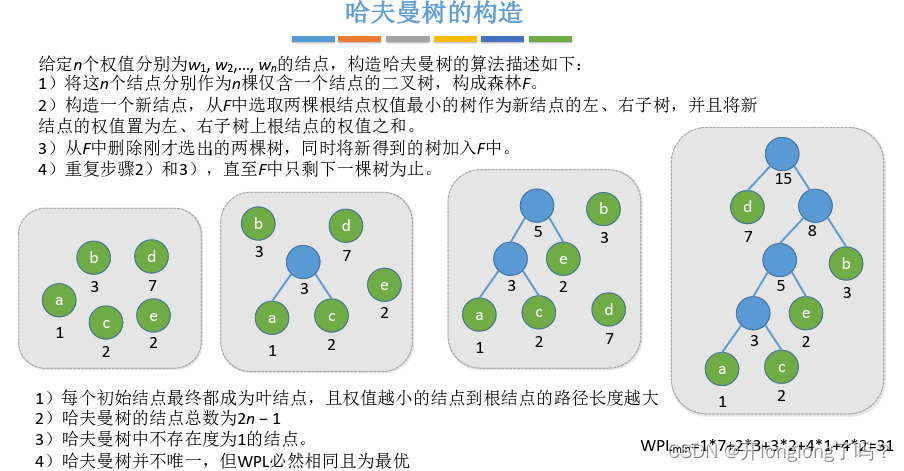
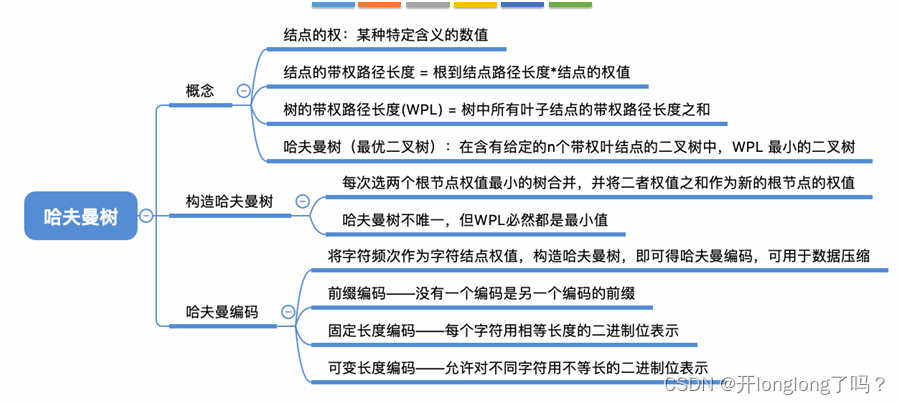
图
对于无向图:顶点v的度是指依附于该顶点的边的条数,记为TD(v)。
对于有向图:
入度是以顶点v为终点的有向边的数目,记为ID(v);
出度是以顶点v为起点的有向边的数目,记为OD(v)。
顶点v的度等于其入度和出度之和,即TD(v) = ID(v) + OD(v)。

连通的概念存在于无向图中,强连通的概念存在于有向图中
若图G中任意两个顶点都是连通的,则称图G为连通图,否则称为非连通图。
若图中任何一对顶点都是强连通的,则称此图为强连通图。
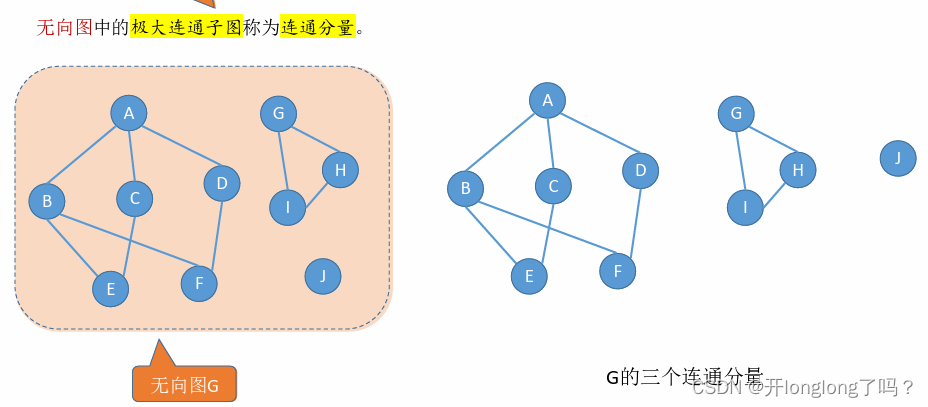
无向图中的极大连通子图称为连通分量。
有向图中的极大强连通子图称为有向图的强连通分量。
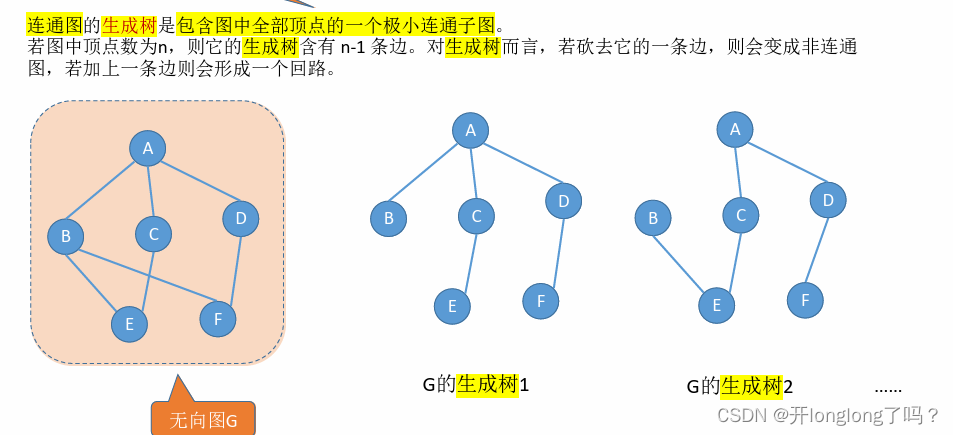
连通图的生成树是包含图中全部顶点的一个极小连通子图。
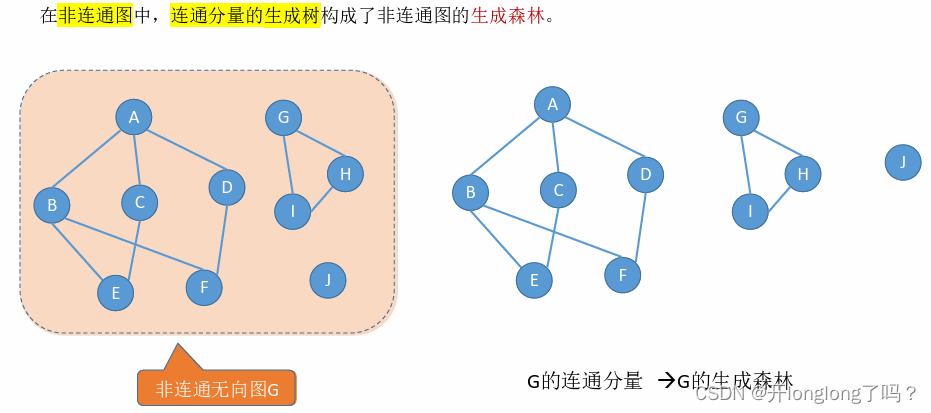
在非连通图中,连通分量的生成树构成了非连通图的生成森林。

无向完全图——无向图中任意两个顶点之间都存在边
有向完全图——有向图中任意两个顶点都存在都存在方向相反的两条弧
特殊的图:
树——不存在回路,且连通的无向图
有向树——一个顶点的入度为0、其余顶点的入度均为1的有向图,称为有向树。

邻接矩阵存图,空间复杂度O(V ^ 2), V是顶点数
邻接表存图,空间复杂度O(V + E),E是边数
十字链表存有向图、邻接多重表存无向图待补充。。。
图的遍历
BFS广度优先遍历对应广度优先生成树
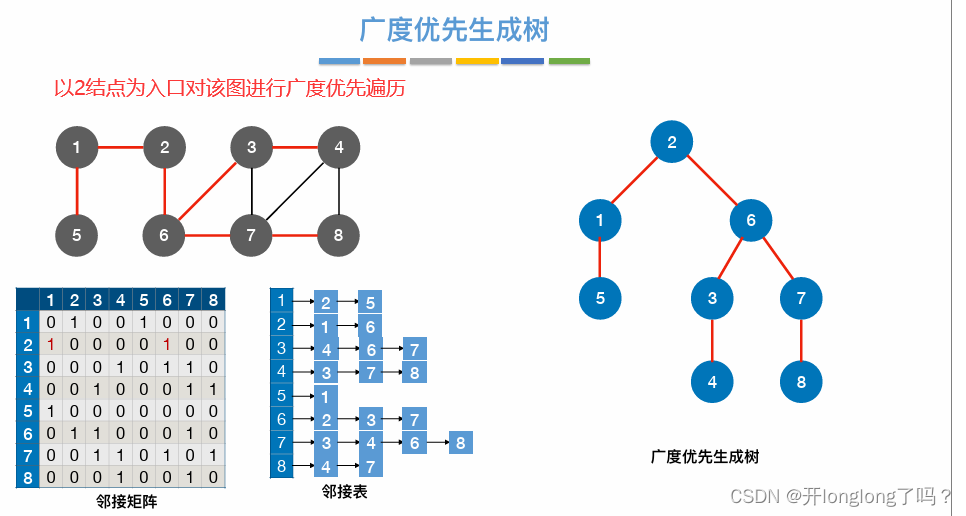
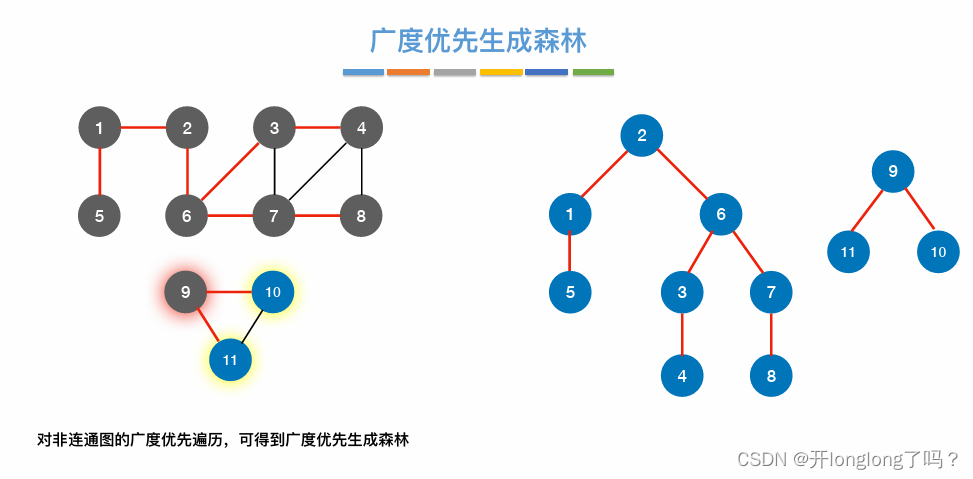
BFS,对应深度优先生成树
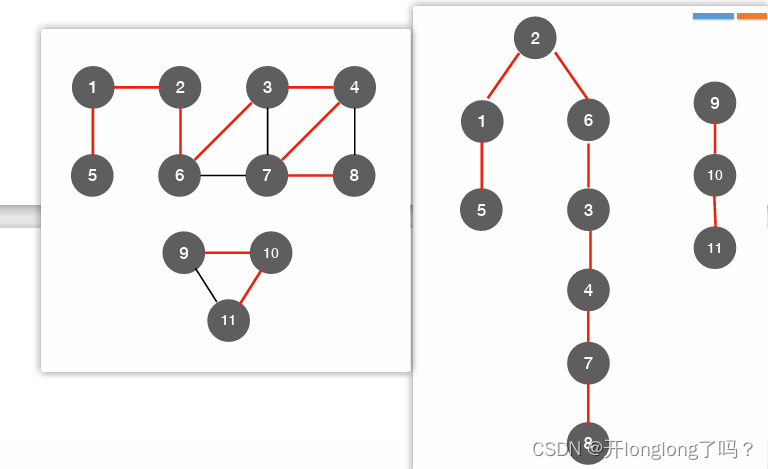
最小生成树
很简单,不说了。

最短路
bfs可以求无权最短路。
dijkstra求单源最短路,要求边权为非负数,复杂度O(V ^ 2)
floyd求多源最短路,边权可以为负数
拓扑排序,逆拓扑排序
EOV图的关键路径,求关键路径步骤如下:
- 起始事件的最早开始时间是0,顺着箭头的方向正向推导,求得各个事件的最早开始时间。代码上体现为BFS。
- 在上个步骤中已求得结束事件的最早开始时间,结束事件的最晚开始时间等于最早开始时间,然后逆着箭头的方向倒着推导,求出各个时间的最晚开始时间。代码上体现为BFS。
- 最早开始时间等于最晚开始时间的事件组成的路径,就是关键路径。
活动的最早开始事件等于前驱事件的最早开始事件,活动的最晚开始时间等于后继事件的最晚开始时间 - 活动持续时间

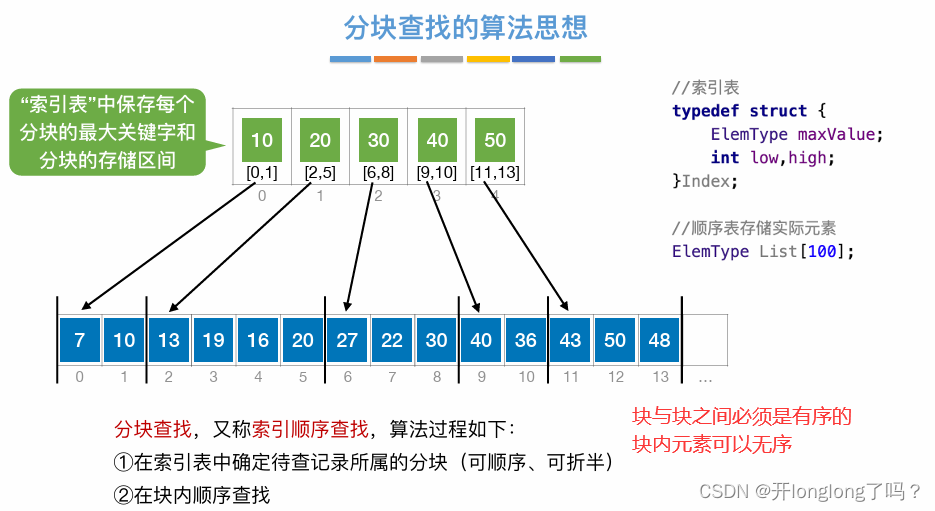
查找
折半查找时间复杂度= O(log2n)
顺序查找的时间复杂度= O(n)
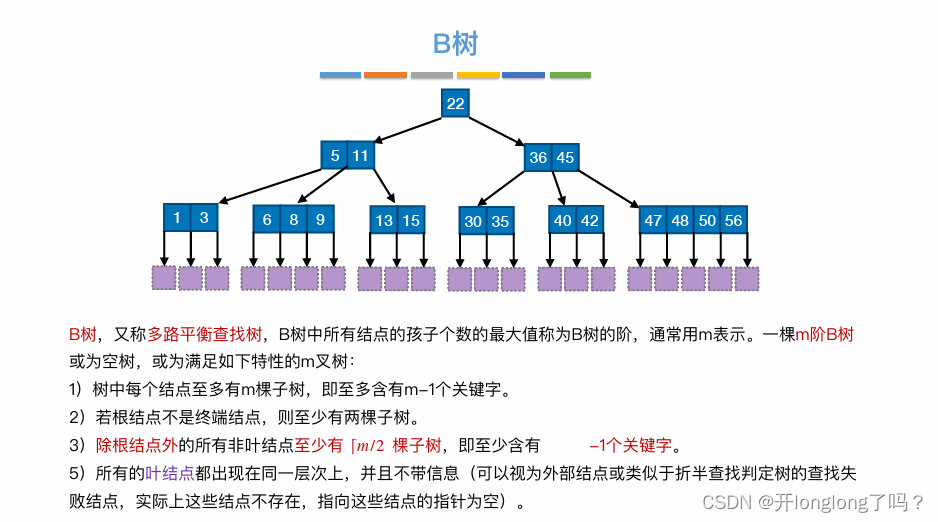
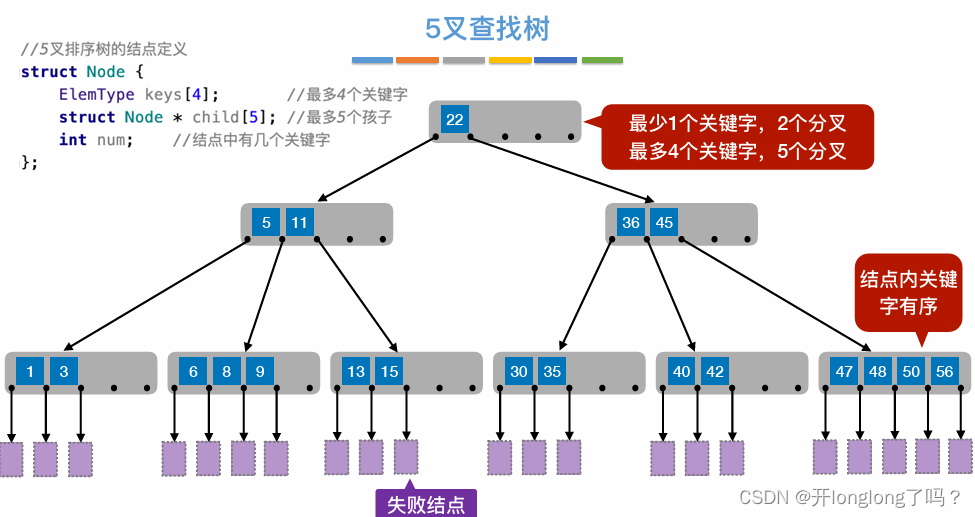
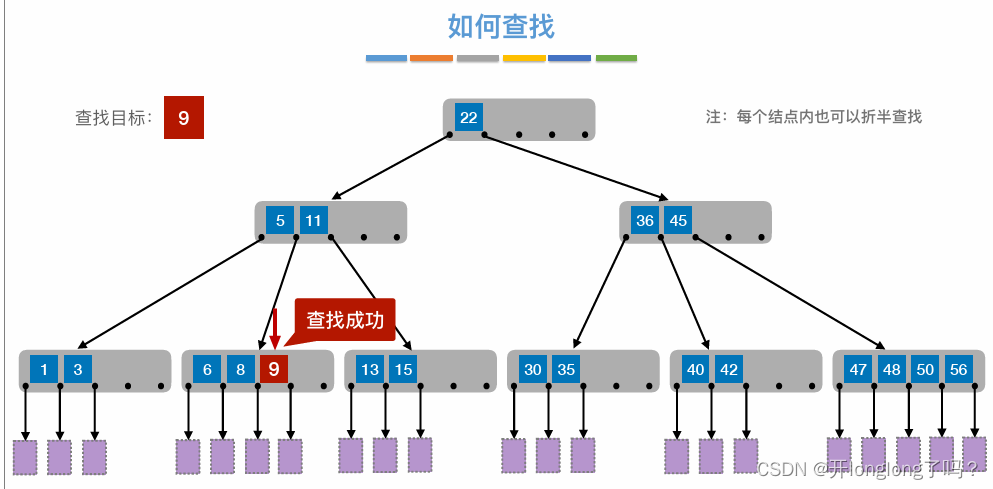
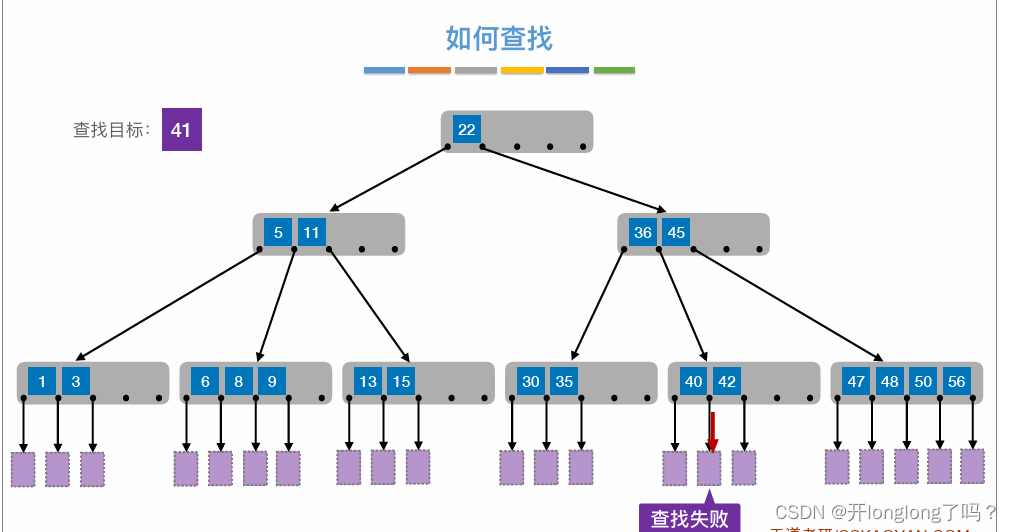
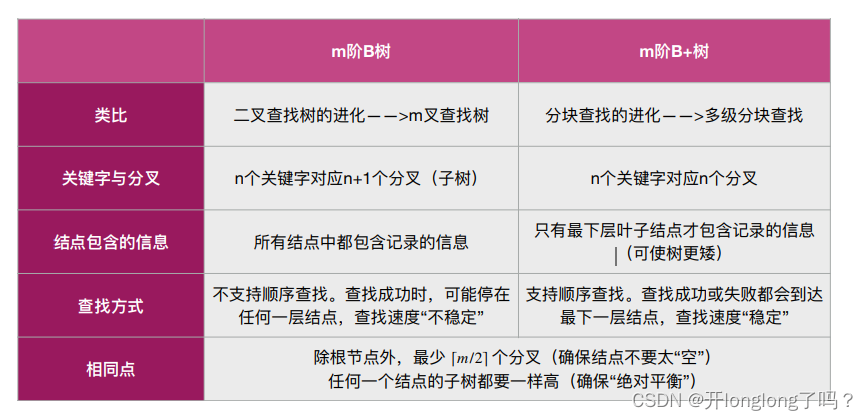
B树
B树是二叉排序树的plus版,一个结点内可以多个值,一个结点可以有多个子结点。结点内的值是有序的,多个子结点的值之间也是有序的。
m阶B树每个结点至多含有m-1个关键字
B树的插入与删除
这篇文章写的比较好
B树的插入操作,一定是插入到树的叶子结点里,从树根开始递归搜索,找到应该插入的那个叶子结点然后插入即可。
如果插入后叶子结点的值个数等于树的阶,那么需要把这个结点以中间值为界限分裂成两个结点,把中间值送给父节点。如果父节点的值的个数也等于树的阶,那么对父节点递归进行分裂操作。
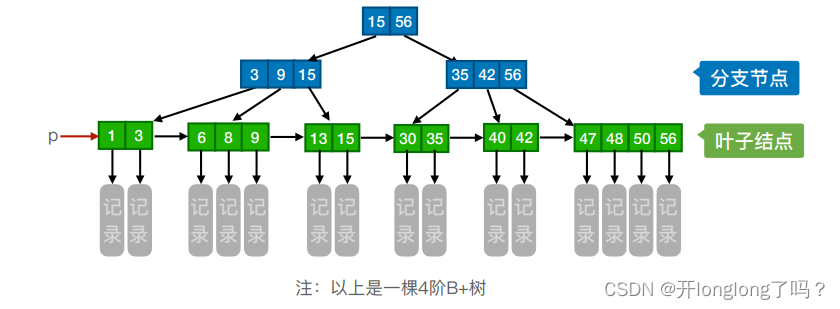
B+树
在B树中,叶子结点和非叶子结点都可以存放值,然而B+树的非叶子节点是不保存数据的,只起到索引作用,它的叶子节点才保存数据。
B+ 树 的数据结构中,叶子节点之间形成了单向链表。每一个节点的指针,通过叶子节点指向下一个元素。
典型应⽤:关系型数据库的“索引”(如MySQL)
在B+树中,⾮叶结点不含有该关键字对应记录的存储地址。 可以使⼀个磁盘块可以包含更多个关键字,使得B+树的阶更⼤,树⾼更矮,读磁盘次数更少,查找更快
红黑树
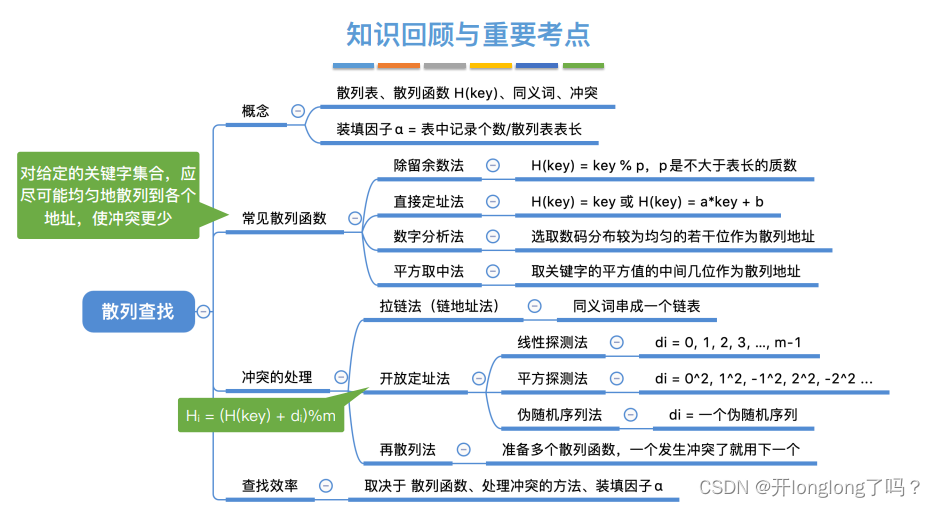
散列查找 hash查找
散列表(Hash Table),⼜称哈希表。是⼀种数据结构,特点是:数据元素的关键字与其存储地址直接相关
把key值映射到hash表的过程称为散列函数,常⻅的散列函数:除留余数法 —— H(key) = key % p
当有两个key映射到相同的hash值时,我们称之为哈希冲突,可以使用“拉链法”解决这种冲突,也就是邻接表,如下图所示,
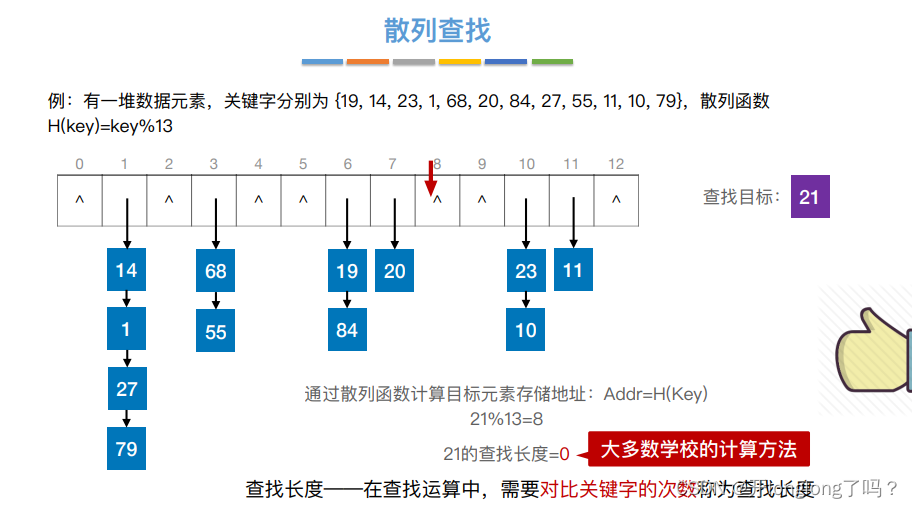
也可以用开放定址法解决冲突,当插入元素存在hash冲突时把它存放在邻近的空位置里,如下图中的1、68、27,他们的hash值本来都是1,但因为冲突所以变成了2 3 4。
如何确定具体存放在哪个相邻位置里,与查找哈希表时的探测方法有关:
①线性探测法—— di = 0, 1, 2, 3, …, m-1;即发⽣冲突时,每次往后探测相邻的下⼀个单元是否为空。我们把冲突的元素存储在高于当前hash地址且最邻近的空位置里,如下图中的1、68、27,他们的hash值本来都是1,但因为冲突所以变成了2 3 4。
②平⽅探测法。当di = 02, 12, -12, 22, -22, …, k2, -k2时,称为平⽅探测法,⼜称⼆次探测法其中k≤m/2。我们把冲突的元素存储当前hash地址加减k ^ 2的位置。
③伪随机序列法。di 是⼀个伪随机序列,如 di= 0, 5, 24, 11, …

排序

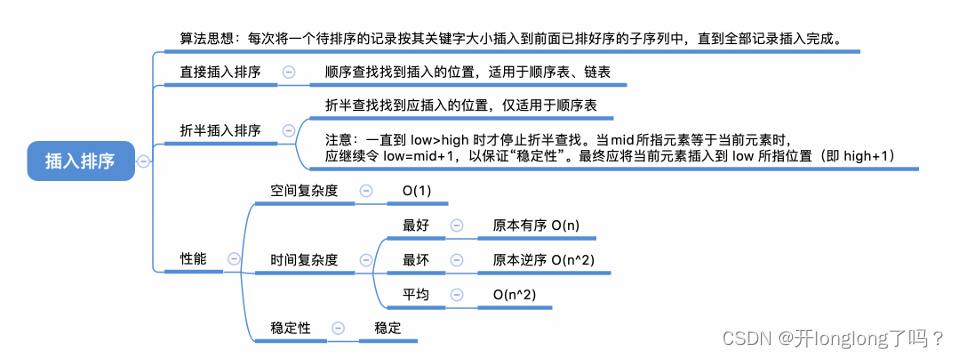
插入排序
将元素插入有序区间时,可使用二分查找来优化。

希尔排序
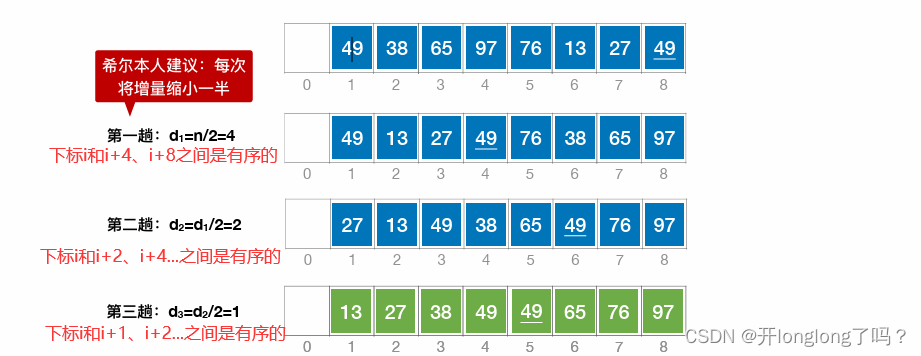
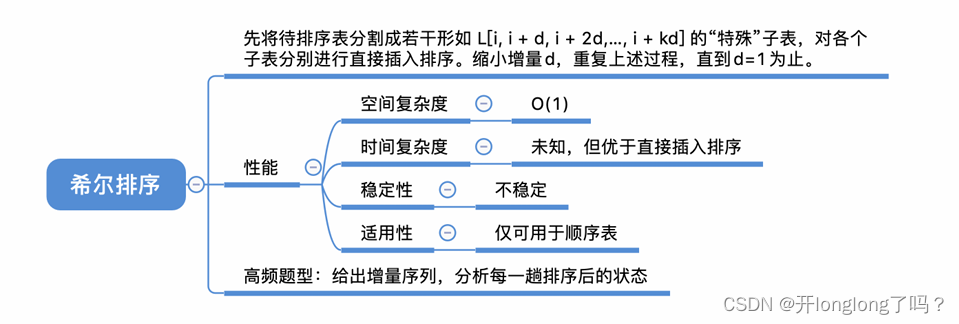
希尔排序:先将待排序表分割成若⼲形如 L[i, i + d, i + 2d,…, i + kd] 的“特殊”⼦表,对各个⼦表分别进⾏直接插⼊排序。缩⼩增量d,重复上述过程,直到d=1为⽌。
初始增量选择n/2,每次迭代增量减半
冒泡排序
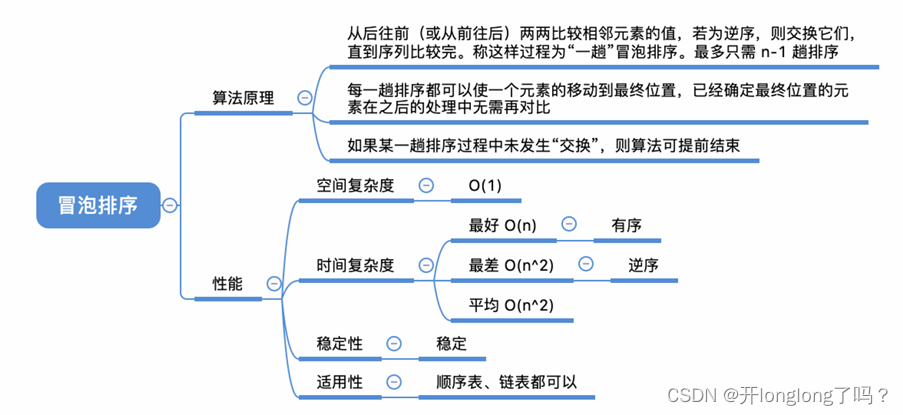
按照某种大小规则连续交换相邻两个元素的位置,使最大或最小的元素冒泡到序列首部或尾部,然后对剩余序列重复冒泡操作。
快速排序
在一段序列中随便选一个数,不妨计这个数为v,然后对序列元素进行一系列交换操作,使v左边的元素均小于v,v右边的元素均大于v。这样就把序列分成了三段,左边的都小于v,中间的都等于v,右边的都大于v,对左右子序列递归上述操作,即可完成排序。

排序不稳定。不适用链表。
时间复杂度=O(n*递归层数)
最好时间复杂度=O(nlog2n)
最坏时间复杂度=O(n2)
平均时间复杂度=O(nlog2n)
空间复杂度=O(递归层数)
最好空间复杂度=O(log2n)
最坏空间复杂度=O(n)
若序列原本就有序或逆序,则时、空复杂度最⾼(可优化,尽量选择可以把数据中分的枢轴元素。)
选择排序
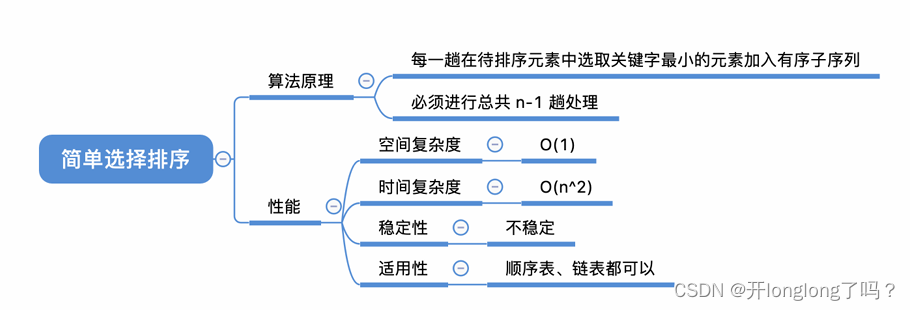
遍历一个序列,选出最小的数把它挪动到序列头部。然后对除首部以外的剩余序列迭代上述操作,即可完成排序。
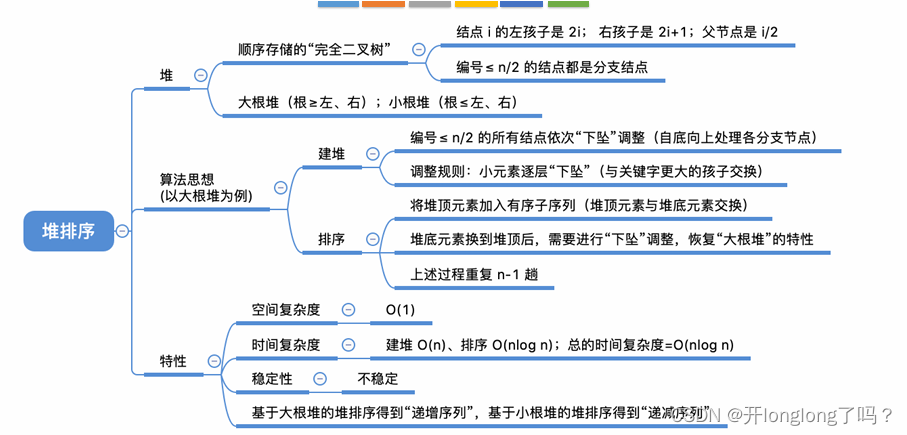
堆排序
堆是一种完全二叉树,对于每一个子树来说,都满足这样一个性质:子树的根节点的值是该子树所有结点的最大值或最小值。
用顺序表存堆比较方便。
堆的插入和删除就是简单的pushup和pushdown操作,建立堆可以看作是把一系列元素插入一个空堆。
借助堆的特性实现排序,称作堆排序。
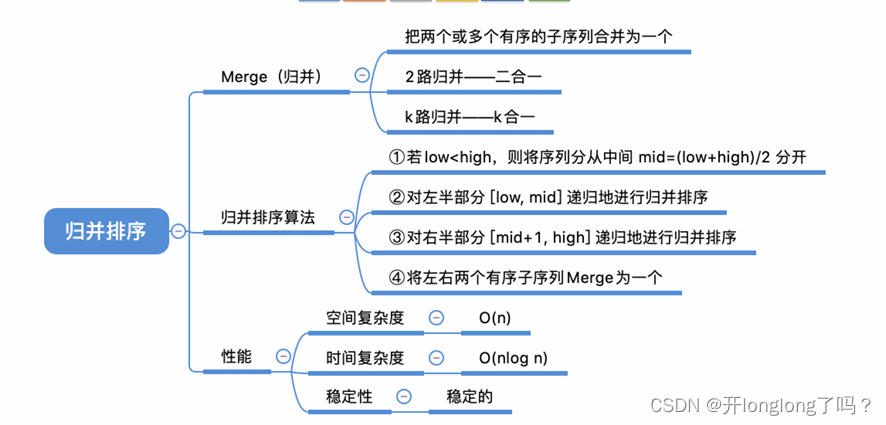
归并排序
归并排序的内容:对于一个序列,把它分成左右两部分,然后对左右子序列分别递归调用归并排序,然后把左右两个有序的子序列合并为一个有序的序列。
基数排序
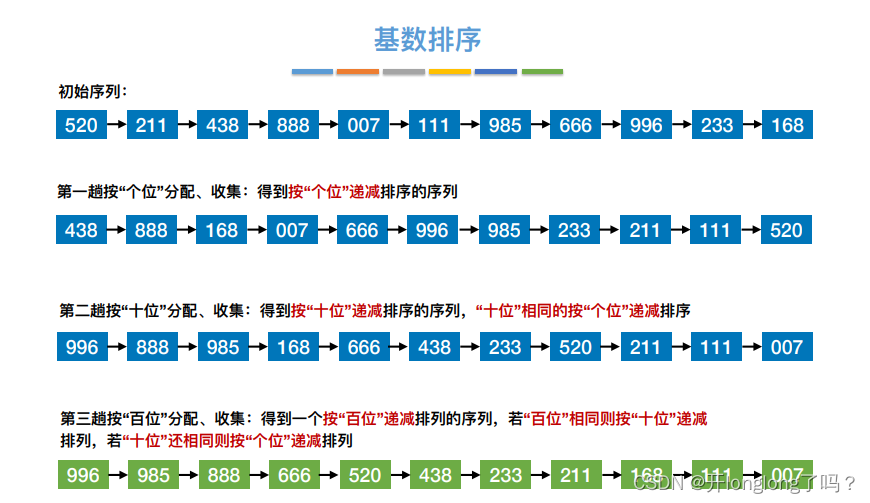
假设关键字可以拆成d个部分,每个部分可能取得r个值,总共有n个元素,那么:
- 需要 r 个辅助队列,空间复杂度 = O®
- ⼀趟分配O(n),⼀趟收集O®,总共 d 趟分配、收集,总的时间复杂度=O(d(n+r))

外部排序
指要排序的数据存储在外存中,也就是磁盘中。
磁盘的读/写以“块”为单位数据读⼊内存后才能被修改修改完了还要写回磁盘