戳气球00

news2025/1/22 16:02:17

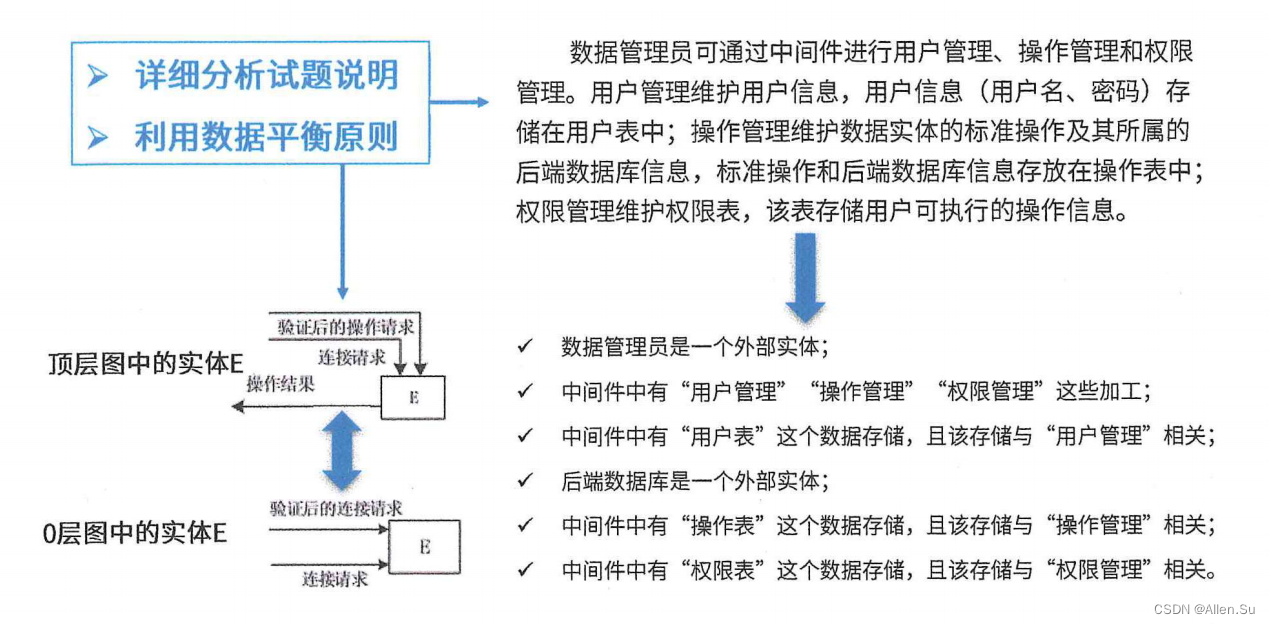
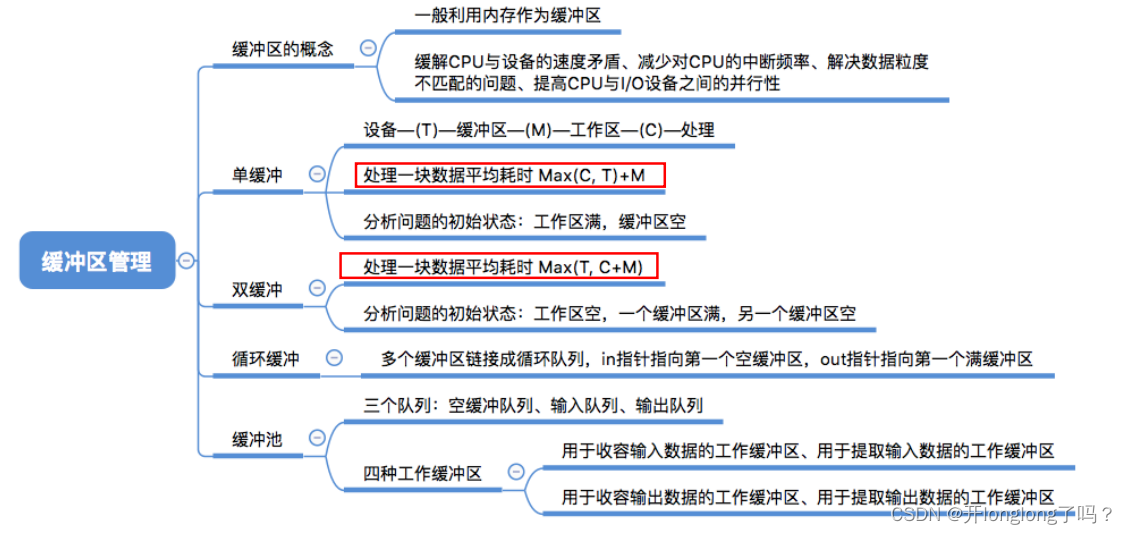
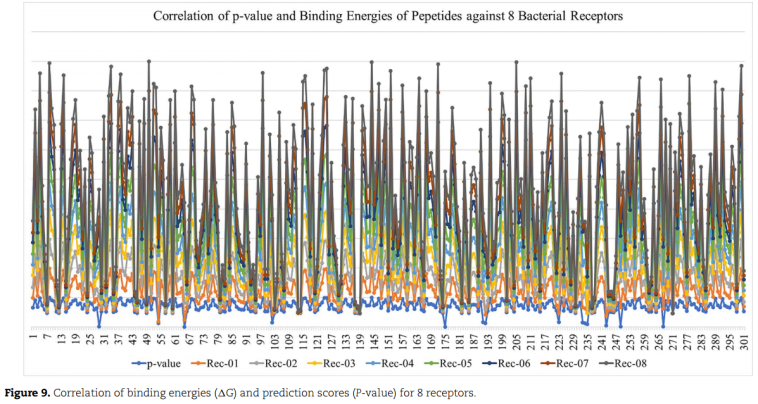
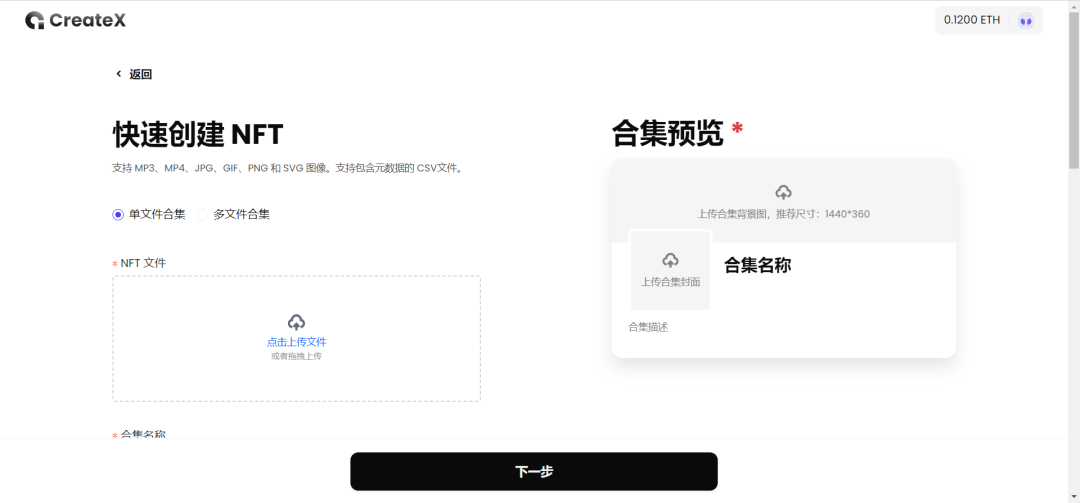
题目链接

戳气球

题目描述

注意点

求戳破所有的气球所能获得硬币的最大数量
0 <= nums[i] <= 100
1 <= n <= 300

解答思路

初始只想到深度优先遍历暴力搜索所有情况找到获得硬币的最大数量，但是时间复杂度很高一定会超时
参照题解使用动态规划解决本题，作者题解链接。其思路为：对于任意一个区间，先暂时只思考最后一个被戳爆的气球，如下图所示：

最后戳爆气球 k，那么得到的金币数量就是：total = dp[i][k] + val[i] × val[k] × val[j] + dp[k][j]，为什么前后只要加上 dp[i][k] 和 dp[k][j] 的值就是最大金币数，因为 k 是最后一个被戳爆的，所以 (i, j) 区间中 k 两边的东西必然是先各自被戳爆了的，左右两边互不干扰
所以动态规划的思路是，从小到大从左到右取所有开区间（区间范围i ~ j最小为3），求每个区间最后戳爆区间内中间任意一个气球k的所有情况，求出获得金币数最大值，就是该区间内得到的最大金币数量，以此类推，最后就能推出整个数组范围为开区间时最后戳爆区间内中间任意一个气球k的所有情况的最大值就是本题所要的结果

代码

class Solution {
    public int maxCoins(int[] nums) {
        // 临时数组方便处理左右边界越界问题
        int oldLen = nums.length;
        int[] tmpArr = new int[oldLen + 2];
        tmpArr[0] = 1;
        for (int i = 1; i <= oldLen; i++) {
            tmpArr[i] = nums[i - 1];
        }
        tmpArr[oldLen + 1] = 1;
        int n = oldLen + 2;
        int[][] dp = new int[n][n];
        // i表示区间范围大小
        for (int i = 3; i <= n; i++) {
            // j表示左区间位置
            for (int j = 0; j <= n - i; j++) {
                int res = 0;
                // k表示最后戳爆的气球位置
                for (int k = j + 1; k < i + j - 1; k++) {
                    res = Math.max(res, dp[j][k] + tmpArr[j] * tmpArr[k] * tmpArr[i + j - 1] + dp[k][i + j - 1]);
                }
                dp[j][i + j - 1] = res;
            }
        }
        return dp[0][n - 1];
    }
}