数据挖掘课程设计报告总结

一、实验题目

实验一 Apriori算法设计与应用

二、背景介绍

Apriori算法是一种挖掘关联规则的频繁项集算法，其核心思想是通过候选集生成和向下封闭检测两个阶段来挖掘频繁项集。

三、实验内容

1.3.1 运用的理论知识

关联规则挖掘是数据挖掘中最活跃的研究方法之一，最初的动机是针对购物篮分析问题提出的，其目的是为了发现交易数据库中不同商品之间的练习规则。通过用户给定的最小支持度，寻找所有频繁项目集，即满足Support不小于Minsupport的所有项目子集。通过用户给定的最小可信度，在每个最大频繁项目集中，寻找Confidence不小于Minconfidence的关联规则。
支持度：支持度就是几个关联的数据在数据集中出现的次数占总数据集的比重。或者说几个数据关联出现的概率。
置信度：置信度体现了一个数据出现后，另一个数据出现的概率，或者说数据的条件概率。

1.3.2 实验原理

Apriori算法基本思想：
首先扫描数据库中所需要进行分析的数据，在设置完支持度以及置信度以后，在最小支持度的支持下产生频繁项，即统计所有项目集中包含一个或一个以上的元素频数，找出大于或者等于设置的支持度的项目集。其次就是频繁项的自连接。再者是如果对频繁项自连接以后的项的子集如果不是频繁项的话，则进行剪枝处理。接着对频繁项处理后产生候选项。最后循环调用产生频繁项集。

1.3.3 算法详细设计

（1）定义数据集、最小支持度、最小支持数、最小置信度以及存放所有频繁项目集的Map集合。调用就封装好的initDataList()方法对数据进行初始化。
（2）调用getAllElement()方法获取到数据集所含有的所有类别元素allElement，将allElement数组进行排列组合获取候选集candidateL1。调用getItemSets()方法遍历candidateL1，将出现次数不小于最小支持数minSupportCount的项加入到itemSets中，遍历结束，获取到1-频繁项目集L1，并将L1打印输出。
（3）开始循环找k-频繁项目集，直到得到的k-频繁项目集Lk为空，跳出循环。在循环体内部，将k-1-候选集candidateLast所含有的所有类别元素allElementLast作为参数调用getCombination()方法，获取k-候选集candidateNow，遍历k-候选集，将出现次数不小于最小支持数的项加入到itemSets并返回，得到频繁项目集Lk。如果k-频繁项集为空，则结束循环，若Lk不为空，则将Lk加入到存放所有频繁项目集allItemSets的集合中，方便之后找强关联规则。
（4）调用correlation()方法进行强关联规则的挖掘。在方法体内部，遍历所有的频繁项目集，得到每一项频繁项目集的非空子集集合subSet，遍历每一项频繁项目集的非空子集，以此非空子集和此频繁项目集作为参数，调用isConfidence()方法判断是否满足置信度大于最小置信度，若满足，则输出此非空子集==>非空子集的补集。

1.3.4 关键源代码

/**
 * 获取候选集
 * @param allItemStr 含频繁项目集所有元素的数组
 * @param k 要生成k候选集
 * @return
 */
public static List<String[]> getCombination(String[] allItemStr, int k){
    //定义候选集
    List<String[]> candidateSets = new ArrayList<>();
    //对allItemStr进行k组合
    IGenerator<List<String>> candidateList = Generator.combination(allItemStr).simple(k);
    for (List<String> candidate : candidateList) {
        String[] candidateStr = candidate.toArray(new String[candidate.size()]);
        candidateSets.add(candidateStr);//将每一项组合放入候选集中
    }
    return candidateSets;
}
/**
 * 处理候选集，获取频繁项目集
 * @param itemList 候选集
 * @return 频繁项目集
 */
public static Multimap<Integer, String[]> getItemSets(List<String[]> itemList){
    Multimap<Integer, String[]> itemSets = ArrayListMultimap.create(); //项目集
    //得到排列组合结果（候选集）每一项在数据集中出现的次数
    Multimap<Integer, String[]> itemCount = getItemCount(itemList);
    //使用迭代器遍历multimap
    Iterator<Map.Entry<Integer, String[]>> iterator = itemCount.entries().iterator();
    //遍历排列组合结果的每一项，将出现次数不小于minSupportCount的项加入到itemSets
    while (iterator.hasNext()){
        Map.Entry<Integer, String[]> entry = iterator.next();
        if (entry.getKey() >= minSupportCount){
            itemSets.put(entry.getKey(), entry.getValue());
        }
    }
    return itemSets;
}
/**
 * 找强关联规则
 */
public static void correlation(){
    //遍历所有频繁项目集
    for (int k = 1; k <= allItemSets.size(); k++) {
        //获取k-频繁项目集
        Multimap<Integer, String[]> keyItemSet = allItemSets.get(k);
        Iterator<Map.Entry<Integer, String[]>> iterator = keyItemSet.entries().iterator();
        //遍历k频繁项目集
        while (iterator.hasNext()){
            Map.Entry<Integer, String[]> entry = iterator.next();
            String[] value = entry.getValue();
//                List<String> valueList = Arrays.asList(value);
//                List<String> valueList = new ArrayList<>();
//                Collections.addAll(valueList, value);
            //求value的非空子集
            for (int i = 1; i < value.length; i++) {
                List<String[]> subSet = getCombination(value, i); //非空子集的集合
                for (String[] subSetItem : subSet) { //subSetItm是频繁项目集每一个非空子集
                    List<String> valueList = new ArrayList<>();
                    Collections.addAll(valueList, value);
                    List<String> subSetItemList = Arrays.asList(subSetItem);
                    //去除已经求得子集后的valueList
                    valueList.removeAll(subSetItemList); //此时valueList中存放非空子集的补集
                    if (isConfidence(subSetItem, value)){
                        System.out.println(Arrays.toString(subSetItem) + "==>" + Arrays.toString(valueList.toArray(new String[valueList.size()])));
                    }
                }
            }
        }
    }
}

四、实验结果与分析

1.4.1 测试代码

public static void main(String[] args) {
    // 初始化数据集
    initDataList();
    String[] allElement = getAllElement(dataList);
    //获取候选集L1
    List<String[]> candidateL1 = getCombination(allElement, 1);
    Multimap<Integer, String[]> itemSetsL1 = getItemSets(candidateL1);
    allItemSets.put(1, itemSetsL1);
    printResult(itemSetsL1, 1);
    List<List<String[]>> stack = new ArrayList<>();
    stack.add(candidateL1);
    for (int k = 2; true; k++) {
        List<String[]> candidateLast = stack.get(0);
        String[] allElementLast = getAllElement(candidateLast);
        List<String[]> candidateNow = getCombination(allElementLast, k);
        Multimap<Integer, String[]> itemSetsLk = getItemSets(candidateNow);
        if (itemSetsLk.isEmpty()) break;
        allItemSets.put(k, itemSetsLk);
        printResult(itemSetsLk, k);
        stack.remove(0);
        stack.add(candidateNow);
    }
    correlation();
}

1.4.2 测试结果

在这里插入图片描述

由于所有强关联规则实在是太多了，这里只展示部分强关联规则，如图1-4-2所示：

在这里插入图片描述

最后得到的所有频繁项目集中，最大频繁项目集5-频繁项目集。由于不知道结果是否正确，我将有正确答案的数据集输入后进行了测试，输出结果是没什么问题的。感觉本实验给出的置信度和支持度太小了，或者说给出的数据集中，每一项所包含的数据元素种类重合度都太高了，导致强关联规则太多，甚至每一项关联规则的置信度都大于了最小置信度。

五、小结与心得体会

本实验是用Java语言实现的，我认为哪种语言实现的并不重要，重要的是理解算法的基本思想和实现原理，Apriori算法作为数据挖掘的十大经典算法之一，掌握其算法思想是十分重要的。本次实验用Java语言实现，总计260行，我自认为部分代码写的还是有些冗余，可以再精简些。
本次实验的实现可圈可点的是在找候选集时，笔者没有用常规算法思路去求得数组的排列组合，而是利用combinatorics3依赖中的combination()方法，传入含所有数据元素种类的数组和k值，直接可以得到数组的k组合结果。另外，本实验的实现中还用到了谷歌的guava依赖中的Multimap集合，Multimap集合可以存放key值重复的键值对，方便了存储候选集和其在数据集中出现的次数。

一、实验题目

实验五 KNN算法设计与应用

二、背景介绍

k-近邻（kNN, k-NearestNeighbor）是在训练集中选取离输入的数据点最近的k个邻居，根据这个k个邻居中出现次数最多的类别（最大表决规则），作为该数据点的类别。

三、实验内容

2.3.1 运用的理论知识

分类在数据挖掘中是一项非常重要的任务。分类的目的是学会一个分类函数或分类模型（也常常称作分类器），该模型能把数据库中的数据项映射到给定类型中的某一个类别。分类可用于预测。预测的目的是从历史数据记录中自动推导出对给定数据的趋势描述，从而能对未来数据进行预测。统计学中常用的预测方法是回归。数据挖掘中的分类和统计学中的回归方法是一对相互联系又有区别的概念。一般地，分类的输出是离散的类别值，而回归的输出则是连续数值。
给定一个数据库D={t1,t2,…,tn}和一组类C={C1,C2,…,Cm}。对于任意的元组ti={ti1,ti2,…,tik}∈D，如果存在一个Cj∈C，使得sim(ti,Cj)≥sim(ti,Cp)，存在Cp∈C，Cp≠Cj，则ti被分配到类Cj中，其中sim(ti,Cj)称为相似性。
在实际的计算中往往用距离来表征，距离越近，相似性越大，距离越远，相似性越小。
为了计算相似性，需要首先得到表示每个类的向量。计算方法有多种，例如代表每个类的向量可以通过计算每个类的中心来表示。另外，在模式识别中，一个预先定义的图像用于代表每个类，分类就是把待分类的样例与预先定义的图像进行比较。

2.3.2 实验原理

KNN算法基本思想：
KNN算法的思想比较简单。假定每个类包含多个训练数据，且每个训练数据都有一个唯一的类别标记，KNN算法的主要思想就是计算每个训练数据到待分类元组的距离，取和待分类元组距离最近的k个训练数据，k个数据中哪个类别的训练数据占多数，则待分类元组就属于哪个类别。

2.3.3 算法详细设计

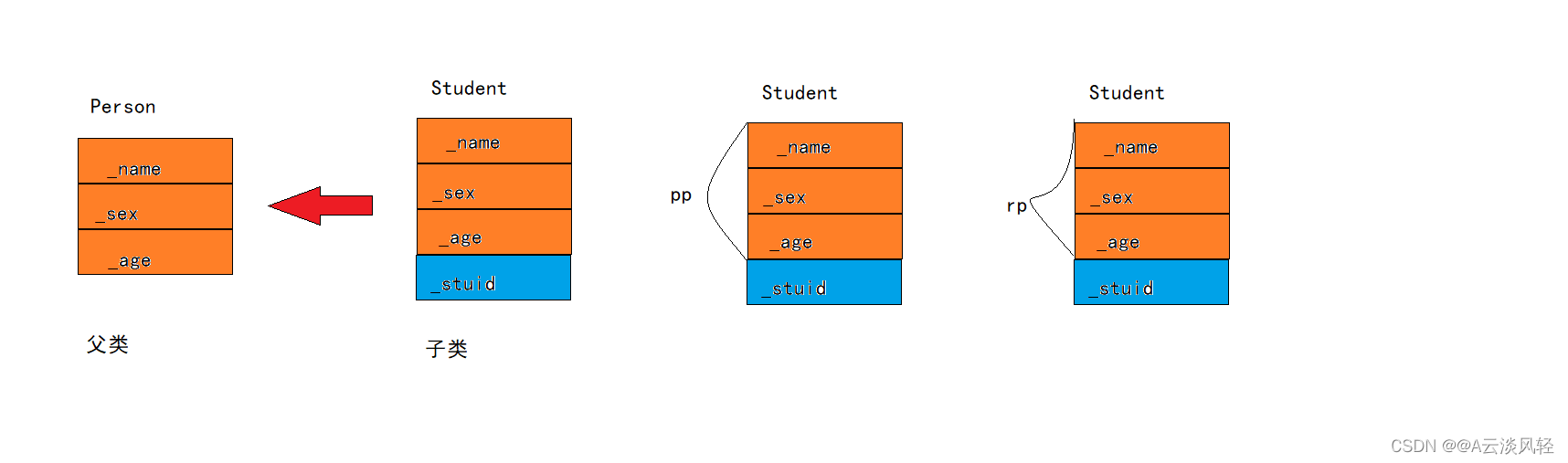
（1）定义学生类Student，学生类中定义姓名，身高，等级等属性，利用lombok依赖的@Data注解对Student类的get和set方法进行注入。定义初始数据集，定义14个实体学生类，将14个实体Student类添加到初始数据集dataList中。
（2）调用initData()方法对数据集进行初始化，定义一个Student类stuV0并对其姓名和身高进行实例化作为输入，调用Knn()方法，得到含有等级的Student类对象student，将对象student进行输出。
（3）在Knn()方法体内部，初始时将数据集的前5项加入到categoryList集合中，categoryList集合用于存放距离stuV0最近的k个学生，只是最初存放数据集的前5项而已。遍历数据集dataList，计算stuV0距离从数据集的第6项开始的每一项的距离v0Tod，另外调用getCalculate()方法计算出stuV0距离categoryList集合中最远的学生对象stuU，若stuU距离stuV0的身高距离uToV0大于v0Tod，则在categoryList中去除掉stuU，将数据集中的该项加入到categoryList集合中来。
（4）在getCalculate()方法体内部，定义变量maxHeight用于存放stuV0与类别集合categoryList的最远距离，定义Student类对象resultStu用于存放要返回的学生，即stuV0与类别集合categoryList距离最远的学生。遍历categoryList集合，若stuU与stuV0之间的距离大于maxHeight，则将v0ToU赋值给maxHeight，将stuU赋值给resultStu，最终将Student类对象resultStu返回。
（5）调用getCategoryStudent()方法找出categoryList中同等级占比最多的学生等级rank，最终用rank实例化stuV0的rank属性，返回stuV0。
（6）在getCategoryStudent()方法体内部，遍历categoryList，找出同等级占比最多的学生等级，其实就是找等级“高”、等级“中等”，等级“矮”的学生哪个类别的学生数量最多，并将学生数量最多的那个类别返回。

2.3.4 关键源代码

/**
 * 对输入学生类进行Knn算法实例化该学生的等级后，将该学生返回
 * @param stuV0
 * @return
 */
public static Student Knn(Student stuV0){
    List<Student> categoryList = new ArrayList<>(); //存放距离stuV0最近的k个学生，最初存放数据集的前5项
    for (int i = 0; i < dataList.size(); i++) {
        if (i < 5) categoryList.add(dataList.get(i));
        else {
            //stuV0距离剩下数据集中某项的距离
            int v0Tod = Math.abs(stuV0.getHeight() - dataList.get(i).getHeight());
            Student stuU =  getCalculate(stuV0, categoryList); //存放stuV0距离类别集合中最远的学生
            int uToV0 = Math.abs(stuU.getHeight() - stuV0.getHeight());
            if (uToV0 > v0Tod){
                categoryList.remove(stuU); //在集合列表中去除stuU
                categoryList.add(dataList.get(i));
            }
        }
    }
    System.out.println(categoryList.toString());
    String rank = getCategoryStudent(categoryList);
    stuV0.setRank(rank);
    return stuV0;
}
/**
 * 计算出stuV0距离categoryList集合中最远的学生对象
 * @param stuV0
 * @param categoryList
 * @return
 */
public static Student getCalculate(Student stuV0, List<Student> categoryList) {
    int maxHeight = 0; //存放stuV0与类别集合categoryList的最远距离
    Student resultStu = new Student(); //存放要返回的学生，即stuV0与类别集合categoryList距离最远的学生
    for (Student stuU : categoryList) {
        int v0ToU = Math.abs(stuV0.getHeight() - stuU.getHeight()); //stuV0与stuU的距离
        if (v0ToU > maxHeight){ //stuV0与stuU的距离大于maxHeight，则对maxHeight和resultStu进行更新
            maxHeight = v0ToU;
            resultStu = stuU;
        }
    }
    return resultStu;
}
/**
 * 找出同等级占比最多的学生等级
 * @param categoryList
 * @return
 */
public static String getCategoryStudent(List<Student> categoryList){
    int tallCount = 0;
    int midCount = 0;
    int smallCount = 0;
    for (Student stuU : categoryList) {
        if (stuU.getRank().equals("高")) tallCount++;
        else if (stuU.getRank().equals("中等")) midCount++;
        else smallCount++;
    }
    int max = 0;
    max = tallCount > midCount ? tallCount : midCount;
    max = smallCount > max ? smallCount : max;
    if (smallCount == max) return "矮";
    else if (tallCount == max) return "高";
    else return "中等";
}

四、实验结果与分析

2.4.1 测试代码

public static void main(String[] args) {
    initData();
    Student stuV0 = new Student("易昌", 174);
    Student student = Knn(stuV0);
    System.out.println(student.toString());
}

2.4.2 测试结果

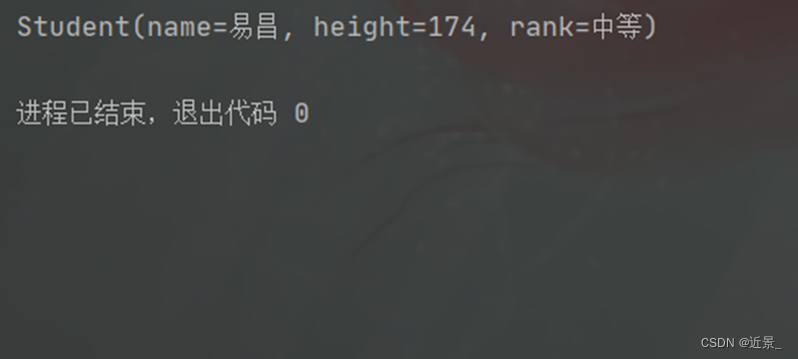
在这里插入图片描述
另外，除了输出题目要求的学生身高等级外，笔者还输出了输入学生所在的簇，以对照题目确保结果正确。

最后得到的身高为174的同学易昌，其身高等级为中等，其所在的簇中所有学生也如上表2-4-1所示。依笔者所见，这个数据集和输入数据给的也不好，这最终的簇中都是身高等级为“中等”的同学，那易昌同学自然也为“中等”了，感觉如果最终簇中有3个身高等级为中等的同学，2个身高等级为高的同学，感觉这样的数据集更有代表性，更能体现KNN算法的思想吧。

五、小结与心得体会

本实验是用Java语言实现的，感觉KNN算法的实现思路还是挺简单的，个人认为比Apriori算法的实现要简单太多，当然也有可能是笔者把Apriori算法写的复杂了。KNN算法作为数据挖掘的十大经典算法，对于学习数据挖掘中的分类思想有着很大的帮助，总代码行122行，这个算法还创建了Student类，用上了Java面向对象的编程思想。
本实验的实现过程当中还是遇到了一些问题，比如对getCategoryStudent()方法的实现，其实该方法的实现本身并不困难，就是遍历几个数找最大值而已，当时笔者思路是想找一下看看有没有Java封装好的类库直接使用的，结果找了半天也无所获，就自己写了。这里也算有个小小的比较有意思的点，就是最后找三个数最大值时没有用常规的if判断，而是使用了三目运算符，这是出于找最值这个过程并不困难，代码阅读性还算简洁，所以才用了三目运算符，但是过程难懂的代码个人认为还是用if判断好一些，可以增加代码可读性。
通过完成本实验，读者对于KNN分类算法有了进一步的了解和认识，能够更熟练地运用Java语言，对于Java面向对象的编程思想有了更进一步的理解。

一、实验题目

实验七 DBSCAN算法设计与应用

二、背景介绍

DBSCAN算法：如果一个点q的区域内包含多于MinPts个对象，则创建一个q作为核心对象的簇。然后，反复地寻找从这些核心对象直接密度可达的对象，把一些密度可达簇进行合并。当没有新的点可以被添加到任何簇时，该过程结束。

三、实验内容

3.3.1 运用的理论知识

DBSCAN是一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在有“噪声”的空间数据库中发现任意形状的聚类。聚类就是将数据对象分组成为多个类或簇，划分的原则是在同一个簇中的对象之间具有较高的相似度，而不同簇中的对象差别较大。与分类不同的是，聚类操作中要划分的类是事先未知的，类的形成完全是数据驱动的，属于一种无指导的学习方法。
对象的ε-领域：给定对象在半径ε内的区域。
核心对象：如果一个对象的ε-领域至少包含最小数目MinPts个对象，则称该对象为核心对象。
直接密度可达：给定一个对象集合D，如果p是在q的ε-领域内，而q是一个核心对象，我们说对象p从对象q出发是直接密度可达的。
密度相连的：如果对象集合D中存在一个对象o，使得对象p和q是从o关于ε和MinPts密度可达的，那么对象p和q是关于ε和MinPts密度相连的。

3.3.2 实验原理

DBSCAN算法基本思想：
DBSCAN是一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在有“噪声”的空间数据库中发现任意形状的聚类。
从数据库中抽取一个未处理过的点，如果抽出的点是核心点，那么找出所有从该点密度可达的对象，形成一个簇；如果抽出的点是边缘点（非核心对象），跳出本次循环，寻找下一点，直到所有点都被处理。

3.3.3 算法详细设计

（1）定义Point类，Point类中含横坐标x，纵坐标y等属性，包含静态方法getIsSame()：判断两个Point类对象是否相同、calculateDistance()方法：计算两个Point类对象之间的距离（欧氏距离）、calculateMHDDistance()方法：计算两个Point类对象之间的距离（曼哈顿距离）。定义ExcelData类，ExcelData类中包含横坐标x（添加注解@ExcelProperty(value=“横坐标”)），纵坐标y（添加注解@ExcelProperty(value=“纵坐标”)），ExcelData类主要用于读取excel文件的数据映射到ExcelData类中。定义Cluster类，在Cluster类中包含属性核心点corePoint，簇内的所有点的集合sameList。
（2）定义初始数据集dataList，定义半径e，定义核心对象e领域内对象的最少数目MinPts，调用getFileData()方法对初始数据集进行初始化。在getFileData()方法体内部使用EasyExcel对excel文件进行读取并映射到ExcelData类对象中，将ExcelData类对象中的属性x和属性y作为构造参数，实例化出Point类对象point，并将所有的point添加到dataList集合中，完成对数据集的初始化。
（3）创建clusterList集合，用于存放所有的簇。遍历dataList集合中的每一个Point类对象point，在循环体内部，调用getEPointList()方法获取一个Point类对象领域内所有的点集合ePointList，如果ePointList集合的长度不小于MinPts，说明点point是核心对象，则实例化一个以point为核心对象的簇cluster，并用ePointList实例化簇cluster的sameList属性，然后调用canReachPoint()方法遍历核心对象直接密度可达的点，合并其所有密度可达的点，将最终的簇newCluster加入到簇集合newCluster中。在循环体内部首先调用isExitCluster()方法判断是否点已经存在于某个簇中，已经在簇中的点则不再考虑，不再执行循环体内接下来的代码，直接开始遍历下一次循环，直到遍历过dataList集合中的每一项后，循环结束。
（4）遍历clusetrList集合，将集合中的每一项cluster输出即可。
（5）在isExistCluster()方法体内部，判断point对象是否已经在已存在的簇中，遍历clusterList集合中的每一个簇cluster，获取簇cluster中的sameList属性，判断其sameList集合中是否含point，若含有则返回true。遍历结束后，返回false。
（6）在canReachPoint()方法体内部，遍历簇cluster中包含的所有点，判断除核心对象点以外的每一个点point是否是核心对象，若point也是核心对象，则其领域内所有的点是簇cluster核心点的密度可达的点，也可以合并到簇cluster中，将这些点添加到密度可达的点集合reachPointList中，当循环结束后，将集合reachPointList中所有的密度可达的点加入到簇的sameList集合中，重新实例化簇cluster，最终将cluster返回。
（7）getEpointList()方法的作用是获取一个点e领域内所有点的集合。在方法体内部，定义点集合pointList用于存放point的e领域内所有的点，遍历数据集dataList中的每一个点p，调用Point类内的静态方法calcuteMHDDistance()方法，计算点point和点p的曼哈顿距离，用变量ptoPoint来存放，如果ptoPoint小于半径e，则说明点p在点point的e领域内，则将p加入到pointList集合当中，最终返回pointList集合。

3.3.4 关键源代码

/**
 * 判断point是否已经在已存在的簇中
 * @param point
 * @param clusterList
 * @return
 */
public static boolean isExistCluster(Point point, List<Cluster> clusterList){
    for (Cluster cluster : clusterList) {
        List<Point> pointList = cluster.getSameList();
        if (pointList.contains(point)) return true;
    }
    return false;
}
/**
 * 遍历核心对象直接密度可达的点，合并其所有密度可达的点
 * @param cluster
 * @return
 */
public static Cluster canReachPoint(Cluster cluster){
    List<Point> pointList = cluster.getSameList();
    List<Point> reachPointList = new ArrayList<>(); //存放核心点所有密度可达的点（暂存要新加入进来的点）
    for (Point point : pointList) {
        Point corePoint = cluster.getCorePoint();
        if (Point.getIsSame(corePoint, point)) continue; //这里不再遍历核心对象点
        List<Point> reachList = getEPointList(point); //核心对象直接密度可达的点其e领域内所有的点的集合
        if (reachList.size() >= MinPts){ //说明point也是核心对象，其领域内的所有点也可以合并到cluster中
            for (Point reachPoint : reachList) {
                if (pointList.contains(reachPoint)) continue; //对于pointList中已经有的点不再重复添加
                reachPointList.add(reachPoint); //将密度可达的点添加到密度可达的点集合中
            }
        }
    }
    pointList.addAll(reachPointList); //将密度可达的点全加入到簇中
    cluster.setSameList(pointList);
    return cluster;
}
/**
 * 获取一个点的e领域内所有的点集合
 * @param point
 * @return
 */
public static List<Point> getEPointList(Point point){
    List<Point> pointList = new ArrayList<>(); //存放point的e领域内所有的点
    for (Point p : dataList) {
        double ptoPoint = Point.calculateMHDDistance(point, p);
        if (ptoPoint <= e) pointList.add(p); //说明点p在point的e领域内
    }
    return pointList;
}
四、实验结果与分析
3.4.1 测试代码
public static void main(String[] args) {
    getFileData();
//        initDataList();
    List<Cluster> clusterList = new ArrayList<>();
    for (Point point : dataList) {
        if (isExistCluster(point, clusterList)) continue; //已经在簇中的点不再考虑
        List<Point> ePointList = getEPointList(point);
        if (ePointList.size() >= MinPts){ //说明点point是核心对象
            Cluster cluster = new Cluster(point);
            cluster.setSameList(ePointList);
            Cluster newCluster = canReachPoint(cluster);
            clusterList.add(newCluster);
        }
    }
    int pointSum = 0;
    for (Cluster cluster : clusterList) {
        System.out.println(cluster);
        pointSum += cluster.getSameList().size();
    }
    System.out.println(pointSum);
}

3.4.2 测试结果

在这里插入图片描述

其实看到输出后笔者是十分疑惑的，感觉输出的聚类簇内的点数量是不够的，然后就把簇内点的数量进行了输出，结果是聚类了的点有27个，本实验给了63个实验样本点，结果聚类的点只有27个，难道其他36个样本点全是噪声样本点？笔者担心是代码有问题，又测试了下书本上的DBSCAN算法的例子，使用书本上的数据集后对照书上的答案是没问题的。然后笔者又检查了下63个样本数据点，发现有些点是重复点，然后单元测试了下，63个样本点中不重复的点有多少个，并把这个结果进行了输出，结果只有36个样本点是不重复的，也就是说63个样本点里有27个样本点都是完全一样的。
在这里插入图片描述
最后得到的结果簇集合中一共有8个簇，簇中所包含的点的数目为27个，笔者看了下最后的结果，簇中也有一些点是重复的，我一度怀疑是不是代码有问题，调试了几次也没发现什么问题，可能是数据集有点奇葩，半径e和核心对象领域内点的最少数目MinPts给的也不太好吧。

五、小结与心得体会

本实验是用Java语言实现的，DBSCAN算法给我的感觉是一只纸老虎，其实这个实验是放在最后写的，当时感觉数据集样本点给了63个，像前几个实验一样一个个创建实体对象，然后把实体对象添加到数据集集合中并不现实，肯定是要把样本点数据用txt文本或excel表格存放，然后是要用代码读取存放到dataList数据集中的。因为还要处理数据，笔者就放到了最后写，最先为了保证把更多的时间花费在思考DBSCAN的代码实现思路上，就先用了书本上的例子（因为书本上这个例子初始数据集样本点比较少，而且还有答案）。
在实现过程中，发现代码思路并不想刚开始想的那样困难，但还是遇到了一些问题，比如在实现canReachPoint()方法时，直到运行报错时才发现此方法实现过程中的bug，在最初实现时，遍历pointList集合并把密度可达的点直接加入到了pointList集合中，这直接改变了pointList集合的长度，但此时正在for循环遍历期间，运行调试发现bug后，笔者在遍历前定义了reachPointList集合用来存放核心点所有密度可达的点，等遍历pointList集合循环结束后，在调用list的addAll()方法将reachPointList中包含的所有密度可达的点加入到pointList集合，这样做很好地规避了这个bug，代码也顺利执行成功。
通过本次实验，笔者对DBSCAN算法的代码实现思路有了更进一步的认识，对Java语言集合的运用更加地熟练了。

一、实验题目

实验八 K-means算法设计与应用

二、背景介绍

k-means算法，也被称为k-平均或k-均值，是一种得到最广泛使用的聚类算法。相似度的计算根据一个簇中对象的平均值来进行。算法首先随机地选择k个对象，每个对象初始地代表了一个簇的平均值或中心。对剩余的每个对象根据其与各个簇中心的距离，将它赋给最近的簇。然后重新计算每个簇的平均值。这个过程不断重复，直到准则函数收敛。

三、实验内容

4.3.1 运用的理论知识

聚类就是将数据对象分组成多个类或簇，划分的原则是在同一个簇中的对象之间具有较高的相似度，而不同簇中的对象差别较大。与分类不同的是，聚类操作中要划分的类是事先未知的，类的形式完全是数据驱动的，属于一种无指导的学习方法。
聚类分析源于许多研究领域，包括数据挖掘、统计学、机器学习、模式识别等。它是数据挖掘中的一个功能，但也能作为一个独立的工具来获得数据分布的情况，概括出每个簇的特点，或者集中注意力对特定的某些簇作进一步分析。此外，聚类分析也可以作为其他分析算法（如关联规则、分类等）的预处理步骤，这些算法在生成的簇上进行处理。
聚类：聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程，聚类就是一种发现这种内在结构的技术，聚类技术经常被称为无监督学习。
K-means聚类：K-means聚类是最著名的划分聚类算法，由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k，k由用户指定，k均值算法根据某个距离函数反复把数据分入k个聚类中。

4.3.2 实验原理

K-means聚类算法基本思想：
K-means聚类算法是先随机选取K个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了，每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚类，没有(或最小数目)聚类中心再发生变化，误差平方和局部最小。

4.3.3 算法详细设计

（1）定义Point类，Point类中含横坐标x，纵坐标y等属性，包含静态方法getIsSame()：判断两个Point类对象是否相同、calculateDistance()方法：计算两个Point类对象之间的距离（欧氏距离）、calculateMHDDistance()方法：计算两个Point类对象之间的距离（曼哈顿距离）。定义Cluster类，在Cluster类中包含属性核心点corePoint，簇内的所有点的集合sameList。
（2）定义初始数据集dataList，定义簇的数目k，调用initDataList()方法进行初始化数据集，调用getInitCluster()方法进行初始化簇。getInitCluster()方法主要作用是获取任意k个对象作为初始簇中心，将含有k个簇的集合返回。在getInitCluster()方法体内部，定义clusterList集合用于存放k个簇，调用getRandomArray()方法获取含有k个不重复随机数的数组randomArray，数据集中k个对象的下标存放在randomArray数组中，遍历数组randomArray，取出k个任意下标的Point类对象作为相应簇cluster的核心对象点，并将每一次循环定义和实例化后的cluster添加到clusterList中，最终将clusterList集合返回。
（3）进入while循环，遍历数据集dataList中的每一项point，调用getBelongCluster()方法获取point属于的那个簇在clusterList中的下标index，取出clusterList中指定下标index的簇，将点point加入到该簇的sameList中。然后遍历数据集结束后，调用calculateClusterCore()方法计算出新的簇中心并判断出簇集合中每个簇的点集合是否有发生变化，若未发生变化，则跳出while循环，表明K-means聚类结束，反之则进入下次while循环，在遍历数据集之前，要将clusterList集合中的每一项cluster的sameList集合清空。
（4）遍历clusetrList集合，将集合中的每一项cluster输出即可。
（5）getBelongCluster()方法主要作用是获取某个点属于哪个簇的下标。在方法体内部，定义了变量closestDistance和变量resultClusterIndex分别用于存放point距离簇中心最近的距离，以及point属于的哪个簇的下标。遍历簇集合clusterList，调用Point类内静态方法calculateDistance()计算点point距离簇cluster核心点的距离赋值给distance，将第一次遍历得到的distance值赋值给cloestDistance，后面的遍历如果distance小于closestDistance，就将distance赋值给closestDistance，同时将index赋值给resultClusterIndex，循环遍历结束，最终将resultClusterIndex返回。
（6）calculateClusterCore()方法主要作用是计算出新的簇中心并返回簇的点集合是否有变化。在方法体内部定义标志变量flag，然后遍历clusterList集合中的每一项cluster，定义变量sumX和变量sumY分别用于存放簇中点集合所有的x坐标之和，以及簇中点集合所有的y坐标之和，对sumX和sumY求均值后赋值给新的簇中心点clusterCore，调用Point类内静态方法getIsSame()判断clusterCore和原簇中心是否相同，若不相同则将flag赋值为true。当遍历簇集合循环结束后，将flag值返回。要注意的是这里形参类型是List集合，传的是List集合的地址，在方法体内对集合进行修改则会导致实参的值也发生改变。

4.3.4 关键源代码

/**
 * 计算出新的簇中心并返回簇的点集合是否有变化
 * @param clusterList
 * @return
 */
public static boolean calculateClusterCore(List<Cluster> clusterList){
    boolean flag = false;
    //遍历簇集合中的每一项，更新其簇中心
    for (Cluster cluster : clusterList) {
        List<Point> sameList = cluster.getSameList();
        double sumX = 0; //存放簇中点集合所有的X坐标之和
        double sumY = 0; //存放簇中点集合所有的Y坐标之和
        for (Point point : sameList) {
            sumX += point.getX();
            sumY += point.getY();
        }
        //更新簇的中心
        Point clusterCore = new Point(sumX * 1.0 / sameList.size(), sumY * 1.0 / sameList.size());
        if (!Point.getIsSame(clusterCore, cluster.getCorePoint())) flag = true;
        cluster.setCorePoint(clusterCore);
    }
    return flag;
}
/**
 * 获取某个点属于哪个簇的下标
 * @param point
 * @return
 */
public static int getBelongCluster(Point point, List<Cluster> clusterList){
    double closestDistance = 0.0; //存放point距离簇中心最近的距离
    int resultClusterIndex = 0; //存放point属于的那个簇的下标
    int index = 0;
    //遍历簇集合，计算point到簇中心的距离，找出point属于的簇
    for (Cluster cluster : clusterList) {
        double distance = Point.calculateDistance(point, cluster.getCorePoint());
        if (index == 0) closestDistance = distance;
        if (distance < closestDistance){
            closestDistance = distance;
            resultClusterIndex = index;
        }
        index++;
    }
    return resultClusterIndex;
}
/**
 * 获取任意k个对象作为初始簇中心，将含有k个簇的集合返回
 * @return
 */
public static List<Cluster> getInitCluster(){
    List<Cluster> clusterList = new ArrayList<>();
    int[] randomArray = getRandomArray();
    //任意选取k个对象作为初始簇中心，数据集中k个对象的下标存放在randomArray中
    for (int i = 0; i < randomArray.length; i++) {
        Point point = dataList.get(randomArray[i]);
        Cluster cluster = new Cluster(point);
        clusterList.add(cluster);
    }
    return clusterList;
}

四、实验结果与分析

4.4.1 测试代码

public static void main(String[] args) {
    //初始化数据集和初始簇
    initDataList();
    List<Cluster> clusterList = getInitCluster();
    while(true){
        for (int j = 0; j < k; j++) {
            clusterList.get(j).getSameList().clear();
        }
        for (Point point : dataList) {
            int index = getBelongCluster(point, clusterList); //获取point属于的那个簇在clusterList中的下标
            clusterList.get(index).getSameList().add(point); //把point加入到clusterList的对应簇中;
        }
        if (!calculateClusterCore(clusterList)) break;
    }
    for (Cluster cluster : clusterList) {
        System.out.println(cluster);
    }
}

4.4.2 测试结果

在这里插入图片描述

输出结果无疑是3个簇，因为k的值就为3。这里笔者进行了多次测试，发现随着测试次数增多，会出现测试结果不同的情况，在搜集过资料后，笔者个人认为这种情况是正常的，原因是由于初始时是随机选取的簇中心点，可能开始选取的簇中心点位置过于紧凑或者过于疏散，都会影响到最后的输出结果，经过多次测试后，笔者发现有一组输出结果的出现频率是最高的，这组输出结果如图4-4-1所示。
在这里插入图片描述
最后得到的结果看上去也算正常，这里对于初始化簇的集合，笔者是在0-12之间随机选取了3个数，为了避免选取的3个数重复，笔者还使用了while循环，直到取到下标集合中不含的下标为止，再进入下次取数，最后经过多次调试后，暂时没发现什么bug，至于多次测试出现的一些结果不同的输出，笔者认为也是正常的。

五、小结与心得体会

本实验是用Java语言实现的，K-means聚类算法是数据挖掘的十大经典算法之一，在实现过程中，也遇到了一些问题。在使用List集合作为方法参数时，笔者本想使用oldClusterList暂存传参前的clusterList集合，使用newClusterList暂存传参后的clusterList集合，最初忽略了List集合作为方法参数时传的是集合地址，方法体内改变集合内容，则实参集合内容也会改变，在后续的调试中，笔者才发现了这一问题，对其进行了订正。
通过这次实验，笔者对K-means聚类算法有了更进一步的了解，本实验最好的是可以让点集合可视化，这样就可以更清晰地看到聚类结果，由于时间原因，没有对其进行可视化处理，后面有精力和时间了可能对其进行更新。

一、实验题目

实验九 PageRank算法设计与应用

二、背景介绍

PageRank算法：计算每一个网页的PageRank值，然后根据这个值的大小对网页的重要性进行排序。

三、实验内容

5.3.1 运用的理论知识

从用户角度来看，一个网站就是若干页面组成的集合。然而，对于网站的设计者来说，这些页面是经过精心组织的，是通过页面的链接串联起来的一个整体。因此，Web的结构挖掘主要是对网站中页面链接结构的发现。例如：在设计搜索引擎等服务时，对Web页面的链接结构进行挖掘可以得出有用的知识来提高检索效率和质量。
一般来说，Web页面的链接类似学术上的引用，因此，一个重要的页面可能会有很多页面的链接指向它。也就是说，如果有很多链接指向一个页面，那么它一定是重要的页面。同样地，假如一个页面能链接到很多页面，它也有其重要的价值。
设u为一个Web页，Bu为所有指向u的页面的集合，Fu为所有u指向的页面的集合，c（<1）为一个归一化的因子，那么u页面的等级R(u)被定义为：R(u)=c∑_(v∈Bu)▒(R(v))/(|Fv|)，很显然，基本的页面分级方法主要考虑一个页面的入度，即通过进入该页面的页面等级得到。同时，在将一个页面的等级值传递时，采用平均分配方法传递到所有它所指向的页面，即每个从它链接处的页面等分它的等级值。
PageRank算法的核心部分可以从一个有向图开始。最典型的方法是根据有向图构造一个邻接矩阵来进行处理。邻接矩阵A=(ai,j)中的元素ai,j(∈[0,1])表示从页面j指向页面i的概率。

5.3.2 实验原理

PageRank算法基本思想：
基本的PageRank算法在计算等级值时，每个页面都将自己的等级值平均地分配给其引用的页面节点。假设一个页面的等级值为1，该页面上共有n个超链接，其分配给每个超链接页面的等级值就是1/n，那么就可以理解为该页面以1/n的概率跳转到任意一个其所引用的页面上。
一般地，把邻接矩阵A转换成所谓的转移概率矩阵M来实现PageRank算法：M=(1-d)Q+dA，其中，Q是一个常量矩阵，最常用的是Q=(qi,j)，qi,j=1/n，转移概率矩阵M可以作为一个向量变换矩阵来帮助完成页面等级值向量R的迭代计算：Ri+1=M*R

5.3.3 算法详细设计

（1）定义Score分数类，在Score分数类中包含分子son和分母mom属性，还包含静态方法simplify()用于对分子分母进行约分，静态方法getAdd()用于分数相加并化简结果，静态方法getMultiply()用于分数相乘并调用simplify()对结果进行化简。
（2）定义初始数据集dataList，定义转移矩阵的每一项Score分数类对象，调用InitData()方法对数据集进行初始化。
（3）定义Score类对象v0Score并对其实例化，v0Score对象表示分数值1/4，表示最初人们对点击A，B，C，D四个网页的概率都是相同的1/4。定义一维数组V0存放4个v0Score，初始的PageRank也赋值成V0。
（4）进入while循环，调用getPageRank()方法获取PageRank矩阵。在getPageRank()方法体内部定义pageRankList集合存放最终的PageRank值，遍历dataList数据集中每一项数据dataItem，使用for循环遍历dataItem，使得dataItem和Vk完成矩阵乘法，并将矩阵乘法后每一项的结果保存在itemSum当中，当遍历dataItm结束后，将itemSum添加到pageRankList集合当中，在遍历数据集dataList集合结束后，将pageRankList转换成数组后返回。
（5）调用isRankEqual()方法判断新得到的PageRank矩阵值是否和上次得到的PageRank矩阵值相同，若不相同则继续迭代，若相同则不再迭代。isRankEqual()方法主要是判断形参V1和形参V2的PageRank矩阵内的值是否相等，返回boolean类型的值，方法体内部对数组V1进行遍历，比较V1中每一项的分子和V2中每一项的分子是否相同，若有不相同的则返回false，若遍历结束后没有不同的则返回true。
（6）若新得到的PageRank矩阵值不与上次得到的PageRank矩阵值相同，则将新得到的PageRank矩阵值赋值给最终要输出的pageRank变量，输出每一次得到的PageRank值。

5.3.4 关键源代码

/**
 * 判断V1和V2的PageRank矩阵内的值是否相等
 * @param V1
 * @param V2
 * @return
 */
public static boolean isRankEqual(Score[] V1, Score[] V2){
    for (int i = 0; i < V1.length; i++) {
        int subSon = V1[i].getSon() - V2[i].getSon();
        int subMom = V1[i].getMom() - V2[i].getMom();
        if (subSon != 0 || subMom != 0) return false;
    }
    return true;
}
/**
 * 获取PageRank矩阵
 * @param Vk
 * @return
 */
public static Score[] getPageRank(Score[] Vk){
    List<Score> pageRankList = new ArrayList<>();
    for (Score[] dataItem : dataList) {
        Score itemSum = new Score(0,0); //itemSum中存放PageRank矩阵的每一项
        //通过遍历数据集的每一行和Vk的每一列实现矩阵乘法
        for (int i = 0; i < dataItem.length; i++) {
            Score multiply = Score.getMultiply(dataItem[i], Vk[i]);
            itemSum = Score.getAdd(multiply, itemSum); //将对应项相乘的结果累加到itemSum中
        }
        pageRankList.add(itemSum);
    }
    return pageRankList.toArray(new Score[pageRankList.size()]);
}

四、实验结果与分析

5.4.1 测试代码

public static void main(String[] args) {
    initData();
    Score voScore = new Score(1, 4);
    Score[] V0 = {voScore, voScore, voScore, voScore};
    Score[] pageRank = V0;
    while (true){
        Score[] tmpVk = getPageRank(pageRank);
        if (isRankEqual(pageRank, tmpVk)) break; //新得到的PageRank矩阵和上次得到的PageRank矩阵不相同，则继续迭代，相同则不再迭代
        pageRank = tmpVk;
        System.out.println(Arrays.toString(pageRank));
    }
    System.out.println(Arrays.toString(pageRank));
}

5.4.2 测试结果

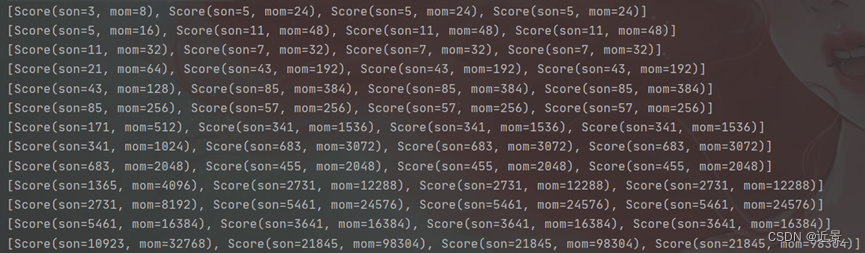
在这里插入图片描述
面对这个迭代结果，笔者还是有些许疑问的，书上最后的迭代结果说是趋于稳定了最后结果是[3/9，2/9，2/9，2/9]，可是本次实验最终并没有得到满意的结果，而是因为数据溢出直接终止了程序，但可以看到最后一次输出的结果已经很趋近于正确答案了，包括每次的迭代结果笔者也进行了笔算，也没发现什么问题。
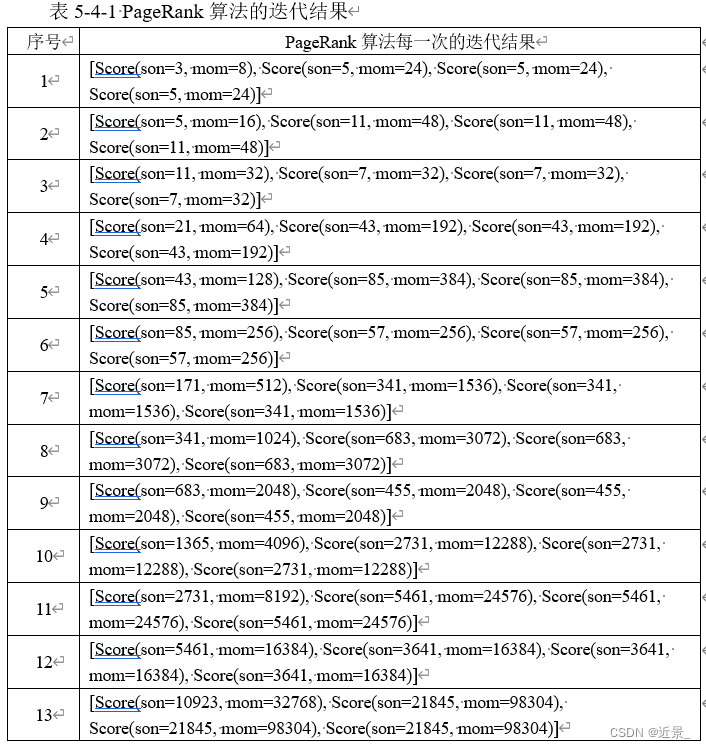
在这里插入图片描述
最后得到的结果也的确和书上答案[3/9，2/9，2/9，2/9]很接近了，笔者暂时没发现代码有什么问题，也许书上得出的答案也是经过粗略估计后选择了一个趋于稳定的值，后续若有新的发现则会及时更新报告。

五、小结与心得体会

本实验是用Java语言实现的，PageRank算法是笔者写的第二个实验，PageRank算法太熟悉了，当时考试前夕老师就说明了这是重中之重，在期末复习时也复习了很多遍这个算法，看到这个算法的实验感觉还是非常熟悉的，就着手去做了，PageRank算法的实现也相对来说比较简单，比较可以拿来说的就是这里定义了分数类Score，以及对矩阵的乘法的了解，分数类Score中也定义了涉及到分数加法和分数乘法的类静态方法，方便了算法的实现中直接调用。
在PageRank算法的实现过程中，笔者也是遇到了一些困难的，比如最终输出的结果并没有得到期望的[3/9，2/9，2/9，2/9]，笔者已经进行了多次验证，暂且未发现任何问题。
通过本实验，笔者对于Java面向对象的编程思想有了更进一步的认识，对于PageRank算法的思想也更为熟悉了。