LeetCode 297. Serialize and Deserialize Binary Tree【树,DFS,BFS,设计,二叉树,字符串】困难

本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

0 - 6 个月：字节跳动 3、Facebook 2、亚马逊 2、雅虎 Yahoo 2、特斯拉 2

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例 1：

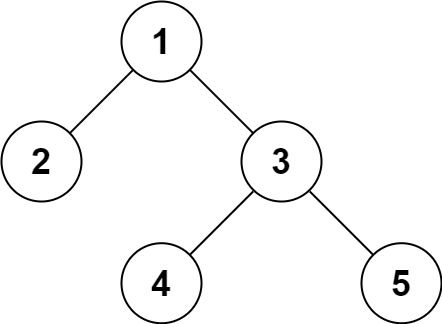
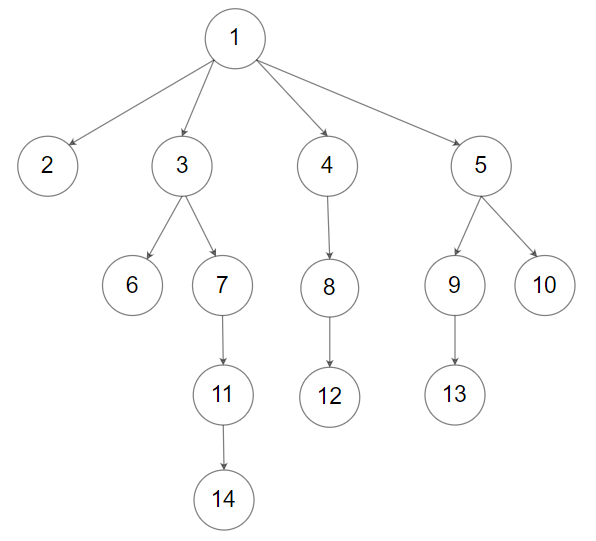
输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[1,2]

提示：

树中结点数在范围 [0, 10^4] 内
-1000 <= Node.val <= 1000

类似题目：

449. 序列化和反序列化二叉搜索树
297. 二叉树的序列化与反序列化困难
428. 序列化和反序列化 N 叉树困难

二叉树的序列化本质上是对其值进行编码，更重要的是对其结构进行编码。可以遍历树来完成上述任务。众所周知，我们一般有两个策略：广度优先搜索和深度优先搜索。

下面给出BFS和DFS做法。并借这道题稍微介绍一下拼接字符串的神器，`StringJoiner 类。 $St r in g J o in er$ 的两种主要用法：

StringJoiner sj = new StringJoiner(",", "[", "]"); 第一个参数表示拼接对象之间的连接符，第二个参数表示拼接后的前缀，第三个参数表示拼接后的后缀。例如将 sj.add("a"); sj.add("b") 之后sj.toString() 为 "[a,b]" 。
StringJoiner sj = new StringJoiner(","); 相比1，不指定前缀和后缀，上述例子拼接后为 "a,b" 。

解法1 广度优先搜索

最直接的做法是BFS。对于序列化，通过队列将结点数值依次拼成一个字符串。对当前出队结点 $h e a d$ ，考察其左右儿子，若有，则将数字转为字符串后拼接，若无，则拼接 null 。由于题目并不要求固定的格式，只要我们能从序列化后的字符串反序列化出树即可，因此序列化拼接形式是自由的。可以采用 StringBuilder 或 StringJoiner ，后者内部调用了 StringBuilder ，更便于格式化拼接。「代码」中使用 StringJoiner 完成拼接。

对于反序列化做法类似，也借助队列通过BFS方式完成。先将输入转为数组，利用 idx 跟踪当前反序列化的结点。首节点入队后，进入while循环，结点依次出队，idx 总是依次指向出队 head 结点的左右儿子，若 idx 指向的字符串不为 null ，则将其反序列化为结点，然后将 head 相应儿子指向它。这里用idx < n（ $n$ 是结点字符串数组的大小）来作为while的循环条件。

import java.util.StringJoiner;
public class Codec {
    public String serialize(TreeNode root) {
        if (root == null) return "";
        Queue<TreeNode> q = new ArrayDeque<>();
        StringJoiner sj = new StringJoiner(",");
        q.add(root);
        sj.add(Integer.toString(root.val));
        while (!q.isEmpty()) {
            TreeNode head = q.remove();
            if (head.left != null) {
                q.add(head.left);
                sj.add(Integer.toString(head.left.val));
            } else sj.add("null");
            if (head.right != null) {
                q.add(head.right);
                    sj.add(Integer.toString(head.right.val));
            } else sj.add("null");
        }
        return sj.toString();
    }
    public TreeNode deserialize(String data) {
        if (data.length() == 0) return null; // 特判：data == ""
        String[] nodes = data.split(",");
        Queue<TreeNode> q = new ArrayDeque<>();
        TreeNode root = new TreeNode(Integer.parseInt(nodes[0]));
        q.add(root);
        int idx = 1, n = nodes.length;
        while (idx < n) { // 不必以!q.isEmpty()作为判断条件
            TreeNode head = q.remove();
            if (!nodes[idx].equals("null")) {
                TreeNode left = new TreeNode(Integer.parseInt(nodes[idx])); 
                head.left = left; // left挂接到head
                q.add(left);
            } 
            idx++;
            if (!nodes[idx].equals("null")) {
                TreeNode right = new TreeNode(Integer.parseInt(nodes[idx])); 
                head.right = right; // right挂接到head
                q.add(right);
            } 
            idx++;
        }
        return root;
    }
}

解法2 深度优先搜索

广度优先搜索可以按照层次的顺序从上到下遍历所有的节点，深度优先搜索可以从一个根开始，一直延伸到某个叶，然后回到根，到达另一个分支。根据根节点、左节点和右节点之间的相对顺序，可以进一步将深度优先搜索策略区分为：

先序遍历
中序遍历
后序遍历

这里，我们选择先序遍历的编码方式，通过这样一个例子简单理解：

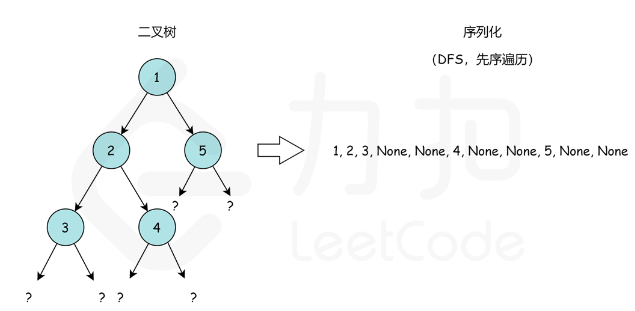
我们从根节点 $1$ 开始，序列化字符串是 $1,$ 。
然后我们跳到根节点 $2$ 的左子树，序列化字符串变成 $1, 2,$ 。现在从节点 $2$ 开始，我们访问它的左节点 $3$ （ $1, 2, 3, N o n e, N o n e,$ ）和右节点 $4 (1, 2, 3, N o n e, N o n e, 4, N o n e, N o n e)$ 。 $N o n e, N o n e,$ 是用来标记缺少左、右子节点，这就是我们在序列化期间保存树结构的方式。
最后，我们回到根节点 $1$ 并访问它的右子树，它恰好是叶节点 $5$ 。最后，序列化字符串是 $1, 2, 3, N o n e, N o n e, 4, N o n e, N o n e, 5, N o n e, N o n e,$ 。

即我们可以先序遍历这颗二叉树，遇到空子树的时候序列化成 $N o n e$ ，否则继续递归序列化。那么我们如何反序列化呢？首先我们需要根据 , 把原先的序列分割开来得到先序遍历的元素列表，然后从左向右遍历这个序列：

如果当前的元素为 $N o n e$ ，则当前为空树
否则先解析这棵树的左子树，再解析它的右子树

public class Codec {
    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        return serialize(root, new StringBuilder()).toString();
    }
    private StringBuilder serialize(TreeNode root, StringBuilder str) {
        if (root == null) str.append("None,");
        else {
            str.append(String.valueOf(root.val) + ",");
            str = serialize(root.left, str);
            str = serialize(root.right, str);
        }
        return str;
    }

    private Integer index;
    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String[] tokenArray = data.split(",");
        index = 0;
        return deserialize(tokenArray);
    }
    public TreeNode deserialize(String[] data) {
        if (data[index].equals("None")) {
            ++index;
            return null;
        }
        TreeNode root = new TreeNode(Integer.valueOf(data[index]));
        ++index;
        root.left = deserialize(data);
        root.right = deserialize(data);
        return root;
    }
}

复杂度分析：

时间复杂度：在序列化和反序列化函数中，我们只访问每个节点一次，因此时间复杂度为 $O (n)$ ，其中 $n$ 是节点数，即树的大小。
空间复杂度：在序列化和反序列化函数中，我们递归会使用栈空间，故渐进空间复杂度为 $O (n)$ 。

解法3 括号表示编码 + 递归下降解码

我们也可以这样表示一颗二叉树：

如果当前的树为空，则表示为 $X$
如果当前的树不为空，则表示为 (<LEFT_SUB_TREE>)CUR_NUM(RIGHT_SUB_TREE) ，其中：
1. <LEFT_SUB_TREE> 是左子树序列化之后的结果
2. <RIGHT_SUB_TREE> 是右子树序列化之后的结果
3. CUR_NUM 是当前节点的值

根据这样的定义，我们很好写出序列化的过程，后序遍历这颗二叉树即可，那如何反序列化呢？根据定义，我们可以推导出这样的巴科斯范式（BNF）：
$(T)\ |\ X$
它的意义是：用 $T$ 代表一棵树序列化之后的结果， $∣$ 表示 $T$ 的构成为 $(T) n u m (T)$ 或者 $X$ ， $∣$ 左边是对 $T$ 的递归定义，右边规定了递归终止的边界条件。

因为：

$T$ 的定义中，序列中的第一个字符要么是 $X$ ，要么是 $($ ，所以这个定义是不含左递归的
当我们开始解析一个字符串的时候，如果开头是 $X$ ，我们就知道这一定是解析一个「空树」的结构，
如果开头是 ( ，我们就知道需要解析 $(T) n u m (T)$ 的结构，
因此这里两种开头和两种解析方法一一对应，可以确定这是一个无二义性的文法

我们只需要通过开头的第一个字母是 $X$ 还是 $($ 来判断使用哪一种解析方法。所以这个文法是 $LL (1)$ 型文法，如果你不知道什么是 $LL (1)$ 型文法也没有关系，只需要知道它定义了一种递归的方法来反序列化，也保证了这个方法的正确性——我们可以设计一个递归函数：

这个递归函数传入两个参数，带解析的字符串和当前当解析的位置 $pt r$ ， $pt r$ 之前的位置是已经解析的， $pt r$ 和 $pt r$ 后面的字符串是待解析的
如果当前位置为 $X$ 说明解析到了一棵空树，直接返回
否则当前位置一定是 $($ ，对括号内部按照 $(T) n u m (T)$ 的模式解析

具体请参考下面的代码。

public class Codec {
    public String serialize(TreeNode root) {
        if (root == null) return "X";
        String left = "(" + serialize(root.left) + ")";
        String right = "(" + serialize(root.right) + ")";
        return left + root.val + right;
    }
    private int ptr;
    public TreeNode deserialize(String data) {
        ptr = 0;
        return parse(data);
    }
    public TreeNode parse(String data) {
        if (data.charAt(ptr) == 'X') {
            ++ptr;
            return null;
        }
        TreeNode cur = new TreeNode(0);
        cur.left = parseSubtree(data);
        cur.val = parseInt(data);
        cur.right = parseSubtree(data);
        return cur;
    }
    public TreeNode parseSubtree(String data) {
        ++ptr; // 跳过左括号
        TreeNode subtree = parse(data);
        ++ptr; // 跳过右括号
        return subtree;
    }
    public int parseInt(String data) {
        int x = 0, sgn = 1;
        if (!Character.isDigit(data.charAt(ptr))) {
            sgn = -1;
            ++ptr;
        }
        while (Character.isDigit(data.charAt(ptr))) 
            x = x * 10 + data.charAt(ptr++) - '0';
        return x * sgn;
    }
}

复杂度分析：

时间复杂度：序列化时做了一次遍历，渐进时间复杂度为 $O (n)$ 。反序列化时，在解析字符串的时候 $pt r$ 指针对字符串做了一次顺序遍历，字符串长度为 $O (n)$ ，故这里的渐进时间复杂度为 $O (n)$ 。
空间复杂度：考虑递归使用的栈空间的大小，这里栈空间的使用和递归深度有关，递归深度又和二叉树的深度有关，在最差情况下，二叉树退化成一条链，故这里的渐进空间复杂度为 $O (n)$ 。