---

区间DP

石子合并

题目描述：
设有 $N$ 堆石子排成一排，其编号为 $1,2,3,\dots ,N$。

每堆石子有一定的质量，可以用一个整数来描述，现在要将这 $N$ 堆石子合并成为一堆。

每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。

例如有 $4$ 堆石子分别为 1 3 5 2， 我们可以先合并 $1、2$ 堆，代价为 $4$，得到 4 5 2， 又合并 $1$、$2$ 堆，代价为 $9$，得到 9 2，再合并得到 $11$，总代价为 $4+9+11=24$；

如果第二步是先合并 $2$、$3$ 堆，则代价为 $7$，得到 4 7，最后一次合并代价为 $11$，总代价为 $4+7+11=22$。

问题是：找出一种合理的方法，使总的代价最小，输出最小代价。

输入格式：
第一行一个数 $N$ 表示石子的堆数 $N$。

第二行 $N$ 个数，表示每堆石子的质量(均不超过 $1000$)。

输出格式：
输出一个整数，表示最小代价。

数据范围：
$1\le N\le 300$

输入样例：

4
1 3 5 2

输出样例：

22

分析思路

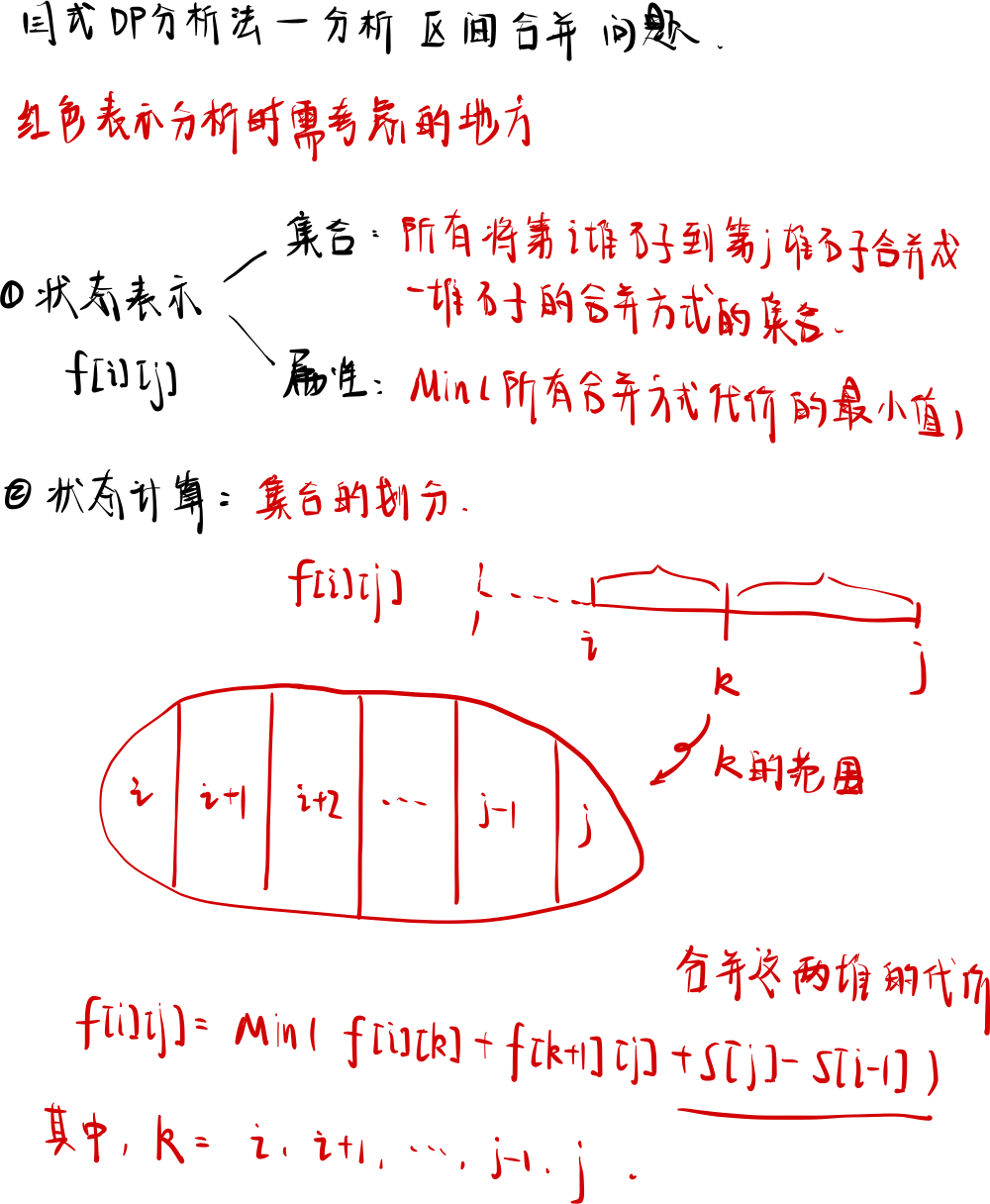
代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 310;
int f[N][N], s[N];

int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; ++i)
	{
		cin >> s[i];
		s[i] = s[i] + s[i - 1]; // 化为前缀和数组
	}
	for (int len = 2; len <= n; ++len)
	{
		for (int i = 1; i + len - 1 <= n; ++i)
		{
			int l = i, r = i + len - 1;
			f[l][r] = 0x3f3f3f3f;
			for (int k = l; k < r; ++k)
				f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
		}
	}
	cout << f[1][n] << endl;
	return 0;
}

计数类DP

整数划分

题目描述：
一个正整数 $n$ 可以表示成若干个正整数之和，形如：$n=n_1+n_2+\dots +n_k$，其中 $n_1\ge n_2\ge \dots \ge n_k,k\ge 1$。

我们将这样的一种表示称为正整数 $n$ 的一种划分。

现在给定一个正整数 $n$，请你求出 $n$ 共有多少种不同的划分方法。

输入格式：
共一行，包含一个整数 $n$。

输出格式：
共一行，包含一个整数，表示总划分数量。

由于答案可能很大，输出结果请对 $10^9+7$ 取模。

数据范围：
$1\le n\le 1000$

输入样例：

5

输出样例：

7

完全背包DP的解法

二维数组实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1010, mod = 1e9 + 7;
int f[N][N];

int main()
{
	int n;
	cin >> n;
	for (int i = 0; i <= n; ++i) f[i][0] = 1;
	for (int i = 1; i <= n; ++i)
		for (int j = 0; j <= n; ++j)
		{
			f[i][j] = f[i - 1][j]; // 一个i都不放的情况
			if (j >= i) f[i][j] = f[i - 1][j] + f[i][j - i];
		}
	cout << f[n][n] << endl;
	return 0;
}

一维优化实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1010, mod = 1e9 + 7;
int f[N];

int main()
{
	int n;
	cin >> n;
	f[0] = 1;

	for (int i = 1; i <= n; ++i)
		for (int j = i; j <= n; ++j)
			f[j] = (f[j] + f[j - i]) % mod;
	cout << f[n] << endl;
	return 0;
}

另类DP状态表示的解法（分拆数）

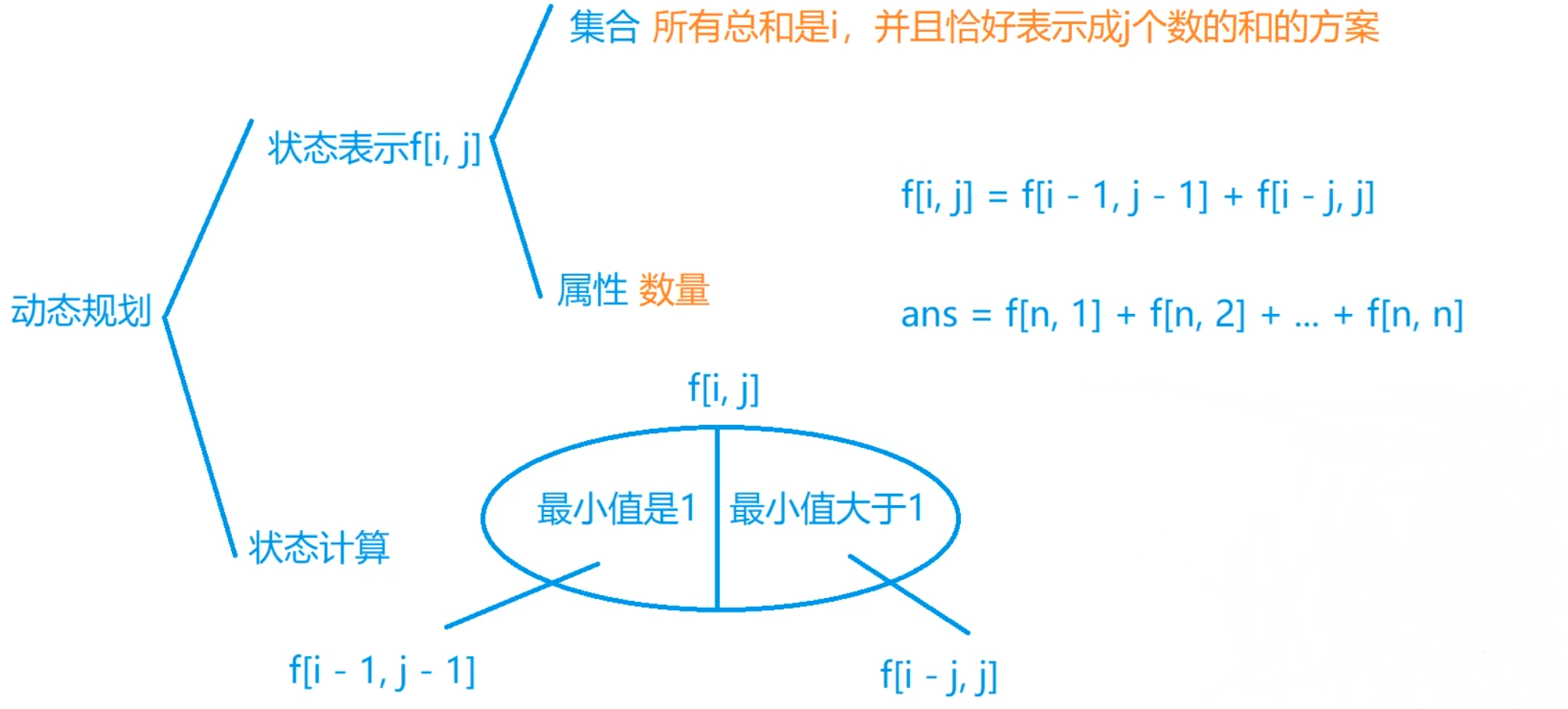
状态表示：
f[i][j] 表示总和为 $i$，总个数为 $j$ 的方案数。

状态转移方程：
f[i][j] = f[i - 1][j - 1] + f[i - j][j];

二维数组实现

const int N = 1010, mod = 1e9 + 7;
int f[N][N];

int main()
{
	int n;
	cin >> n;
	f[0][0] = 1;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= i; ++j)
			(f[i][j] = f[i - 1][j - 1] + f[i - j][j]) % mod;
	int res = 0;
	for (int i = 1; i <= n; ++i) res = (res + f[n][i]) % mod;
	cout << res << endl;
	return 0;
}

一维优化实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1010, mod = 1e9 + 7;
int f[N][N];

int main()
{
	int n;
	cin >> n;
	f[0][0] = 1;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= i; ++j)
			(f[i][j] = f[i - 1][j - 1] + f[i - j][j]) % mod;
	int res = 0;
	for (int i = 1; i <= n; ++i) res = (res + f[n][i]) % mod;
	cout << res << endl;
	return 0;
}

数位统计DP

计数问题

题目描述：
给定两个整数 $a$ 和 $b$，求 a 和 b 之间的所有数字中 $0$∼$9$ 的出现次数。

例如，$a=1024$，$b=1032$，则 $a$ 和 $b$ 之间共有 $9$ 个数如下：

1024 1025 1026 1027 1028 1029 1030 1031 1032

其中 $0$ 出现 $10$ 次，$1$ 出现 $10$ 次，$2$ 出现 $7$ 次，$3$ 出现 $3$ 次等等…

输入格式：
输入包含多组测试数据。

每组测试数据占一行，包含两个整数 $a$ 和 $b$。

当读入一行为 0 0 时，表示输入终止，且该行不作处理。

输出格式：
每组数据输出一个结果，每个结果占一行。

每个结果包含十个用空格隔开的数字，第一个数字表示 $0$ 出现的次数，第二个数字表示 $1$ 出现的次数，以此类推。

数据范围：
$0<a,b<10^8$

输入样例：

1 10
44 497
346 542
1199 1748
1496 1403
1004 503
1714 190
1317 854
1976 494
1001 1960
0 0

输出样例：

1 2 1 1 1 1 1 1 1 1
85 185 185 185 190 96 96 96 95 93
40 40 40 93 136 82 40 40 40 40
115 666 215 215 214 205 205 154 105 106
16 113 19 20 114 20 20 19 19 16
107 105 100 101 101 197 200 200 200 200
413 1133 503 503 503 502 502 417 402 412
196 512 186 104 87 93 97 97 142 196
398 1375 398 398 405 499 499 495 488 471
294 1256 296 296 296 296 287 286 286 247

注意

讨论数字0出现次数时，要注意避免前导0的出现。

例如：
讨论1234中第3位的0的出现次数时，不可以让第一二位的数字取0，这样就会变成 04 出现了前导0。故此时前两位只能取 1 ~ 12 之间的数字。

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
using namespace std;

/*

001~abc-1, 999

abc
    1. num[i] < x, 0
    2. num[i] == x, 0~efg
    3. num[i] > x, 0~999

*/

// 获取num中以l开头，r结尾组成的数是多少，就是求思路中的“abc”
int get(vector<int> num, int l, int r)
{
    int res = 0;
    for (int i = l; i >= r; i -- ) res = res * 10 + num[i];
    return res;
}

// 求10的x次方
int power10(int x)
{
    int res = 1;
    while (x -- ) res *= 10;
    return res;
}

// count函数用于计数 1 ~ n 中，x出现的次数
int count(int n, int x)
{
    if (!n) return 0; // 如果n为0，返回0；因为我们统计的是从1~n中每个数出现的次数（注意数据范围取不到0的）

    // num数组用于存储每一位上的数是多少（注意是倒着的，因此在下面for循环时，也是倒着遍历的）
    vector<int> num; 
    // 如 n = 12345
    // 则 num = {5,4,3,2,1}
    while (n)
    {
        num.push_back(n % 10);
        n /= 10;
    }
    // n此时表示原来n有多少位，然后用于计算i在每一位上的数有多少个
    n = num.size();
    
    // 计算i在每一位上的数有多少个
    int res = 0;
    // - !x的作用是，当x = 0时，要统计0在每一位上的数的个数，因为0不能在首位，所以此时 - !x = -1 ，即从第二位开始枚举
    for (int i = n - 1 - !x; i >= 0; i -- )
    {
        // ---------------------------第 ① 种情况---------------------------
        if (i < n - 1) // 枚举到最高位时，第①种情况是不存在的，因此需要i < n - 1特判一下
        {
            res += get(num, n - 1, i + 1) * power10(i); 
            if (!x) res -= power10(i); // 如果 x == 0,要减去在首位的计数
        }
        // ---------------------------第 ② 种情况---------------------------
        // ② 中 第 Ⅰ 种情况，为0，不用写
        if (num[i] == x) res += get(num, i - 1, 0) + 1; // 即 ② 中的第 Ⅱ 种情况 (d = x)
        else if (num[i] > x) res += power10(i); // 即 ② 中的第 Ⅲ 种情况  （d > x）
    }

    return res;
}

int main()
{
    int a, b;
    while (cin >> a >> b , a || b)
    {
        if (a > b) swap(a, b); // 保证 b 是始终大于 a 的（因为题目中输入的第一个数 a 有可能大于第二个数 b ）

        // 计算的是b和a中i出现的次数
        // 要求的是b到a之间的数的数，因此采用前缀和的思想，用b的计数-a的计数
        for (int i = 0; i <= 9; i ++ )
            cout << count(b, i) - count(a - 1, i) << ' ';
        cout << endl;
    }

    return 0;
}

状态压缩DP

蒙德里安的梦想

题目描述：
求把 $N\times M$ 的棋盘分割成若干个 $1\times 2$ 的长方形，有多少种方案。

例如当 $N=2$，$M=4$ 时，共有 $5$ 种方案。当 $N=2$，$M=3$ 时，共有 $3$ 种方案。

如下图所示：

输入格式：
输入包含多组测试用例。

每组测试用例占一行，包含两个整数 $N$ 和 $M$。

当输入用例 $N=0$，$M=0$ 时，表示输入终止，且该用例无需处理。

输出格式：
每个测试用例输出一个结果，每个结果占一行。

数据范围：
$1\le N,M\le 11$

输入样例：

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

输出样例：

1
0
1
2
3
5
144
51205

实现思路

$f[i][j]$ 中用 $i$ 表示前 $i$ 列，$j$ 的二进制形式用来表示当前横块的选取情况。

例如：

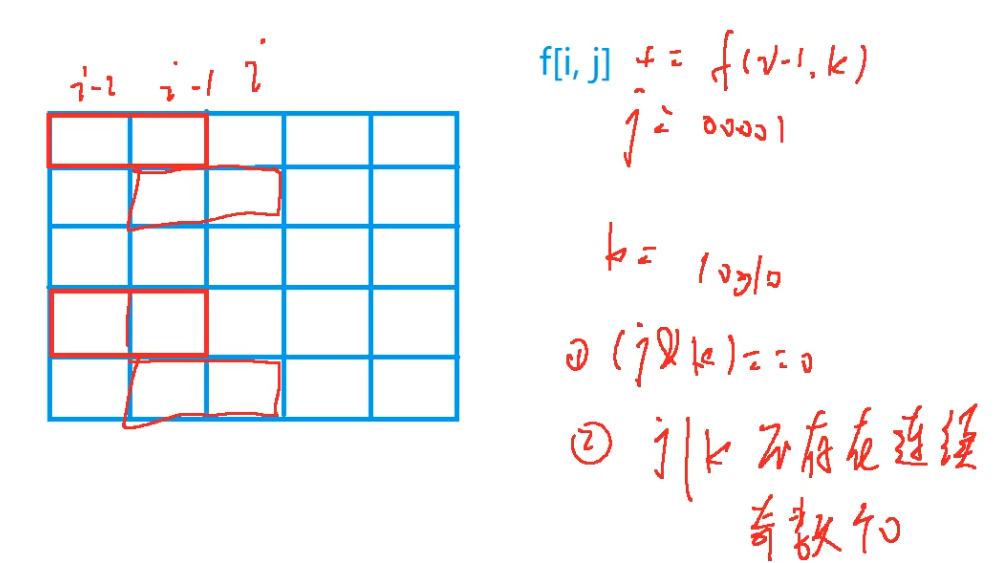
图中的第 $i$ 列的横块的选取情况 $j$ 为 $01001$，第 $i-1$ 列的横块选取情况
$k$ 为 $10010$。

为了避免竖块无法插入到空隙中，我们必须要让选取情况中不出现奇数个0。同时注意不能让前后列中的横块前后部分重合。

若 $k、j$ 分别为 $i-1$ 和 $i$ 列的选取情况，则需要满足：

• $k$ & $j$ $==0$
• $k$ | $j$ 不存连续的奇数个0

通过以上可以得到状态转移方程：

f[i][j] += f[i - 1][k];

朴素实现

#include <cstring>
#include <iostream>

using namespace std;

const int N = 12, M = 1 << N;

int n, m;
long long f[N][M];
bool st[M];

int main()
{
    while (cin >> n >> m, n || m)
    {
        for (int i = 0; i < 1 << n; i ++ ) // 模拟各种状态是否存在连续奇数个0
        {
            int cnt = 0; // 用于判断奇数个0
            st[i] = true;
            for (int j = 0; j < n; j ++ ) // 对压缩的二进制状态进行提取
                if (i >> j & 1)
                {
                    if (cnt & 1) st[i] = false;
                    cnt = 0;
                }
                else cnt ++ ;
            if (cnt & 1) st[i] = false;
        }

        memset(f, 0, sizeof f);
        f[0][0] = 1;
        for (int i = 1; i <= m; i ++ )
            for (int j = 0; j < 1 << n; j ++ )
                for (int k = 0; k < 1 << n; k ++ )
                    if ((j & k) == 0 && st[j | k])
                        f[i][j] += f[i - 1][k];

        cout << f[m][0] << endl;
    }
    return 0;
}

注意：
令 $f[0][0]=1$，由于每一列的摆放都是由前一列决定的，第一列要模拟出各种摆放情况，让第二列的摆放因而可以变成各个情况，但实际上第一列没有摆放任何横块，而 $f[0][0]=1$ 让第一列的各种模拟摆放情况都有个最基础的方案数 1。

预处理优化实现

const int N = 12, M = 1 << N;
int f[N][M];
bool valid[M];
vector<int> state[M];

int main()
{
	int n, m;
	while (cin >> n >> m, n || m)
	{
		for (int i = 0; i < 1 << n; ++i)
		{
			int cnt = 0;
			bool is_valid = true;
			for (int j = 0; j < n; ++j)
			{
				if (i >> j & 1)
				{
					if (cnt & 1)
					{
						is_valid = false;
						break;
					}
					cnt = 0;
				}
				else cnt++;
			}
			if (cnt & 1) is_valid = false;
			valid[i] = is_valid;
		}

		 // 提前在 O(n^2) 情况下，将有效状态都预处理出来
		 // 避免在 O(n^3) 情况下，才开始遍历所有状态中的有效状态
		for (int i = 0; i < 1 << n; ++i)
		{
			state[i].clear();
			for (int j = 0; j < 1 << n; ++j)
				if ((i & j) == 0 && valid[i | j]) state[i].push_back(j);
		}
		memset(f, 0, sizeof f);
		f[0][0] = 1;
		for (int i = 1; i <= m; ++i)
		{
			for (int j = 0; j < 1 << n; ++j)
				for (auto e : state[j])
					f[i][j] += f[i - 1][e];
		}
		cout << f[m][0] << endl;
	}
	return 0;
}

最短Hamilton路径

题目描述：
给定一张 $n$ 个点的 带权无向图，点从 $0\sim n-1$ 标号，求起点 $0$ 到终点 $n-1$ 的最短 Hamilton 路径。

Hamilton 路径的定义是从 $0$ 到 $n-1$ 不重不漏地经过每个点恰好一次。

输入格式：
第一行输入整数 $n$。

接下来 $n$ 行每行 $n$ 个整数，其中第 $i$ 行第 $j$ 个整数表示点 $i$ 到 $j$ 的距离（记为 $a[i,j]$）。

对于任意的 $x,y,z$，数据保证 $a[x,x]=0$，$a[x,y]=a[y,x]$，并且 $a[x,y]+a[y,z]\ge a[x,z]$。

输出格式：
输出一个整数，表示最短 Hamilton 路径的长度。

数据范围：
$1\le n\le 20$

$0\le a[i,j]\le 107$

输入样例：

5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0

输出样例：

18

实现思路

采用二进制数来表示各个点位的选取状态。

状态分析：

可以得到状态转移方程：

f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 20, M = 1 << N;
int w[N][N], f[M][N];

int main()
{
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i)
		for (int j = 0; j < n; ++j) cin >> w[i][j];
	
	memset(f, 0x3f, sizeof f);
	f[1][0] = 0;
	// 因为起点为0号点，所以初始条件直接设为 1
	// 因为0号点为必须经过的点，所以+=2每回从第二位开始更新
	for (int i = 1; i < 1 << n; i += 2)
	{
		for (int j = 0; j < n; ++j) // 枚举每个节点为阶段性终点
		{
			if (!(i >> j & 1)) continue;
			for (int k = 0; k < n; ++k) // 枚举每个节点为中间节点
				if ((i - (1 << j)) >> k & 1)
					f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
		}
	}
	cout << f[(1 << n) - 1][n - 1] << endl;
	return 0;
}

树形DP

大盗阿福

题目描述：
阿福是一名经验丰富的大盗。趁着月黑风高，阿福打算今晚洗劫一条街上的店铺。

这条街上一共有 $N$ 家店铺，每家店中都有一些现金。

阿福事先调查得知，只有当他同时洗劫了两家相邻的店铺时，街上的报警系统才会启动，然后警察就会蜂拥而至。

作为一向谨慎作案的大盗，阿福不愿意冒着被警察追捕的风险行窃。

他想知道，在不惊动警察的情况下，他今晚最多可以得到多少现金？

输入格式：
输入的第一行是一个整数 $T$，表示一共有 $T$ 组数据。

接下来的每组数据，第一行是一个整数 $N$，表示一共有 $N$ 家店铺。

第二行是 $N$ 个被空格分开的正整数，表示每一家店铺中的现金数量。

每家店铺中的现金数量均不超过 $1000$。

输出格式：
对于每组数据，输出一行。

该行包含一个整数，表示阿福在不惊动警察的情况下可以得到的现金数量。

数据范围：
$1\le T\le 50,1\le N\le 10^5$

输入样例：

2
3
1 8 2
4
10 7 6 14

输出样例：

8
24

状态机解法

将状态数组定为二维，即 $f[i][j]$。

数组的第一维表示抢劫前 $i$ 家能得到的最多现金数量。

数组的第二维储存两种情况：偷与不偷。

• $f[i][0]$ 代表的是不偷第 $i$ 家店铺能得到的最多现金数量；

• $f[i][1]$ 代表的是偷第i家店铺能得到的最多现金数量。

// 状态转移方程
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + w[i];

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1e5 + 10;
int f[N][2], w[N];

int main()
{
	int T;
	cin >> T;
	while (T--)
	{
		int n;
		cin >> n;
		memset(f, 0, sizeof f);

		for (int i = 1; i <= n; ++i) cin >> w[i];
		f[1][0] = 0, f[1][1] = w[1];
		for (int i = 2; i <= n; ++i)
		{
			f[i][0] = max(f[i - 1][0], f[i - 1][1]);
			f[i][1] = f[i - 1][0] + w[i];
		}
		cout << max(f[n][0], f[n][1]) << endl;
	}
	return 0;
}

扩展：线性DP实现

$f[i]$ 表示抢劫前 $i$ 家能得到的最多现金数量。

$f[i]$分为两种情况：

• 不抢第 $i$ 家 $f[i]=f[i-1]$
• 抢劫第 $i$ 家 $f[i]=f[i-2]+w[i]$

// 状态转移方程
f[i] = max(f[i - 1], f[i - 2] + w[i])

注意初始状态：

1. $f[0]=0$
2. $f[1]=w[1]$

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1e5 + 10;
int f[N], w[N];

int main()
{
	int T;
	cin >> T;
	while (T--)
	{
		int n;
		cin >> n;	
		for (int i = 1; i <= n; ++i) cin >> w[i];
		memset(f, 0, sizeof f);
		f[0] = 0;
		f[1] = w[1];
		for (int i = 2; i <= n; ++i) 
			f[i] = max(f[i - 1], f[i - 2] + w[i]);
		cout << f[n] << endl;
	}
	return 0;
}

没有上司的舞会

题目描述：
Ural 大学有 $N$ 名职员，编号为 $1$ ~ $N$。

他们的关系就像一棵以校长为根的树，父节点就是子节点的直接上司。

每个职员有一个快乐指数，用整数 $H_i$ 给出，其中 $1\le i\le N$。

现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。

在满足这个条件的前提下，主办方希望激请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。

输入格式：

第一行一个整数 $N$。

接下来 $N$ 行，第 $i$ 行表示号职员的快乐指数 $H_i$。

接下来 $N-1$ 行，每行输入一对整数 $L,K$，表示 $K$ 是 $L$ 的直接上司输出格式。

输出格式：
输出最大的快乐指数。

数据范围：
$1\le N\le 6000$
$-128\le H_i\le 127$

输入样例：

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5

输出样例：

5

思路

状态表示：

$f[u][1]$ 表示以 $u$ 为根节点的子树并且包括 $u$ 的总快乐指数。

$f[u][0]$ 表示以 $u$ 为根节点并且不包括 $u$ 的总快乐指数。

状态计算：

要想求得一棵以 $u$ 为根节点的子树的最大指数分为两种：

• 选 $u$ 节点
• 不选 $u$ 节点

记点 $u$ 的子节点是 $j$

1. 选 $u$，$f[u][1]=\sum f[j][0]$。
2. 不选 $u$，$f[u][0]=\sum max(f[j][1],f[j][0])$ 记根节点为 root。

从 root 开始 dfs 一遍即可最后输出 $max(f[root][1],f[root][0])$

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 6010;
int f[N][2], w[N], n;
int h[N], e[N], ne[N], idx;
bool has_fa[N];

void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
void dfs(int u)
{
	f[u][1] = w[u];
	for (int i = h[u]; i != -1; i = ne[i])
	{
		int j = e[i];
		dfs(j);
		f[u][1] += f[j][0];
		f[u][0] += max(f[j][0], f[j][1]);
	}
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; ++i) cin >> w[i];
	memset(h, -1, sizeof f);
	for (int i = 1; i < n; ++i)
	{
		int a, b;
		cin >> a >> b;
		add(b, a);
		has_fa[a] = true;
	}
	int root = 1;
	while (has_fa[root]) root++; // 找到父节点
	dfs(root);
	cout << max(f[root][1], f[root][0]) << endl;
	return 0;
}

战略游戏

题目描述：
鲍勃喜欢玩电脑游戏，特别是战略游戏，但有时他找不到解决问题的方法，这让他很伤心。

现在他有以下问题。

他必须保护一座中世纪城市，这条城市的道路构成了一棵树。

每个节点上的士兵可以观察到所有和这个点相连的边。

他必须在节点上 放置最少数量的士兵，以便他们可以观察到所有的边。

你能帮助他吗？

例如，下面的树：

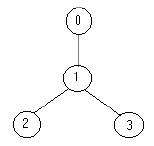
只需要放置 $1$ 名士兵（在节点 $1$ 处），就可观察到所有的边。

输入格式：
输入包含多组测试数据，每组测试数据用以描述一棵树。

对于每组测试数据，第一行包含整数 $N$，表示树的节点数目。

接下来 $N$ 行，每行按如下方法描述一个节点。

节点编号：(子节点数目) 子节点 子节点 …

节点编号从 $0$ 到 $N-1$，每个节点的子节点数量均不超过 $10$，每个边在输入数据中只出现一次。

输出格式：
对于每组测试数据，输出一个占据一行的结果，表示最少需要的士兵数。

数据范围：
$0<N\le 1500$

一个测试点所有 $N$ 相加之和不超过 $300650$。

输入样例：

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

输出样例：

1
2

思路

状态表示：

$f[u][0]$：所有以 $u$ 为根的子树中选择，并且不选 $u$ 这个点的方案。

$f[u][1]$：所有以 $u$ 为根的子树中选择，并且选 $u$ 这个点的方案。

属性：$Min$

状态计算：

• 当前 $u$ 结点不选，子结点一定选 $f[u][0]=\sum (f[soni][1])$。

• 当前 $u$ 结点选，子结点可选可不选 $f[u][1]=\sum min(f[soni][0],f[soni][1])$。

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 1510;
int h[N], e[N], ne[N], idx;
int f[N][2], n;
bool has_fa[N];


void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
void dfs(int u)
{
	f[u][1] = 1;
	for (int i = h[u]; ~i; i = ne[i])
	{
		int j = e[i];
		dfs(j);
		f[u][0] += f[j][1];
		f[u][1] += min(f[j][0], f[j][1]);
	}
}
int main()
{
	while (cin >> n)
	{
		memset(h, -1, sizeof h), idx = 0;
		memset(has_fa, 0, sizeof has_fa);
		memset(f, 0, sizeof f);
		for (int i = 0; i < n; ++i)
		{
			int T, a, b;
			scanf("%d:(%d)", &a, &T);
			while (T--)
			{
				cin >> b;
				add(a, b);
				has_fa[b] = true;
			}
		}
		int root = 0;
		while (has_fa[root]) root++;
		dfs(root);
		cout << min(f[root][1], f[root][0]) << endl;
	}
	return 0;
}

记忆化搜索

滑雪

题目描述：
给定一个 $R$ 行 $C$ 列的矩阵，表示一个矩形网格滑雪场。

矩阵中第 $i$ 行第 $j$ 列的点表示滑雪场的第 $i$ 行第 $j$ 列区域的高度。

一个人从滑雪场中的某个区域内出发，每次可以向上下左右任意一个方向滑动一个单位距离。

当然，一个人能够滑动到某相邻区域的前提是该区域的高度低于自己目前所在区域的高度。

下面给出一个矩阵作为例子：

 1  2  3  4 5

16 17 18 19 6

15 24 25 20 7

14 23 22 21 8

13 12 11 10 9

在给定矩阵中，一条可行的滑行轨迹为 24−17−2−1。

在给定矩阵中，最长的滑行轨迹为 25−24−23−…−3−2−1，沿途共经过 $25$ 个区域。

现在给定你一个二维矩阵表示滑雪场各区域的高度，请你 找出在该滑雪场中能够完成的最长滑雪轨迹，并输出其长度(可经过最大区域数)。

输入格式：
第一行包含两个整数 $R$ 和 $C$。

接下来 $R$ 行，每行包含 $C$ 个整数，表示完整的二维矩阵。

输出格式：
输出一个整数，表示可完成的最长滑雪长度。

数据范围：
$1\le R,C\le 300$
$0\le$矩阵中整数$\le 10000$

输入样例：

5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9

输出样例：

25

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 310;
int f[N][N], g[N][N];
int n, m, dx[4]{ -1, 0, 1, 0 }, dy[4]{0, -1, 0, 1};

int dfs(int x, int y)
{
	if (~f[x][y]) return f[x][y];
	f[x][y] = 1; // 最小也是一步
	for (int i = 0; i < 4; ++i)
	{
		int tx = x + dx[i], ty = y + dy[i];
		if (tx < 1 || tx > n || ty < 1 || ty > m) continue;
		if (g[x][y] > g[tx][ty])
			f[x][y] = max(f[x][y], dfs(tx, ty) + 1);
	}
	return f[x][y];
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= n; ++j) cin >> g[i][j];
	
	memset(f, -1, sizeof f);

	int res = 0;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
			res = max(res, dfs(i, j));

	cout << res << endl;

	return 0;
}