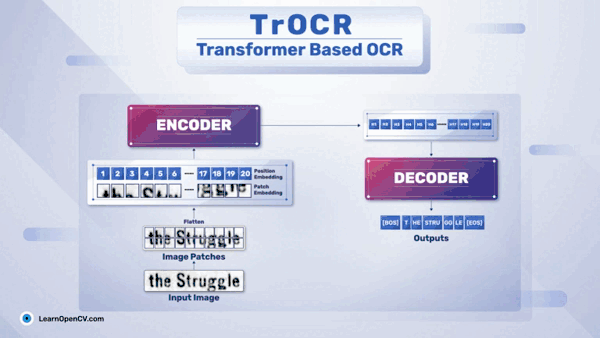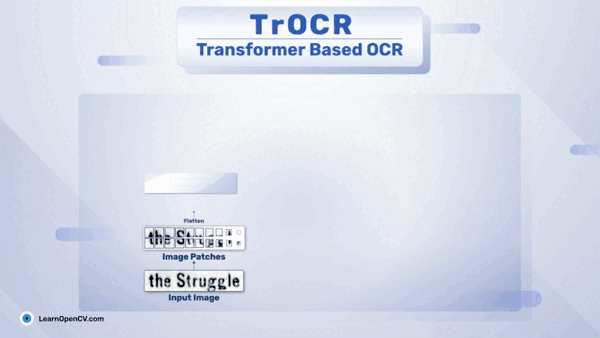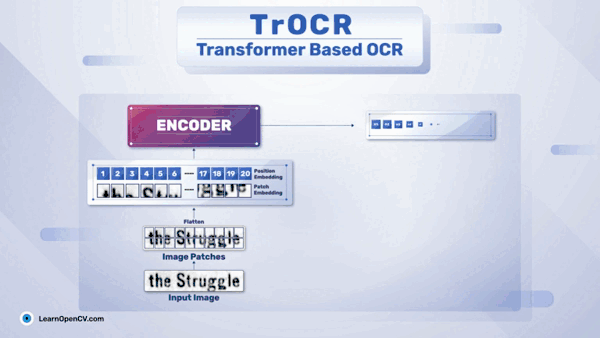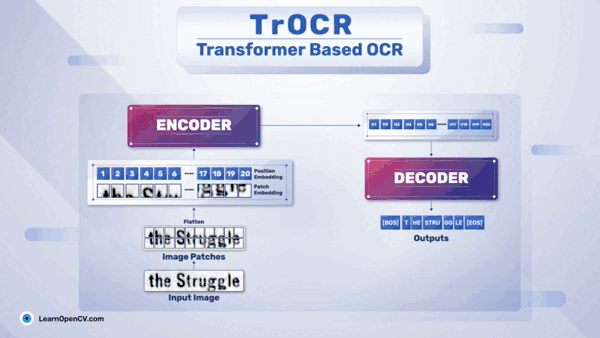
1、访问器模式的提出
在软件开发过程中,早已发布的软件版本,由于需求的变化,需要给某个类层次结构增加新的方法。如果在该基类和子类中都添加新的行为方法,将给代码原有的结构带来破坏,同时,也违反了修改封闭,扩展开放的原则。访问器模式可以实现不改变原有代码结构的前提下,基于双向分发机制(2次虚函数绑定实例对象),通过扩展的方法实现新的接口。
2、需求描述
有2个固定数量的元素AB,每个元素有不同方法。A、B元素的方法有可能还会更新。请设计一个功能代码,可以应对方法更新的代码。
3、功能实现
(1)UML图如下:
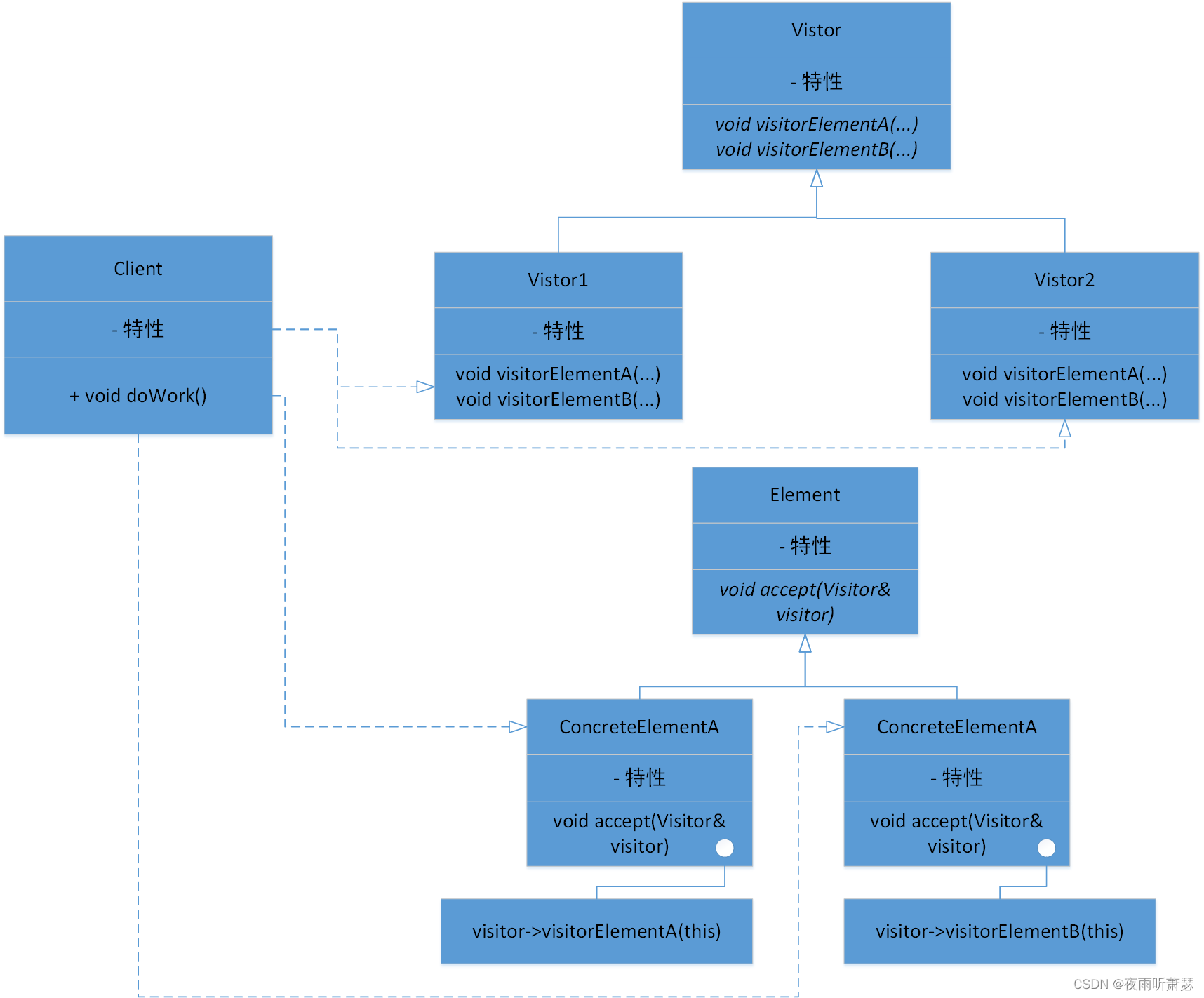
(2)代码实现如下:
#include <iostream>
class ConcreteElementA;
class ConcreteElementB;
class Visitor
{
public:
virtual void visitorElementA(ConcreteElementA& element)=0; //第二次虚函数
virtual void visitorElementB(ConcreteElementB& element)=0;
};
class Element
{
public:
virtual void accept(Visitor& visitor)=0; //第一次虚函数
virtual ~Element(){};
};
class ConcreteElementA:public Element
{
public:
void accept(Visitor &visitor) override
{
visitor.visitorElementA(*this);
}
};
class ConcreteElementB:public Element
{
public:
void accept(Visitor &visitor) override
{
visitor.visitorElementB(*this);
}
};
// 上面是稳定的代码结构
// 下面是扩展应对方法改变的功能类
class ConcreteVisitor1:public Visitor
{
public:
void visitorElementA(ConcreteElementA &element) override
{
std::cout << "Visitor1 process visitorElementA "<< &element << std::endl;
}
void visitorElementB(ConcreteElementB &element) override
{
std::cout << "Visitor1 process visitorElementB " << &element << std::endl;
}
};
class ConcreteVisitor2:public Visitor
{
public:
void visitorElementA(ConcreteElementA &element) override
{
std::cout << "Visitor2 process visitorElementA " << &element<< std::endl;
}
void visitorElementB(ConcreteElementB &element) override
{
std::cout << "Visitor2 process visitorElementB " << &element << std::endl;
}
};
class Client{
public:
void doWork()
{
ConcreteVisitor1 visitor1;
ConcreteElementA element1A;
element1A.accept(visitor1);
ConcreteElementB element1B;
element1B.accept(visitor1);
ConcreteVisitor2 visitor2;
ConcreteElementA element2A;
element2A.accept(visitor2);
ConcreteElementB element2B;
element2B.accept(visitor2);
}
};
int main()
{
Client obj;
obj.doWork();
return 0;
}
程序运行的结果如下:
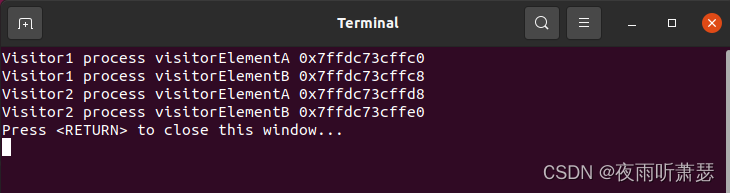
上面的代码,ConcreteElementA和ConcreteElementB的方法更新,通过Visitor基类的扩展子类来实现。
通过上面的代码可以看出,使用访问器模式的应用场景必须满足下面的条件:
(1)Element的子类个数必须确定。
(2)Visitor的子类必须实现Element的所有子类方法。