空间中的平面和直线
知识点1 平面方程
1.平面的法向量与法式
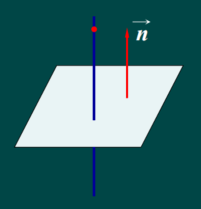
定义1 若向量n 垂直与平面N,则称向量n为平面N的法向量。
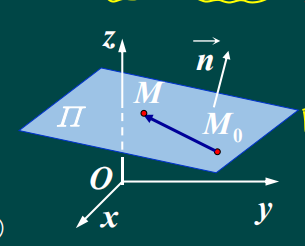
设一平面通过一直点 M 0 ( x 0 , y 0 , z 0 ) M_0(x_0,y_0,z_0) M0(x0,y0,z0)求垂直于非零向量 n ⃗ \vec{n} n= (A,B,C),求改平面N的方程。
任意点 M ( x , y , z ) ∈ N M(x,y,z) \in N M(x,y,z)∈N,则有 M 0 M ⃗ ⊥ n ⃗ \vec{M_0M} \bot \vec{n} M0M⊥n 故 M 0 M ⃗ . n ⃗ = 0 \vec{M_0M}.\vec{n}=0 M0M.n=0(两向量垂直相乘为:0)
↓ M 0 M ⃗ = ( x − x 0 , y − y 0 , z − z 0 ) \downarrow \qquad \vec{M_0M}=(x-x_0,y-y_0,z-z_0) ↓M0M=(x−x0,y−y0,z−z0)
A ( x − x 0 ) + B ( y − y o ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y-y_o)+C(z-z_0) = 0 A(x−x0)+B(y−yo)+C(z−z0)=0 ①
称 ① 式为平面N的点法式方程。
例1 求过三点 M 1 ( 2 , 3 , 2 ) , M 2 ( 3 , 3 , 3 ) , M 3 ( 4 , 5 , 5 ) M_1(2,3,2),M_2(3,3,3),M_3(4,5,5) M1(2,3,2),M2(3,3,3),M3(4,5,5) 的平面N的方程。
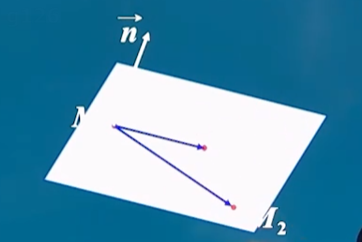
解: 取该平面N的法向量为:
n ⃗ = M 1 M 2 ⃗ ∗ M 1 M 3 ⃗ \vec{n}= \vec{M_1M_2} * \vec{M1M3} n=M1M2∗M1M3
又 M 1 ∈ N M_1\in N M1∈N,利用点法式的平面N的方程
14 ( x − 2 ) + 9 ( y + 1 ) − ( z − 4 ) = 0 14(x-2)+9(y+1)-(z-4)=0 14(x−2)+9(y+1)−(z−4)=0
即 14 x + 9 y − z − 15 = 0 14x+9y-z-15=0 14x+9y−z−15=0
2.平面的一般是方程
定义2 设有三元一次方程
A x + B y + C z + D = 0 ( A 2 + B 2 + C 2 ≠ 0 ) ② Ax+By+Cz+D=0 (A^2+B^2+C^2 \neq 0) ② Ax+By+Cz+D=0(A2+B2+C2=0)②
任取一组满足上述方程的数 x 0 , y 0 , z 0 x_0,y_0,z_0 x0,y0,z0,则:
A x 0 + B y 0 + C z 0 + D = 0 Ax_0+By_0+Cz_0+D=0 Ax0+By0+Cz0+D=0
以上两式相减,得平面的点法式方程
A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y-y_0)+C(z-z_0)=0 A(x−x0)+B(y−y0)+C(z−z0)=0
显然方程 ② 与此点法式方程等价,因此方程 ② 的图形是法向量为 n ⃗ = ( A , B , C ) \vec{n}=(A,B,C) n=(A,B,C)的平面,此方程为平行的一般式方程。
3.特殊位置的平面及方程
-
A x + B y + C z = 0表示通过原点的平面;
-
B y+C z+D = 0表示平行于 x 轴的平面;
-
A x+C z+D = 0表示平行于 y 轴的平面;
-
A x+B y+D = 0表示平行于 z 轴的平面;
-
A x + D = 0表示垂直于 x 轴的平面或平行于 Oyz 平面的平面;
-
B y + D = 0表示垂直于 y 轴的平面或平行于 Ozx 平面的平面;
-
C z + D = 0表示垂直于 z 轴的平面或平行于 Oxy 平面的平面。
-
B y +C z= 0表示通过 x 轴的平面;
-
A x+C z= 0表示通过 y 轴的平面;
-
A x+B y= 0表示通过 z 轴的平面。
例2 求过 z 轴和点 M ( 6 , 8 , 9 ) M(6,8,9) M(6,8,9)的平面 ∏ \prod ∏ 的方程。
解:由题可设平面 ∏ \prod ∏ 的方程为 A x+B y= 0。因为平面过点 M,所以 6 A + 8 B = 0 6A+8B=0 6A+8B=0,解得 A = − 4 3 B A=-\frac{4}{3}B A=−34B 。因此,平面 ∏ \prod ∏ 的方程是 − 4 3 x + y B = 0 {-\frac{4}{3}x+y}B=0 −34x+yB=0,即 (因 B ≠ \neq = 0 )。
4.平面的截距式方程
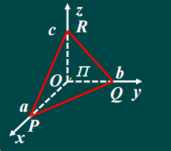
定义3 设平面的 ∏ \prod ∏与x,y,z轴分别交于P(a,0,0),Q(0,b,0),R(0,0,c)三点,则 ∏ \prod ∏的方程为
(a,b,c ≠ \neq = 0 ) x a + y b + z c = 1 \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 ax+by+cz=1 ③
称 ③ 式为平面 的截距式方程。
其中a,b,c分别称为平面 在x,y,z轴上的截距。
注:某平面具有截距式方程的充分必要条件:平面在三条坐标轴上的截距
均为非零常数。
5.两个平面的夹角
定义2 两平面 ∏ 1 , ∏ 2 \prod_1,\prod_2 ∏1,∏2的法线向量 的夹角 θ \theta θ(取锐角或直角)
称为这两个平面的夹角。
设平面 ∏ 1 \prod_1 ∏1的法向量为 n 1 ⃗ = ( A 1 , B 1 , C 1 ) \vec{n_1}=(A_1,B_1,C_1) n1=(A1,B1,C1)
设平面 ∏ 2 \prod_2 ∏2的法向量为 n 2 ⃗ = ( A 2 , B 2 , C 2 ) \vec{n_2}=(A_2,B_2,C_2) n2=(A2,B2,C2)
则两平面夹角 θ \theta θ的余弦为:
c o s θ = ∣ n 1 ⃗ . n 2 ⃗ ∣ ∣ n 1 ⃗ ∣ . ∣ n 2 ⃗ ∣ cos\theta=\frac{|\vec{n_1}.\vec{n_2}|}{|\vec{n_1}|.|\vec{n_2}|} cosθ=∣n1∣.∣n2∣∣n1.n2∣ 即
c o s θ = ∣ A 1 A 2 + B 1 B 2 + C 1 C 2 ∣ ∣ A 1 2 + B 1 2 + C 1 2 . A 2 2 + B 2 2 + C 2 2 ∣ cos\theta=\frac{|A_1A_2+B_1B_2+C_1C_2|}{|\sqrt{A_1^2+B_1^2+C_1^2}.\sqrt{A_2^2+B_2^2+C_2^2}|} cosθ=∣A12+B12+C12.A22+B22+C22∣∣A1A2+B1B2+C1C2∣
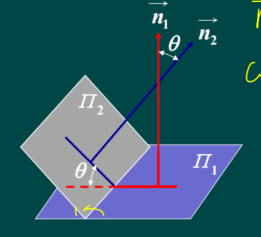
两个平面的夹角
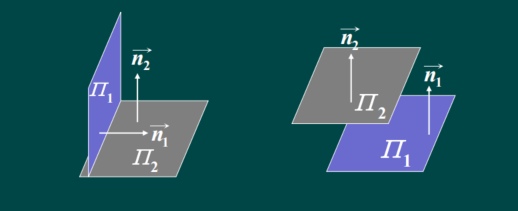
( 1 ) ∏ 1 ⊥ ∏ 2 (1) \prod_1\bot\prod_2 (1)∏1⊥∏2 => n 1 ⃗ ⊥ n 2 ⃗ \vec{n_1}\bot\vec{n_2} n1⊥n2 =>$ A_1A_2+B_1B_2+C_1C_2=0$
( 2 ) ∏ 1 / / ∏ 2 (2) \prod_1//\prod_2 (2)∏1//∏2 => n 1 ⃗ / / n 2 ⃗ \vec{n_1}//\vec{n_2} n1//n2 => A 1 A 2 = B 1 B 2 = C 1 C 2 \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2} A2A1=B2B1=C2C1
已知1平面 x + 2 y − z − 2 = 0 x+2y-z-2=0 x+2y−z−2=0和2平面 z x + y + z − 19 = 0 zx+y+z-19=0 zx+y+z−19=0 ,求这两个平面的夹角。
可得两个平面的法向量 $n_1 = 1,2,−1 , n_2 = 2,1,1 $
可得夹角的余弦 c o s θ = 3 6 . 6 = 1 2 cos\theta = \frac{3}{\sqrt{6}.\sqrt{6}}=\frac{1}{2} cosθ=6.63=21
这两个平面的夹角为 θ = π 6 \theta = \frac{\pi}{6} θ=6π
例4 设平面 ∏ \prod ∏垂直于平面 2 x + 3 y + 2 z = 0 2x+3y+2z=0 2x+3y+2z=0且过两点 M 1 ( 3 , 3 , 3 ) M_1(3,3,3) M1(3,3,3)和 M 2 ( 4 , 5 , 5 ) M_2(4,5,5) M2(4,5,5),求平面 ∏ \prod ∏方程。
解:已知平面的方程的法向量为 n 1 = ( 2 , 3 , 2 ) n_1= (2,3,2) n1=(2,3,2)
又有
M
1
M
2
=
(
1
,
2
,
2
)
M_1M_2=(1,2,2)
M1M2=(1,2,2) 在所求的平面上,则所求平面的法向量n同时垂直于向量
M
1
M
2
M_1M_2
M1M2 及
n
1
n_1
n1 ,因此可取平面
∏
\prod
∏的法向量为
n
⃗
=
n
1
∗
M
1
M
2
=
[
i
⃗
j
⃗
k
⃗
2
3
2
1
2
2
]
=
(
2
,
−
2
,
1
)
\vec{n}=n_1* M_1M_2= \left[ \begin{array}{c|c|c} \vec{i} & \vec{j} & \vec{k} \\ 2 & 3 & 2 \\ 1 & 2 & 2 \end{array} \right] = (2,-2,1)
n=n1∗M1M2=
i21j32k22
=(2,−2,1)
故所求平面的方程为
2
(
x
−
3
)
−
2
(
y
−
3
)
+
(
z
−
3
)
=
0
2(x-3)-2(y-3)+(z-3)=0
2(x−3)−2(y−3)+(z−3)=0
即 2 x − 2 y + z − 3 = 0 2x-2y+z-3=0 2x−2y+z−3=0
6.点到平面的距离公式
设 M 0 ( x 0 , y 0 , z 0 ) M_0(x_0,y_0,z_0) M0(x0,y0,z0)是平面Ax+By+Cz+D=0外的一点,则点 M 0 M_0 M0到平面的距离为
d = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 d=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}} d=A2+B2+C2∣Ax0+By0+Cz0+D∣
设平面法向量为 n ⃗ = ( A , B , C ) \vec{n}=(A,B,C) n=(A,B,C)令 M 0 M_0 M0在平面上的垂足 M 1 ( x 1 , y 1 , z 1 ) M_1(x_1,y_1,z_1) M1(x1,y1,z1),则 M 1 M_1 M1 到平面的距离为
d = ∣ M 1 M 0 ⃗ . n ⃗ ∣ n ⃗ d=\frac{|\vec{M_1M_0}.\vec{n}|}{\vec{n}} d=n∣M1M0.n∣
= ∣ A ( x 0 − x 1 ) + B ( y 0 − y 1 ) + C ( z 0 − z 1 ) ∣ A 2 + B 2 + C 2 ↓ 其中 A x 1 + B y 1 + C z 1 + D = 0 = \frac{|A(x_0-x_1)+B(y_0-y_1)+C(z_0-z_1)|}{\sqrt{A^2+B^2+C^2}} \downarrow 其中Ax_1+By_1+Cz_1+D=0 =A2+B2+C2∣A(x0−x1)+B(y0−y1)+C(z0−z1)∣↓其中Ax1+By1+Cz1+D=0
d = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 d=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}} d=A2+B2+C2∣Ax0+By0+Cz0+D∣
知识点3 点到平面的距离公式
例5 求点 P(1,2,3)到平面 2x-2y+z-3=0的距离d 。
解: d = ∣ 2 − 4 + 3 − 3 ∣ 2 2 + ( − 2 ) 2 + 1 2 = 2 3 d= \frac{|2-4+3-3|}{\sqrt{2^2+(-2)^2+1^2}} = \frac{2}{3} d=22+(−2)2+12∣2−4+3−3∣=32
知识点2 空间直线方程
1. 直线的一般式
定义:直线可视为两平面
∏
1
,
∏
2
\prod_1,\prod_2
∏1,∏2的交线,设平面
∏
1
,
∏
2
\prod_1,\prod_2
∏1,∏2的方程为
A
1
x
+
B
1
y
+
C
1
z
+
D
1
=
0
,
A
2
x
+
B
2
y
+
C
2
z
+
D
2
=
0
A_1x+B_1y+C_1z+D_1=0,A_2x+B_2y+C_2z+D_2=0
A1x+B1y+C1z+D1=0,A2x+B2y+C2z+D2=0则方程组:
{
A
1
x
+
B
1
y
+
C
1
z
+
D
1
=
0
A
2
x
+
B
2
y
+
C
2
z
=
D
2
=
0
\begin{cases} A_1x+B_1y+C_1z+D_1=0 \\ A_2x+B_2y+C_2z=D_2=0 \end{cases}
{A1x+B1y+C1z+D1=0A2x+B2y+C2z=D2=0
称该方程组为直线L的一般方程。

注:过某定直线的平面有无穷多个, 从中任选两个组成的方程组都是
交线的一般式方程,一般式方程不唯一。
2.直线的点向式方程
若非零向量S平行与直线L,则称S为直线的方向向量。
x − x 0 m = y − y 0 n = z − z 0 p \frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p} mx−x0=ny−y0=pz−z0
称上式为直线L的点向式方程。

点向式方程的特殊情况
当点向式中某些分母为零时,其分子也应理解为零。
如当
m
=
n
=
0
,
p
≠
0
m=n=0,p \neq 0
m=n=0,p=0时,直线方程为:
{
x
=
x
0
y
=
y
0
\begin{cases} x=x_0 \\ y=y_0 \end{cases}
{x=x0y=y0
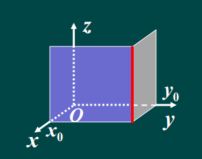
例1 已知直线I过点M(3,-2,6),且与平面x+3 =0 垂直,求直线L的方程解:因为直线 L 垂直于平面x+3=0,所以可取 L 的方向 s ⃗ = ( 1 , 0.0 ) \vec{s}=(1,0.0) s=(1,0.0)因此,所求直线 L 的点向式方程型如:
x − 3 1 = y + 2 0 = z − 6 0 \frac{x-3}{1}=\frac{y+2}{0}=\frac{z-6}{0} 1x−3=0y+2=0z−6
因此,所求直线转为一般式方程为:
{
y
=
−
2
z
=
6
\begin{cases} y=-2 \\ z=6 \end{cases}
{y=−2z=6
3.直线的两点式方程
定义3 设直线 L 过两点M1,M2,则直线 L 的方程为:
x − x 1 x 2 − x 1 = y − y 1 y 2 − y 1 = z − z 1 z 2 − z 1 \frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1} x2−x1x−x1=y2−y1y−y1=z2−z1z−z1
称方程组为直线 L 的两点式方程.
4.直线的参数式方程
若令 x − x 0 m = y − y 0 n = z − z 0 p = t \frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}=t mx−x0=ny−y0=pz−z0=t
的直线L的参数式方程:
{
x
=
x
0
+
m
t
y
=
y
0
+
n
t
z
=
z
0
+
p
t
,
t
∈
R
.
\begin{cases} x=x_0+mt \\ y=y_0+nt \\ z=z_0+pt \end{cases} ,t \in R.
⎩
⎨
⎧x=x0+mty=y0+ntz=z0+pt,t∈R.
例2 用一般式及参数式表示直线:
{
x
+
y
+
z
+
1
=
0
2
x
−
y
+
3
z
+
4
=
0
\begin{cases} x+y+z+1=0 \\ 2x-y+3z+4=0 \end{cases}
{x+y+z+1=02x−y+3z+4=0
解:先在直线上找一点令x = 1,解方程组:
{
y
+
z
=
−
2
y
−
3
z
=
6
\begin{cases} y+z=-2 \\ y-3z=6 \end{cases}
{y+z=−2y−3z=6
解得:y=0,z=-2
再求直线的方向向量 s ⃗ \vec{s} s.
因为所求直线L与已知两平面的法向量
n
1
⃗
=
(
1
,
1
,
1
)
\vec{n_1}= (1,1,1)
n1=(1,1,1),
n
2
=
(
2
,
−
1
,
3
)
n_2=(2,-1,3)
n2=(2,−1,3)均垂直,所以可取所求直线的方向向量:
s
⃗
=
n
1
⃗
∗
n
2
⃗
=
[
i
⃗
j
⃗
k
⃗
1
1
1
2
−
1
3
]
=
(
4
,
−
1
,
−
3
)
\vec{s}=\vec{n_1}*\vec{n_2}= \left[ \begin{array}{c|c|c} \vec{i} & \vec{j} & \vec{k} \\ 1 & 1 & 1 \\ 2 & -1 & 3 \end{array} \right] =(4,-1,-3)
s=n1∗n2=
i12j1−1k13
=(4,−1,−3)
故所给直线的点向式方程为:
x
−
1
4
=
y
−
1
=
z
+
2
−
3
=
t
\frac{x-1}{4}=\frac{y}{-1}=\frac{z+2}{-3}=t
4x−1=−1y=−3z+2=t
参数式方程为:
{
x
=
1
+
4
t
y
=
−
t
z
=
−
2
−
3
t
\begin{cases} x=1+4t\\ y=-t \\ z=-2-3t \end{cases}
⎩
⎨
⎧x=1+4ty=−tz=−2−3t
解题思路:
(1)先找直线上一点;
(2)再找直线的方向向量。
5.两条直线的夹角
1.两直线的夹角
定义5 两直线L1,L2的方向向量的夹角 θ \theta θ (取锐角或直角)称为这两条
直线的夹角。范围在 [ 0 , π 2 ] [0,\frac{\pi}{2}] [0,2π]
2.直线夹角的计算
设直线 L 1 L_1 L1的方向向量为 s 1 ⃗ = ( m 1 , n 1 , p 1 ) \vec{s_1}=(m_1,n_1,p_1) s1=(m1,n1,p1)
设直线 L 2 L_2 L2的方向向量为 s 2 ⃗ = ( m 2 , n 2 , p 2 ) \vec{s_2}=(m_2,n_2,p_2) s2=(m2,n2,p2)
则两直线夹角 的余弦为:
c o s θ = ∣ s 1 ⃗ . s 2 ⃗ ∣ ∣ s 1 ⃗ ∣ . ∣ s 2 ⃗ ∣ cos\theta=\frac{|\vec{s_1}.\vec{s_2}|}{|\vec{s_1}|.|\vec{s_2}|} cosθ=∣s1∣.∣s2∣∣s1.s2∣
即: c o s θ = ∣ m 1 m 2 + n 1 n 2 + z 1 z 2 ∣ m 1 2 + n 1 2 + p 1 2 m 2 2 + n 2 2 + p 2 2 cos\theta=\frac{|m_1m_2+n_1n_2+z_1z_2|}{\sqrt{m_1^2+n_1^2+p_1^2}\sqrt{m_2^2+n_2^2+p_2^2}} cosθ=m12+n12+p12m22+n22+p22∣m1m2+n1n2+z1z2∣
3.直线的特殊位置关系
(1) L 1 ⊥ L 2 − − > s 1 ⃗ ⊥ s 2 ⃗ − − > m 1 m 2 + n 1 n 2 + p 1 p 2 = 0 L_1\bot L_2 --> \vec{s_1}\bot\vec{s_2}--> m_1m_2+n_1n_2+p_1p_2=0 L1⊥L2−−>s1⊥s2−−>m1m2+n1n2+p1p2=0
(2) L 1 / / L 2 − − > s ⃗ / / s 2 ⃗ − − > m 1 m 2 = n 1 n 2 = p 1 p 2 L_1//L_2-->\vec{s}//\vec{s_2}-->\frac{m_1}{m_2}=\frac{n_1}{n_2}=\frac{p_1}{p_2} L1//L2−−>s//s2−−>m2m1=n2n1=p2p1
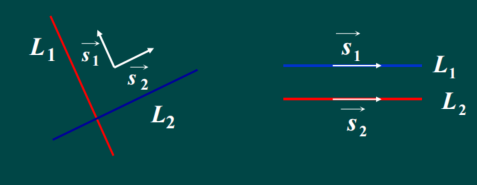
例3 已知直线 L1过点M(3,-2,6),并与直线 L平行,且直线
L
:
{
x
−
3
y
+
3
=
0
3
x
+
y
+
6
z
+
1
=
0
L: \begin{cases} x-3y+3=0 \\ 3x+y+6z+1=0 \end{cases}
L:{x−3y+3=03x+y+6z+1=0
求直线
L
1
L_1
L1的方程。
解:设
n
1
⃗
,
n
2
⃗
\vec{n_1},\vec{n_2}
n1,n2分别为 L 的方程所对应的两平面的法向量,显有
n
1
⃗
=
(
1
,
−
3
,
0
)
,
n
2
⃗
=
(
3
,
1
,
6
)
\vec{n_1}=(1,-3,0),\vec{n_2}=(3,1,6)
n1=(1,−3,0),n2=(3,1,6),因为L1//L3,则可取所求直线的一个方向向量
s
⃗
=
n
1
⃗
∗
n
2
⃗
=
[
i
⃗
j
⃗
k
⃗
1
−
3
0
3
1
6
]
=
(
−
18
,
−
6
,
10
)
=
2
(
−
9
,
−
3
,
5
)
\vec{s}=\vec{n_1}*\vec{n_2}= \left[ \begin{array}{c|c|c} \vec{i} & \vec{j} & \vec{k} \\ 1 & -3 & 0 \\ 3 & 1 & 6 \end{array} \right] =(-18,-6,10)=2(-9,-3,5)
s=n1∗n2=
i13j−31k06
=(−18,−6,10)=2(−9,−3,5)
利用点向式得所求直线的方程为:
x − 3 − 9 = y + 2 − 3 = z − 6 5 \frac{x-3}{-9}=\frac{y+2}{-3}=\frac{z-6}{5} −9x−3=−3y+2=5z−6
例4 求以下两直线的夹角
L
1
:
x
−
1
1
=
y
−
4
=
z
−
6
1
L_1: \frac{x-1}{1}=\frac{y}{-4}=\frac{z-6}{1}
L1:1x−1=−4y=1z−6
L
2
:
{
x
+
y
+
2
=
0
x
+
2
z
=
0
L2: \begin{cases} x+y+2=0 \\ x+2z=0 \end{cases}
L2:{x+y+2=0x+2z=0
解:直线L1的方向向量为
s
1
⃗
=
2
,
−
2
,
−
1
\vec{s_1}={2,-2,-1}
s1=2,−2,−1
直线L2的方向向量为:
s
2
⃗
=
[
i
⃗
j
⃗
k
⃗
1
1
0
1
0
2
]
=
(
2
,
−
2
,
−
1
)
\vec{s_2}= \left[ \begin{array}{c|c|c} \vec{i} & \vec{j} & \vec{k} \\ 1 & 1 & 0 \\ 1 & 0 & 2 \end{array} \right] =(2,-2,-1)
s2=
i11j10k02
=(2,−2,−1)
二直线夹角
ϑ
\vartheta
ϑ的余弦为:
c
o
s
ϑ
=
s
1
⃗
s
2
⃗
∣
s
1
⃗
∣
∣
s
2
⃗
∣
=
2
2
cos\vartheta=\frac{\vec{s_1}\vec{s_2}}{|\vec{s_1}||\vec{s_2}|}=\frac{\sqrt{2}}{2}
cosϑ=∣s1∣∣s2∣s1s2=22
从而
ϑ
=
π
4
\vartheta=\frac{\pi}{4}
ϑ=4π
6.直线与平面的夹角
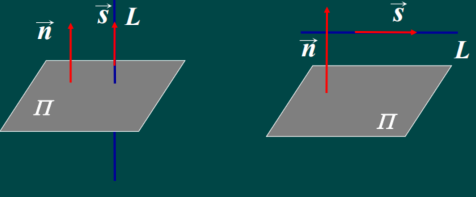
定义6 直线 L 与其在平面 ∏ \prod ∏ 内的投影直线 *L’*的夹角 ϑ \vartheta ϑ称为直线与平面的夹角。
1.直线夹角的计算
设直线 L的方向向量为 s ⃗ = ( m , n , p ) \vec{s}=(m,n,p) s=(m,n,p)
平面 ∏ \prod ∏的法向量 n ⃗ = ( A , B , C ) \vec{n}=(A,B,C) n=(A,B,C)
则直线与平面夹角
θ
\theta
θ的正弦为
s
i
n
θ
=
∣
c
o
s
(
n
⃗
,
s
⃗
)
∣
=
∣
n
⃗
.
s
⃗
∣
∣
n
⃗
∣
∣
s
⃗
∣
sin\theta=|cos(\vec{n},\vec{s})|=\frac{|\vec{n}.\vec{s}|}{|\vec{n}||\vec{s}|}
sinθ=∣cos(n,s)∣=∣n∣∣s∣∣n.s∣
即
s
i
n
θ
=
A
m
+
B
n
+
C
p
A
2
+
B
2
+
C
2
m
2
+
n
2
+
p
2
sin\theta=\frac{Am+Bn+Cp}{\sqrt{A^2+B^2+C^2}\sqrt{m^2+n^2+p^2}}
sinθ=A2+B2+C2m2+n2+p2Am+Bn+Cp
2.直线与平面的特殊位置关系
(1) L ⊥ ∏ − − > s ⃗ / / n ⃗ − − > s ⃗ n ⃗ = 0 − − > A m = B n = C p L\bot\prod --> \vec{s}//\vec{n}-->\vec{s}\vec{n}=0-->\frac{A}{m}=\frac{B}{n}=\frac{C}{p} L⊥∏−−>s//n−−>sn=0−−>mA=nB=pC
(2) L / / ∏ − − > s ⃗ ⊥ n ⃗ − − > s ⃗ . n ⃗ = 0 − − > A m + B n + C p = 0 L//\prod -- > \vec{s}\bot\vec{n} --> \vec{s}.\vec{n}=0--> Am+Bn+Cp=0 L//∏−−>s⊥n−−>s.n=0−−>Am+Bn+Cp=0
例5 求过点(1,-2,4)且与平面 2 x − 3 y + z − 4 = 0 2x-3y+z-4=0 2x−3y+z−4=0垂直的直线方程。
解:取已知平面的法向量 n ⃗ = ( 2 , − 3 , 1 ) \vec{n}=(2,-3,1) n=(2,−3,1)
为所求直线的方向向量。
则直线的点向式方程为
x − 1 2 = y + 2 − 3 = z − 4 1 \frac{x-1}{2}=\frac{y+2}{-3}=\frac{z-4}{1} 2x−1=−3y+2=1z−4
qrt{m2+n2+p^2}}$
2.直线与平面的特殊位置关系
(1) L ⊥ ∏ − − > s ⃗ / / n ⃗ − − > s ⃗ n ⃗ = 0 − − > A m = B n = C p L\bot\prod --> \vec{s}//\vec{n}-->\vec{s}\vec{n}=0-->\frac{A}{m}=\frac{B}{n}=\frac{C}{p} L⊥∏−−>s//n−−>sn=0−−>mA=nB=pC
(2) L / / ∏ − − > s ⃗ ⊥ n ⃗ − − > s ⃗ . n ⃗ = 0 − − > A m + B n + C p = 0 L//\prod -- > \vec{s}\bot\vec{n} --> \vec{s}.\vec{n}=0--> Am+Bn+Cp=0 L//∏−−>s⊥n−−>s.n=0−−>Am+Bn+Cp=0
[外链图片转存中…(img-ITGnnj8A-1694230678106)]
例5 求过点(1,-2,4)且与平面 2 x − 3 y + z − 4 = 0 2x-3y+z-4=0 2x−3y+z−4=0垂直的直线方程。
解:取已知平面的法向量 n ⃗ = ( 2 , − 3 , 1 ) \vec{n}=(2,-3,1) n=(2,−3,1)
为所求直线的方向向量。
则直线的点向式方程为
x − 1 2 = y + 2 − 3 = z − 4 1 \frac{x-1}{2}=\frac{y+2}{-3}=\frac{z-4}{1} 2x−1=−3y+2=1z−4