文章目录
- 前言
- 1. 树的常见概念
- 2. 树的性质
- 3. 树的定义与存储方式
- 4. 树的遍历方式
- 5. 通过序列构建二叉树
- 5.1 前中序列恢复二叉树
- 5.2 中后序列恢复二叉树
- 总结
前言
提示:瑞秋是个小甜心,她只喜欢被爱,不懂的去爱人。 --几米《你们 我们 他们》
树是一种非常重要的数据结构,在算法和工程中都有大量的应用,我们这里从概念一步一步学习,闯过这一关,掌握树的基本特征以及遍历方面的基础问题。
1. 树的常见概念
树是一个有n个有限节点组成一个具有层次关系的集合,每个节点有0个或者多个子节点,没有父节点的节点为称为根节点,也就是说除了根节点以为每个节点都有父节点,并且有且只有一个节点。树的种类有很多,最常见的就是二叉树了,基本结构如下:
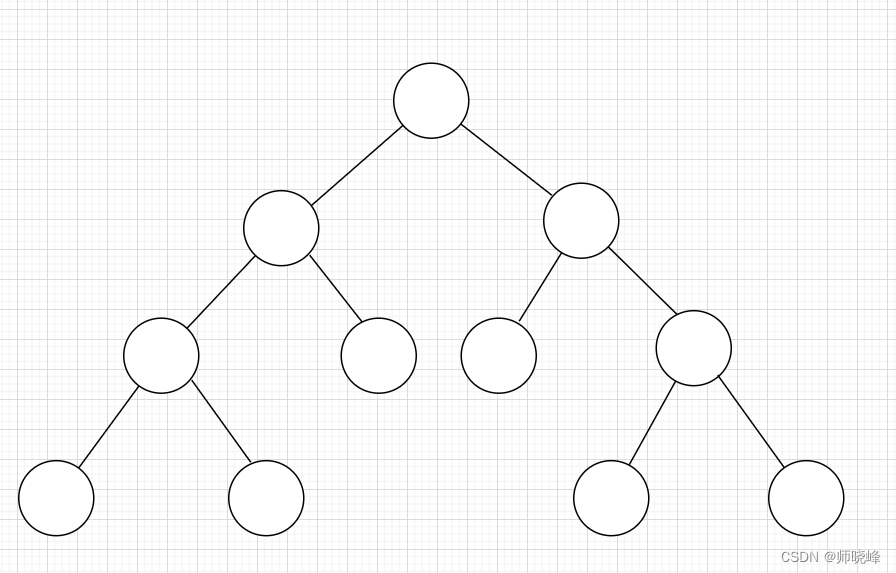
参考上面图的结构,可以很方面的理解树的概念:
- 节点的度:一个节点含有的几点的个数称为该节点的度
- 树的度:一颗树中,最大的节点的度称为树的度,注意与节点度的区别
- 叶节点或者终端节点:度为0的节点称为叶节点
- 非终端节点或者分支节点:度不为0的节点
- 双亲节点或者父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点
- 孩子节点或者子节点:一个节点含有的子树的根节点称为该节点的子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点
- 节点的祖先:从根节点到该节点所有分支上的所有节点
- 子孙:以某节点为根节的子树中任一节点都称为该节点的子孙
- 森林:有m(m >= 0 )课互不相交的树的集合称为森林
- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树
- 有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树
- 二叉树:每个节点最多含有两个子树的树称为二叉树
2. 树的性质
- 性质1:在二叉树的第i层上至多有2^(i - 1)个节点(i > 0)
- 性质2:深度为k的二叉树之多有2^k - 1 个节点(k > 0)
- 性质3:对于任意一颗二叉树,如果其叶节点数为N0,而度数为2的节点总数为N2,则N0 = N2 + 1
- 性质4:具有n个节点的完全二叉树的深度必为log2(n + 1)
- 性质5:对完全二叉树,若从上至下,从左至右编号,则编号为i的节点,其左孩子的编号一定是2i,其右孩子必是2i+ 1;其双亲的编号是i/2(i == 1 时为根,除外哈🤣)
满二叉树和完全二叉树是经常晕的问题,我们有必要单独看一下,满二叉树就是如果一棵二叉树只有度为0的节点和度为2的节点,而且度为0的节点在同一层,则这棵二叉树为满二叉树。
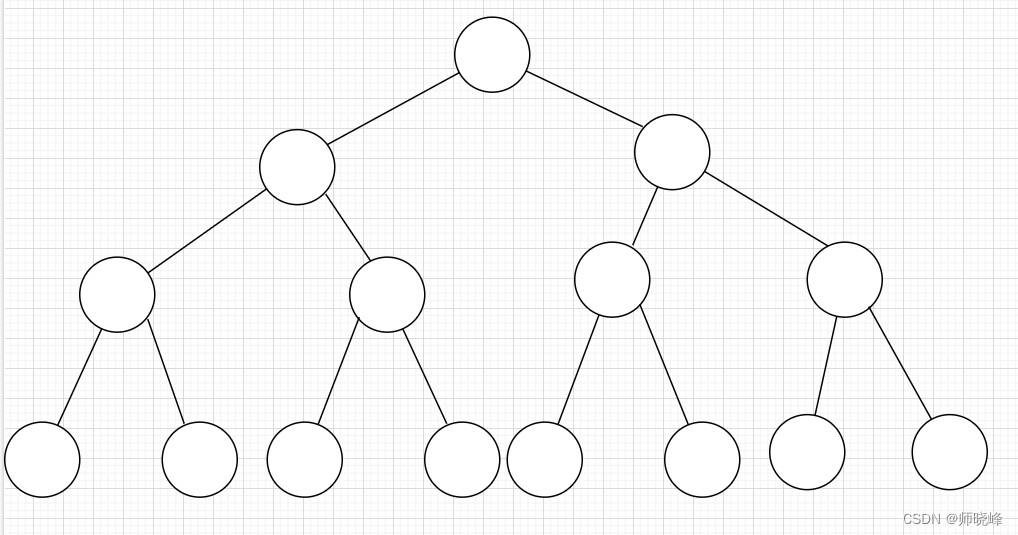
这颗二叉树为满二叉树,也可以说深度为k=4,有2^k -1 = 15个 节点的二叉树。
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没有填满外,其余每层节点点数都达到最大值,并且最下面一层的节点都集中在该层的最左侧的若干位置。
这个定义,就有些恶心了,估计大部分看了之后还是不懂什么是完全二叉树,看看下面的图:
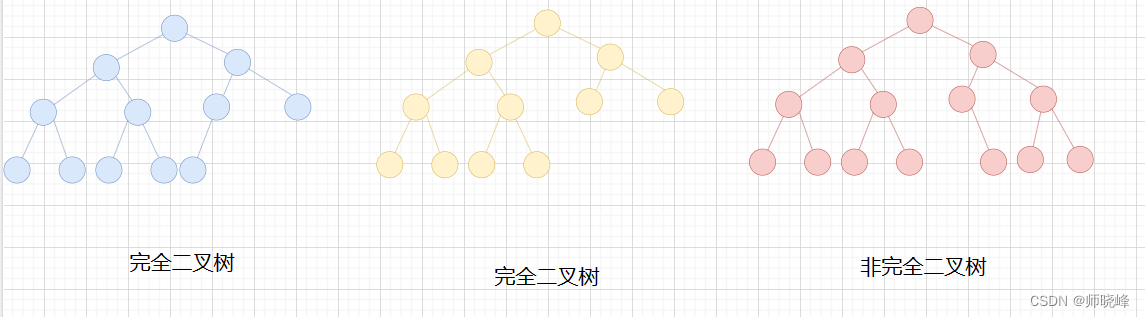
前面两棵树的前n-1层都是满的,最后一层所有子节点都集中在左侧区域,而且节点之间不能有间隙。最后一个为什么呢?他有一个节点缺少一个左子节点/
3. 树的定义与存储方式
注意:
这里我们主要看原理,不执行代码,采用伪代码的方式,理解方便一些
定义树的原理和前面讲的链表本质上差不多,只不过多了一个指针,如果是二叉树的化,只要在链表上的定义增加一个指针就可以了:
public class TreeNode{
int val;
TreeNode left;
TreeNode right;
}
这里本质上就是两个引用,分别指向两个位置,为了方便理解,我们称为左孩子和右孩子。如果是N叉树要如何定义呢?其实就是每个节点最多可以有N个节点指向其他位置,这里就不用left和right,我们使用List存储就行了,也就是如下:
// 定义N叉树
public class TreeNode {
int val;
List<TreeNode> nodes;
}
那么是否可以采用数组的方式存储二叉树呢?其实就是用数组来存储二叉树的,顺序存储的方式如图:
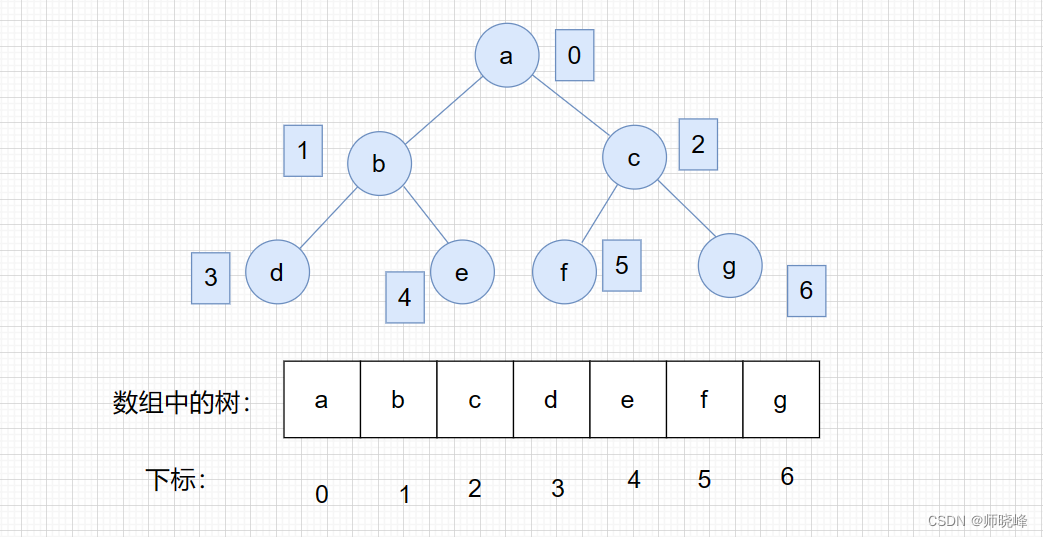
用数组来存储二叉树如何遍历呢?如果父节点的数组下标i,那么它的做还是就是 i* 2 + 1,右孩子就是 i * 2 + 2.
但是用链式表示二叉树,更方便我们理解,所以一般也采用链式二叉树。所以大家要知道一点,数组也是可以便是二叉树的。
使用数组存储的最大问题就是可能存在大量的空间浪费。如图上面假设b没有分支,那么数组1 3 4就空着,但是整个数组的大小仍然是7,因此很少使用数组来存储树。
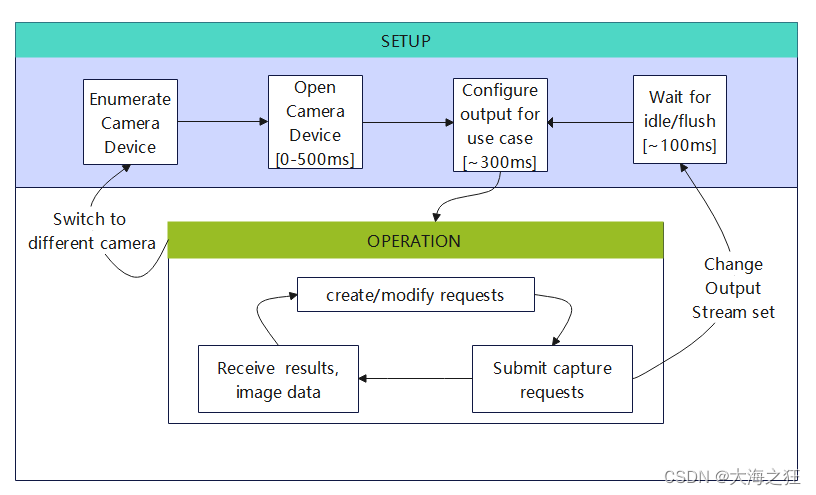
4. 树的遍历方式
我们常见的树的遍历方式,层次遍历和深度优先遍历两种:
- 深度优先遍历:先往深走,遇到叶子节点再往回走
- 广度优先遍历:一层一层的去遍历,一层遍历完再访问下一层
这两种遍历方式不仅仅是二叉树,N叉树也是,图结构也有,我们更常见的叫法:广度优先和深度优先,本质上是一回事。深度优先又有前中后三种,避免混淆,我们记住一点:前指的是中间的父节点再遍历中的顺序,只要明白了这一点,前中后序就是指中间节点的位置就可以了。
看如下中间节点的顺序,就可以发现问题,访问中间节点的顺序就是所谓的遍历方式
前序遍历:中左右
中序遍历:左中右
后序遍历:左右中
大家试着画图写一写,看看自己是否真的理解前中后序了。
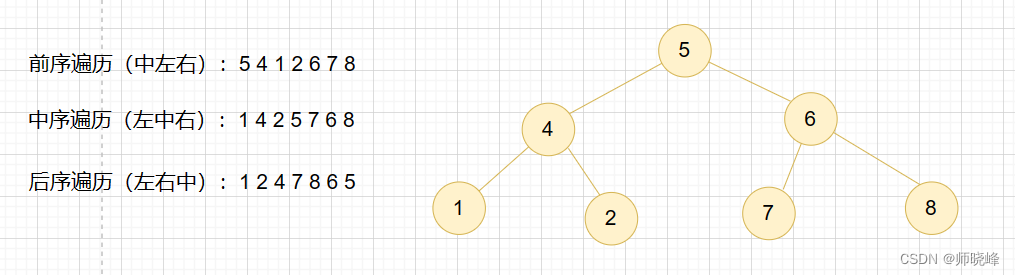
后面大量的算法都与这四种(层次,前中后)遍历方式有关,有的题目根据处理角度不同,可以用层次遍历,也可以用一种甚至两种深度优先的方式来实现。
5. 通过序列构建二叉树
前面我们已经介绍了怎么些前中后序的过程,这里我们看一看怎么通过序列来恢复原始二叉树:
前序遍历:中左右 [5 4 1 2 6 7 8]
中序遍历:左中右 [1 4 2 5 7 6 8]
后序遍历:左右中 [1 2 4 7 8 6 5]
5.1 前中序列恢复二叉树
我们先看看如何通过中前序列恢复二叉树:
前序遍历:中左右 [5 4 1 2 6 7 8]
中序遍历:左中右 [1 4 2 5 7 6 8]
- 第一轮
我们先从前序第一个就是访问根节点,所以根节点是5
中序遍历的特点是根节点的左子树的元素在根节点左侧,右子树的元素都在根节点右侧,从中序遍历序列我们可以划分成如下结构:
前序序列划分:
5 [ 4 1 2 ] [ 6 7 8 ]
中序序列划分:
[ 1 4 2 ] 5 [ 7 6 8 ]
当然前序序列第一个括号里面的都是左子树的元素,第二个括号一定都是右子树的元素。
那么这里怎么将这两个括号从哪里分开,我们彩照中序的两个数组划分。我们看前序2之前的元素都在第一个括号中,7之后的元素都在第二个数组中,所以这里从2和7之间划分。
由此我们画图表示一下,看下此时的树的结构:

- 第二轮:
我们先看两个序列的第一个数组
根据上面的划分方法:
前序序列划分:
4 [ 1 ] [ 2 ]
中序序列划分:
[ 1 ] 4 [ 2 ]
此时树的结构为:
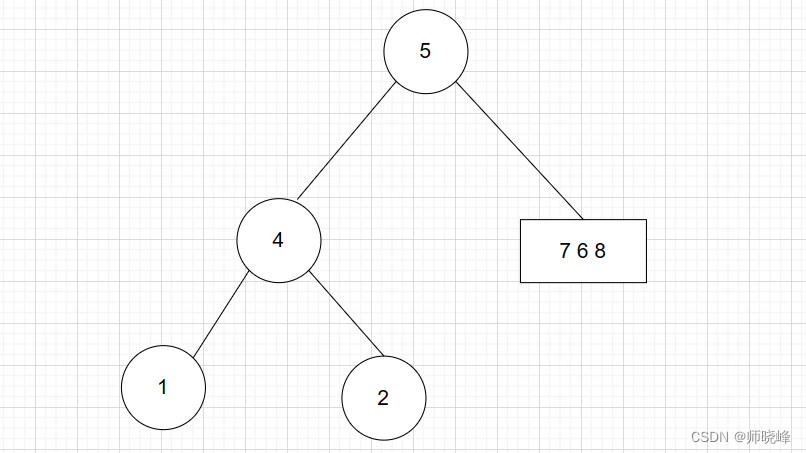
- 第三轮
我们看两个序列的第二个数组
根据上面的划分方法:
前序序列划分:
6 [ 7 ] [ 8 ]
中序序列划分:
[ 7 ] 6 [ 8 ]
此时树的结构为:
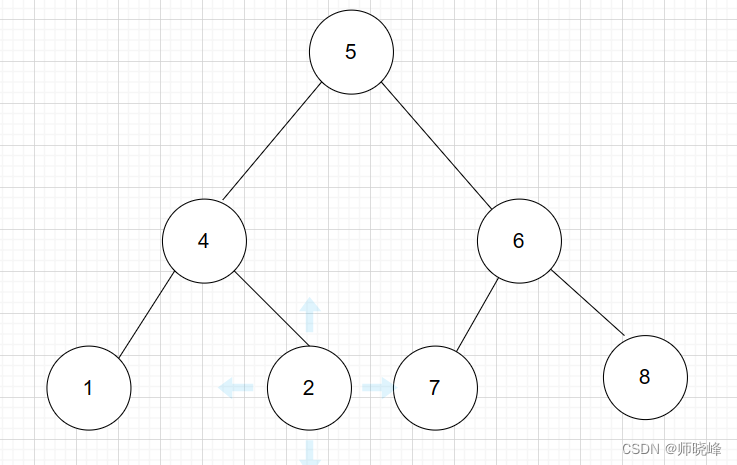
如此就是最终效果了,可以和上面的图对比一下。
5.2 中后序列恢复二叉树
通过中序和后序也能恢复原始序列,唯一不同的是后续的最后一个是根节点,中序的处理上面是一样的过程。
中序遍历:左中右 [1 4 2 5 7 6 8]
后序遍历:左右中 [1 2 4 7 8 6 5]
这里读者可以自行尝试,我这里不做赘述了。
Q&A💡:
那么有疑问了,为什么前序和后序不能恢复二叉树?
前序遍历:中左右 [5 4 1 2 6 7 8]
后序遍历:左右中 [1 2 4 7 8 6 5]
我们看前序和后序,通过前序我们可以知道根节点,通过后序我们也只能知道根节点,那么中间的部分要怎么划分呢?那些元素属于左子树,那些元素属于右子树呢?很显然,我们不得而知,所以用前序和后序不能恢复二叉树。
推荐力扣的题目⭐⭐⭐:
前序和中序造树:105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
中序和后序造树:106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
总结
提示:树的概念,二叉树、完全二叉树、满二叉树,树的恢复,前中后序序列