前言

完全背包；

一、70. 爬楼梯（进阶）

第44天的blog里面有提到这个题目，本质上还是完全背包；另外，例子中有重复，所以是排列，并且背包在前面；

class Solution {
    public int climbStairs(int n) {
       //背包 n ; 物品 台阶（1,2），重量和价值都是1,2
       //先背后物
       //dp[]表示有多少种方法能够到达某个位置，要求的是dp[n]
       //初始化 dp[0] = 1;因为它是基础
       
       int[] dp = new int[n+1];
       int m = 2;
       dp[0] = 1;
       
       for(int i = 1;i<=n;i++){
           for(int j = 1;j<=m;j++){
               if(i>=j){
                   dp[i] += dp[i-j];
               } 
           }
       }
       return dp[n];
    }
}

二、322. 零钱兑换

与昨天的形成对比，今天问的是最小个数：

动规五部曲分析如下：

确定dp数组以及下标的含义

dp[j]：凑足总额为j所需钱币的最少个数为dp[j]

确定递推公式

凑足总额为j - coins[i]的最少个数为dp[j - coins[i]]，那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]（考虑coins[i]）

所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。

递推公式：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);

dp数组如何初始化

首先凑足总金额为0所需钱币的个数一定是0，那么dp[0] = 0;

其他下标对应的数值呢？

考虑到递推公式的特性，dp[j]必须初始化为一个最大的数，否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。

所以下标非0的元素都是应该是最大值。

确定遍历顺序

本题求钱币最小个数，那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数。

所以本题并不强调集合是组合还是排列。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

所以本题的两个for循环的关系是：外层for循环遍历物品，内层for遍历背包或者外层for遍历背包，内层for循环遍历物品都是可以的！

举例推导dp数组

代码需要注意不少，和以前max相比需要很多改动：

//只有dp[j-coins[i]]不是初始最大值时，该位才有选择的必要;

class Solution {
    public int coinChange(int[] coins, int amount) {
        int max = Integer.MAX_VALUE;
        int[] dp = new int[amount + 1];
        //初始化dp数组为最大值
        for (int j = 0; j < dp.length; j++) {
            dp[j] = max;
        }
        //当金额为0时需要的硬币数目为0
        dp[0] = 0;
        for (int i = 0; i < coins.length; i++) {
            //正序遍历：完全背包每个硬币可以选择多次
            for (int j = coins[i]; j <= amount; j++) {
                //只有dp[j-coins[i]]不是初始最大值时，该位才有选择的必要
                if (dp[j - coins[i]] != max) {
                    //选择硬币数目最小的情况
                    dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
                }
            }
        }
        return dp[amount] == max ? -1 : dp[amount];
    }
}

三、279.完全平方数

if (dp[j - i * i] != max) {
      dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
}

class Solution {
    // 版本一，先遍历物品, 再遍历背包
    public int numSquares(int n) {
        int max = Integer.MAX_VALUE;
        int[] dp = new int[n + 1];
        //初始化
        for (int j = 0; j <= n; j++) {
            dp[j] = max;
        }
	//如果不想要寫for-loop填充數組的話，也可以用JAVA內建的Arrays.fill()函數。
	//Arrays.fill(dp, Integer.MAX_VALUE);
	
        //当和为0时，组合的个数为0
        dp[0] = 0;
        // 遍历物品
        for (int i = 1; i * i <= n; i++) {
            // 遍历背包
            for (int j = i * i; j <= n; j++) {
                //if (dp[j - i * i] != max) {
                    dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
                //}
		//不需要這個if statement，因爲在完全平方數這一題不會有"湊不成"的狀況發生（ 一定可以用"1"來組成任何一個n），故comment掉這個if statement。
            }
        }
        return dp[n];
    }
}

四、322和279 if的存在性

322：

if(dp[j-coins[i]] != max){

dp[j] = Math.min(dp[j-coins[i]] +1,dp[j]);

}

279：

//if (dp[j - i * i] != max) {
                    dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
                //}
       //不需要這個if statement，因爲在完全平方數這一題不會有"湊不成"的狀況發生（一定可以用"1"來組成任何一個n），故comment掉這個if statement。

倘若322没有if，结果是示例2有问题：

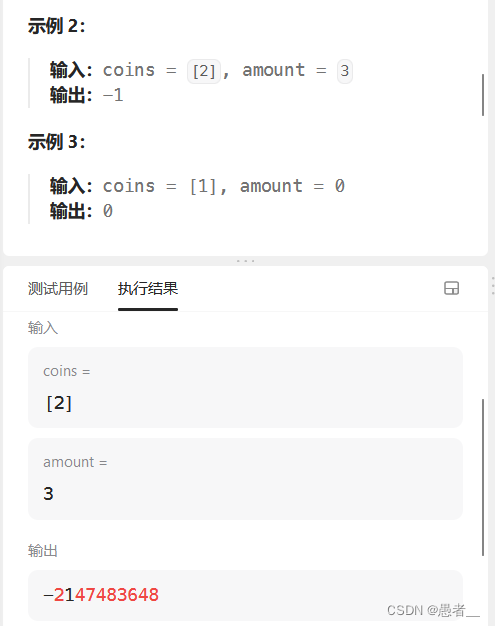
-2147483648是Integer的最小值，之所以这样，是因为max定义为最大值，而Integer.MAX_VALUE 加1溢出了，变成了最小值（为什么+1，可以写一下dp[]）；可以把max定义为最大值减一来避免这个问题或者在循环中加if判断；如下：

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount+1];
        int max = Integer.MAX_VALUE-1;
        for(int i =0;i<dp.length;i++){
            dp[i] = max;
        }
        dp[0] = 0;
        for(int i = 0;i<coins.length;i++){
            for(int j = coins[i];j <= amount;j++){
                // if(dp[j-coins[i]] != max){
                    dp[j] = Math.min(dp[j-coins[i]] +1,dp[j]);
                // }
                
            }
        }
        return dp[amount] == max?-1:dp[amount];
    }
}