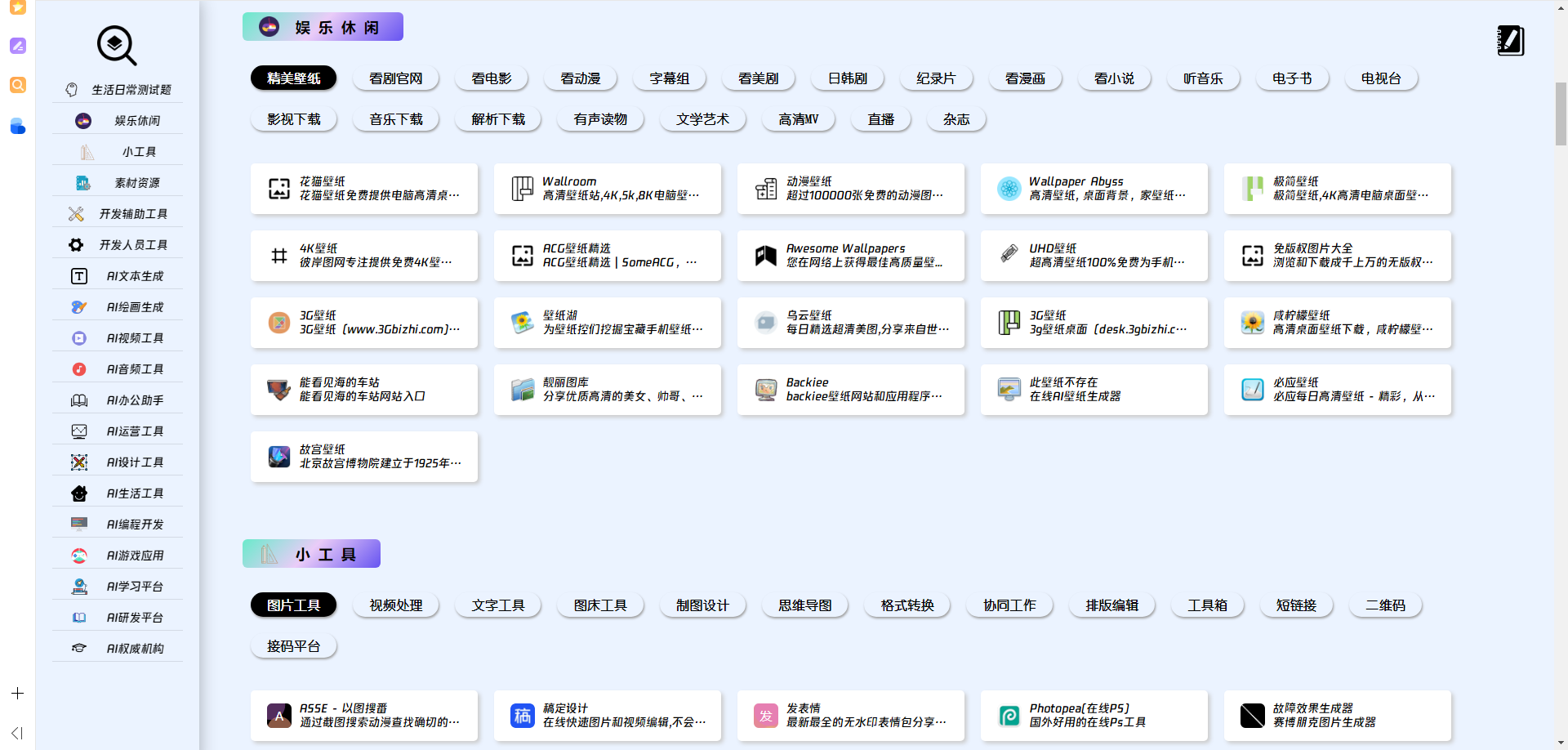
理解递归

递归的两个特点

• 调用自身
• 结束条件

举个从小就听过的例子：

1. 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：

2. 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：

3. 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：

4. 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：

4.“太困了不讲了”，于是都回去睡觉了。

3. 于是都回去睡觉了。

2. 于是都回去睡觉了。

1. 于是都回去睡觉了。

我晕，怎么讲了那么多故事，其实不然，我用不同颜色标记处来了每一层的对应关系，
很明显地看出颜色从头开始往中间逐渐变化，然后到一定程度（我们称之为递归的边界或是结束条件）就从内二外的层层返回。
这就是递归
类似于剥洋葱，一层套着一层，直到掰到最里层。

接着看下面的例子：

这句吓得我抱起了抱着抱着抱着我的小鲤鱼的我的我的我如果从字面意义上看可能看不出是什么意思，那么我们可以通过代码来实现同样的效果:

void digui(int n){
	cout << "抱着";
	if(!n){
		cout << "我的小鲤鱼";
	}
	else{
		digui(n - 1);
	}  
	cout << "的我";
	return;
}
int main(){
	cout << "吓得我抱起了";
	digui(2);
	return 0; 
}

计算n的阶乘

迭代版

n = 7
result = 1

for i in range(1, 7):
    res = result * i
    print(res)

1的阶乘等于1

2的阶乘等 1的阶乘 乘以2 等于2

3的阶乘等于 2的阶乘 乘以3 等于6

依次类推，就可以求出4，5，n的阶乘

我们在设计迭代算法的时候，使用的正向思维的方式

递归的思维正好相反，属于逆向思维

我们想计算5的阶乘

这个时候多么希望已经计算好了4的阶乘

然后在4的阶乘的基础上 乘以5 就是5的阶乘

但是4的阶乘我们不知道，继续向前希望求出3的阶乘 乘以4 得到4的阶乘

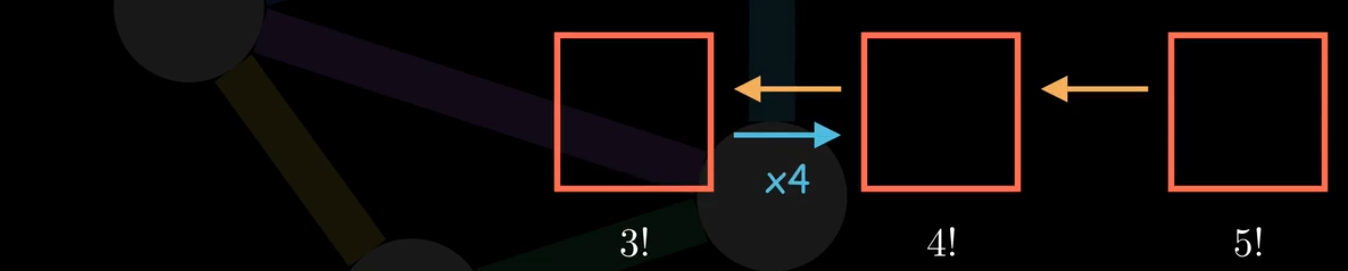
依此类推，不断向前推出到0的阶乘，1的阶乘等于1

这样后面所有的阶乘结果，都可以算出来。

这就是递归的逆向思维方式

即从 最终想要的答案出发
逐步向前寻找 上一层的答案
并且 用他们构造 当前层的答案
直到找到最深的那一层，问题的答案足够简单
递归执行便开始返回，并将每层的答案依次填上

def factorial(n):
    if n == 0:
        return 1
    tmp = factorial(n - 1)
    return tmp * n

迭代和递归的区别