1.空间直角坐标系的建立
三维空间中几何
空间图形形式 ----- 点 线 面 体
↑ ↓ \uparrow\downarrow ↑↓ (空间直角坐标系作为桥梁帮助我们理解)
代数理论表达 — 坐标,方程(组)
2. 空间直角坐标系的定义
定义: 过空间一定点O,过该点作三条相互垂直的有向线段,OX,OY,OZ,组成一个空间直角坐标系,记为:Oxyz。
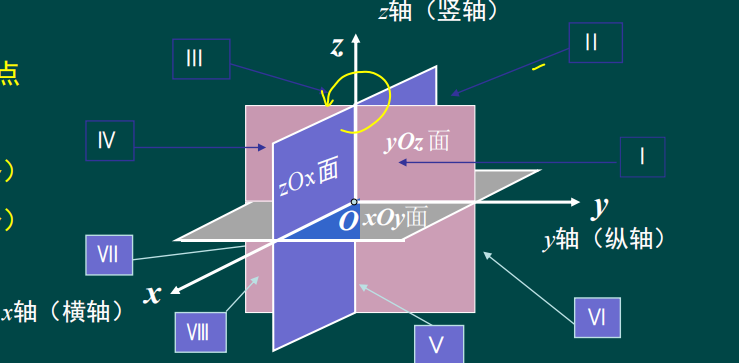
坐标系特点
-
坐标原点
-
坐标轴(三个)
-
坐标面(三个)
-
卦限(8个)
3. 空间点的坐标
定义:设M为空间的一点,过该点作三个分别垂直于x,y,z轴的平面,且分别交于点P,Q,R .若线段OP,OQ,OR的长度分别为, 则点M与一个三元有序数组(x , y , z )之间建立了一一对应的关系。称该三元有序数组(x , y , z )为点M的坐标。
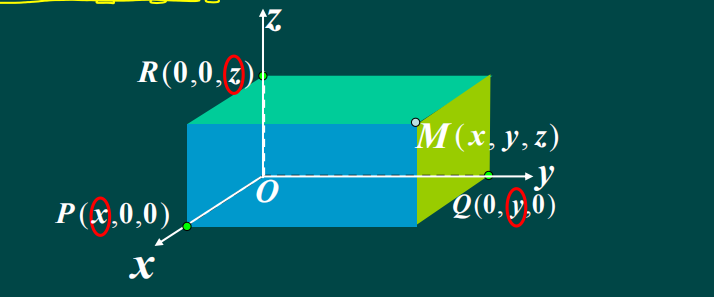
4.特殊点的坐标
-
坐标原点O (三项为零)
-
坐标轴上的点(三类)P Q R (两项为零)
-
坐标面上的点(三类)A B C (一项为零)
-
卦限上的点,如:第一卦限的点,各分量全为正
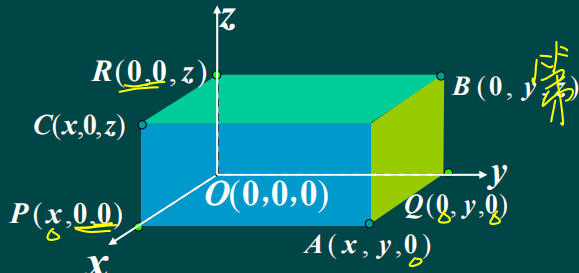
空间中两点间的距离公式
定理:设有空间两点M1(x1,y1,z1),M2(x2,y2,z2),则两点间的距离为
d=|M1M2|= ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 \sqrt{(x1-x2)^2 + (y1-y2)^2+(z1-z2)^2} (x1−x2)2+(y1−y2)2+(z1−z2)2
注:
(1) 任意点M(x,y,z)与坐标原点间的距离为:
d=|OM|= x 2 + y 2 + z 2 \sqrt{x^2+y^2+z^2} x2+y2+z2
(2)平面上任意两点间的距离为
d = |M1M2| = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 \sqrt{(x1-x2)^2+(y1-y2)^2} (x1−x2)2+(y1−y2)2
任意两点间的距离为
d = |M1M2| = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 \sqrt{(x1-x2)^2+(y1-y2)^2} (x1−x2)2+(y1−y2)2