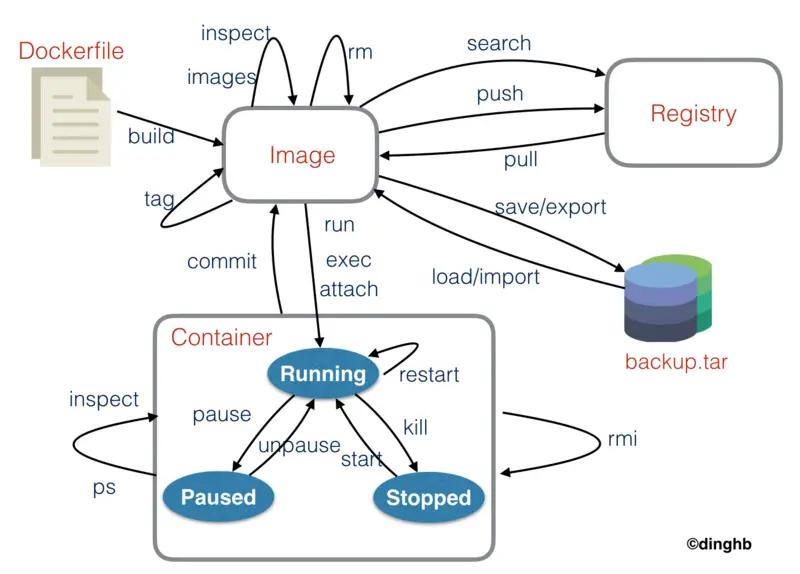
超图聚类论文阅读2：Last-step算法

《使用超图模块化的社区检测算法》

《Community Detection Algorithm Using Hypergraph Modularity》

COMPLEX NETWORKS 2021, SCI 3区

具体实现源码见HyperNetX库

工作：提出了一种用于超图的社区检测算法。该算法的主要特点是它可以根据一个社区中的顶点与其他社区中的顶点共享超边的频率进行调整以适应各种场景。

动机和贡献

复杂网络中的社区发现——超图社区发现

理论和工具的发展还不够充分，无法在超图情况下直接解决包括聚类在内的大多数问题。
研究者经常创建感兴趣的超图的 2 部图（即，用团替换每个超边）。移动到 2-section 图后，人们显然失去了一些关于尺寸大于 2 的超边的信息，因此人们普遍认为，利用原始超图的知识可以做得更好。

相关工作：

Kumar 等人仍然将问题简化为图，但使用原始超图迭代调整权重以鼓励某些超边包含在某些聚类中但不鼓励其他超边
作者自己在之前提出了图的经典空模型的许多超图扩展，这些扩展可能被真正的超图算法使用

本文贡献：提出了一个能够适应上述各种场景的框架

将图模块化函数的所有扩展推广和统一到超图，并将它们放入一个框架中来实现这一点
不同“切片”的贡献由可以针对给定场景调整的超参数控制（第2节）
提出了两种原型算法来展示框架的潜力，即所谓的概念验证（第 3 节）
引入了一个可能具有独立兴趣的合成随机超图模型，以测试算法在各种场景中的性能（第 4 节）
试验了我们的原型以及该领域的两个主要竞争对手，即 Louvain 和 Kumar 等（第 5 节）
- 适当调整超参数后，所提出的原型工作得很好
- 提供了这样的调整可以以无监督的方式进行的证据
揭示更多关于该效果的细节（第 6 节）

模块度函数

我们进一步概括了超图模块化函数，使我们能够以不同的方式评估对模块化函数的各种贡献

图模块度

G = (V, E)、n = |V|、度：degG(v)、社区A的体积

模块化函数有利于图 G 的顶点集的分区，其中大部分边完全落在parts（通常称为簇）内
benchmark是用Chung-Lu 随机图模型生成的图具有完全遵循 G 中的度序列的随机图上相连的情况

给定分区A：边贡献+度税
$q_G(\mathbf{A})=\sum_{A_i \in \mathbf{A}} \frac{e_G\left(A_i\right)}{|E|}-\sum_{A_i \in \mathbf{A}}\left(\frac{\operatorname{vol}_G\left(A_i\right)}{\operatorname{vol}_G(V)}\right)^2$

qG(A) ≤ 1
一个分区的话，值为0；一个点是一个分区的话，值小于0
找到最大模块度的分区——接近1
如果 q*(G) 接近于零（这是平凡的下界），则不存在社区结构

超图模块度

可以推广成二部图进行计算，每条边的权重为w(e)/(|e| − 1)

这种选择可确保创建的图的度分布与原始超图相同
它也很好地将 H 上的自然随机游走转换为相应 H[2] 上的随机游走
此过程会创建多重图

H = (V, E)、degH(v)、volH(A)

超图模块化函数的选择并不是唯一的。这取决于人们有多强烈地相信超边是其某些顶点落入一个社区的指标。即超边对社区的贡献

超边的所有顶点都必须属于其中一个部分
如果超边超过 50% 的顶点属于分区，则超边对这个分区有贡献
超边可能有助于对应于最大部分顶点属于的分区

majority-based modularity：

Bin(d, p) 表示具有参数 d 和 p 的二项式随机变量
$q_H^m(\mathbf{A})=\sum_{A_i \in \mathbf{A}} \frac{e_H^m\left(A_i\right)}{|E|}-\sum_{d \geq 2} \frac{\left|E_d\right|}{|E|} \sum_{A_i \in \mathbf{A}} \mathrm{P}\left(\operatorname{Bin}\left(d, \frac{\operatorname{vol}_H\left(A_i\right)}{\operatorname{vol}_H(V)}\right)>\frac{d}{2}\right)$
strict-based modularity：
$\begin{aligned} q_H^s(\mathbf{A}) & =\sum_{A_i \in \mathbf{A}} \frac{e_H^s\left(A_i\right)}{|E|}-\sum_{d \geq 2} \frac{\left|E_d\right|}{|E|} \sum_{A_i \in \mathbf{A}}\left(\frac{\operatorname{vol}_H\left(A_i\right)}{\operatorname{vol}_H(V)}\right)^d \\ & =\sum_{A_i \in \mathbf{A}} \frac{e_H^s\left(A_i\right)}{|E|}-\sum_{d \geq 2} \frac{\left|E_d\right|}{|E|} \sum_{A_i \in \mathbf{A}} \mathrm{P}\left(\operatorname{Bin}\left(d, \frac{\operatorname{vol}_H\left(A_i\right)}{\operatorname{vol}_H(V)}\right)=d\right) \end{aligned}$
——emH(Ai) 计算大多数顶点属于部分 Ai 的超边数，而在 (3) 中，esH(Ai) 计算所有顶点都属于部分 Ai 的超边数

统一和泛化：

独立处理来自大小为 d 的超边对模块化函数的贡献，分别考虑超边内包含在社区的节点恰好为c的情况

上面的多数模块度可以写成：
$q_H^m(\mathbf{A})=\sum_{A_i \in \mathbf{A}} \sum_{d \geq 2} \sum_{c=\lfloor d / 2\rfloor+1}^d\left(\frac{e_H^{d, c}\left(A_i\right)}{|E|}-\frac{\left|E_d\right|}{|E|} \cdot \mathrm{P}\left(\operatorname{Bin}\left(d, \frac{\operatorname{vol}_H\left(A_i\right)}{\operatorname{vol}_H(V)}\right)=c\right)\right)$
ed,c H (Ai) 是Ai 中恰好有 c 个成员的大小为 d 的超边的数量

可以写成：
$q_H^m(\mathbf{A})=\sum_{d \geq 2} \sum_{c=\lfloor d / 2\rfloor+1}^d q_H^{c, d}(\mathbf{A})$
其中定义一个“切片”：
$q_H^{c, d}(\mathbf{A})=\frac{1}{|E|} \sum_{A_i \in \mathbf{A}}\left(e_H^{d, c}\left(A_i\right)-\left|E_d\right| \cdot \mathrm{P}\left(\operatorname{Bin}\left(d, \frac{\operatorname{vol}\left(A_i\right)}{\operatorname{vol}(V)}\right)=c\right)\right)$
严格模块度可写成：
$q_H^s(\mathbf{A})=\sum_{d \geq 2} q_H^{d, d}(\mathbf{A})$
——多数超图模块度中每个“切片”的权重相等，而对于基于严格的定义模块度，仅考虑 c = d 的切片

新模块化函数由超参数 wc,d ∈ [0, 1] (d ≥ 2, [d/2] + 1 ≤ c ≤ d) 控制

给出广义超图模块度统一定义：
$q_H(\mathbf{A})=\sum_{d \geq 2} \sum_{c=\lfloor d / 2\rfloor+1}^d w_{c, d} q_H^{c, d}(\mathbf{A})$
$\alpha \in[0, \infty)$ , and $\rho_{\min }, \rho_{\max } \in(0.5,1]$ $\rho_{\min } \leq \rho_{\max } $
$w_{c, d}= \begin{cases}(c / d)^\alpha & \text { if }\left\lceil d \rho_{\min }\right\rceil \leq c \leq\left\lceil d \rho_{\max }\right\rceil \\ 0 & \text { otherwise }\end{cases}$
该定义为我们提供了更大的灵活性，并允许对某些切片的估值高于其他切片。

参数 ρmin 和 ρmax 分别与超边的最小和最大“纯度”假设相关，并取决于网络的同质性水平
参数 α 控制不同“纯度”级别的贡献超边之间的相对信息量之间的平滑过渡

在相应地调整超参数之后，广义模块度可以用于两种极端情况（基于多数和基于严格）以及介于两者之间的任何情况。

此外，广义模块度可以很好地近似对应的 2 部分图 H[2] 的图模块性。

算法

经典

Louvain：通过考虑其 2 部分（加权）图 H[2] 将问题简化为图，然后尝试找到最大化图模块性函数的分区

它是一种层次聚类算法，试图优化模块化功能（模块化优化阶段），将社区合并为单个顶点（社区聚合阶段），然后递归地对压缩图执行模块化聚类，直到无法增加模块化为止。
- 所有的聚类算法在本质上都是启发式的，只旨在找到“足够好”的分区，而不希望找到最好的分区。
- Louvain 是一种随机算法，在模块化优化阶段发生之前随机排序所有顶点。不幸的是，这意味着该算法不稳定，并且其结果在独立运行之间可能会有很大差异。
- 为了解决这个问题，可以改用图的集成聚类算法（ECG）。该算法以 Louvain 算法和共识聚类的概念为基础，具有良好的稳定性。
Kumar：以下改进通常会在几个合成和真实示例中给出比原始 Louvain 算法更好的结果。

该算法并不是真正基于超图的，而应该被视为由原始超图引导的基于图的方法的改进
- 首先在原始超图H的基础上构建一个保度加权图G
- 将Louvain算法应用于G，试图最大化图模块函数
- 重新访问超图 H 并根据它们对所获得部分之间的同质性的度量对超边进行仔细的重新加权。
- 重复这些步骤直到收敛。

LS and HA

传统方法总结：所有基于图模块化优化的成功算法（包括上文提到的 Louvain、ECG 和 Kumar 等）都是以相同的方式开始的。顶点最初自己是一个簇，若模块度增加则将顶点的集群更改为其邻居之一。

——超图中此方法的问题：那么只改变一个顶点的集群可能不会对模块化函数产生积极影响，除非存在小尺寸边。

算法：使用普通图模块化函数 qG(A) 进行“从地面提升过程”，再切换到超图对应函数 qH(A)

——两种， (HA) 尽快切换到超图、 (LS) 停留在图上的时间更长

HA（混合算法）：
1. 通过在从 H 构建的保度图 G 上使用 qG(A) 运行 ECG 来形成小而紧密的团块。修剪低于 70%（投票数）阈值的边，并将连通分量保留为初始团块。
2. 如果 qH(A) 提高，则合并团块（以随机顺序）。重复直到无法再改进为止。
3. 一次将一个顶点（以随机顺序）移动到相邻的簇，如果它提高了 qH则保留。重复直到收敛。
LS（最后一步）：
1. 运行 Kumar 算法
2. 只执行上面的最后一步（步骤 3.）

给出三个参数传入两种算法中：HA(α, ρmin, ρmax) 和 LS(α, ρmin, ρmax)

合成随机超图模型

经典随机图模型：

众所周知和广泛使用的 LFR 基准图
作者自己开发的ABCD

提出了一个受经典随机块模型启发的模型

模型特征：所提出的模型旨在简单，但它试图捕捉这样一个事实，即许多以超图表示的现实世界网络表现出不同程度的同质性或缺乏同质性。它为我们提供了一个工具来测试我们的算法在各种场景下的性能。一个好的算法应该能够以无监督的方式适应任何场景。

实验

设置合适的参数将对算法效果产生积极影响

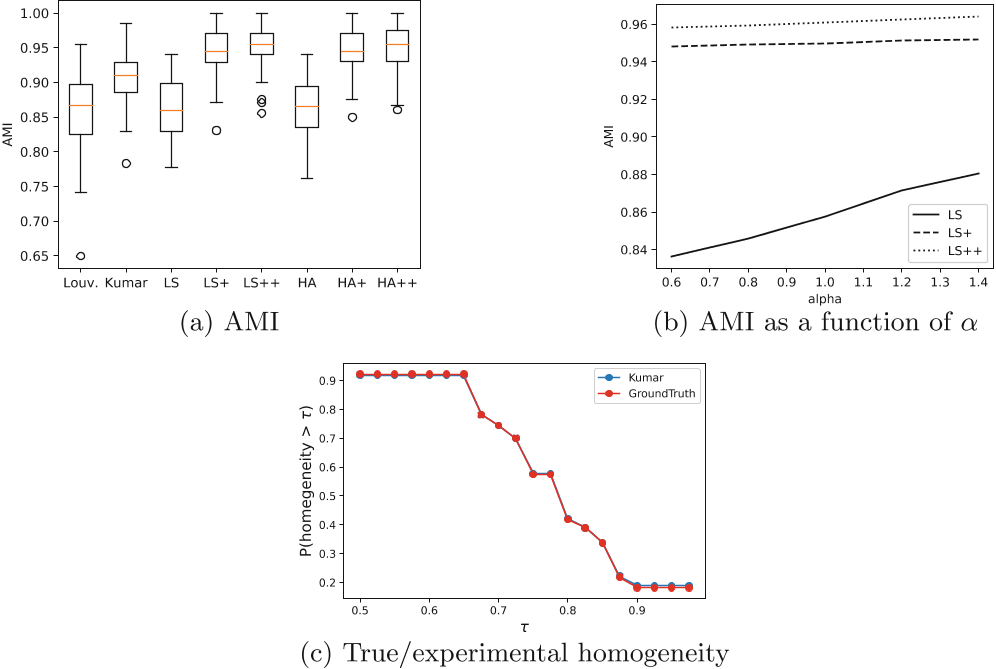
结论和未来方向

提出了两种原型算法并做了一些简单的实验来展示它们的潜力
- 展示了我们的原型算法工作得很好，但只有在对超参数进行适当调整后才能工作
- 初步实验表明，这种调整可以以无人监督的方式完成，但细节需要修复，并且需要解决过拟合问题
提出了两种方法来解决任何基于超图模块化函数的算法的初始阶段问题
1. 将 2-section 图的顶点嵌入到几何空间中，使用具有较大 k 值的经典 k-means 算法来找到初始分区
2. Kumar 等人提出的 Hyperedge 重新加权方案似乎效果很好，可以很容易地合并到我们的框架中。我们的目标是建立一个灵活的框架，该框架可以模仿 Louvain、ECG、Kumar 等人以及介于两者之间的任何东西，但通过超图模块化功能提供的机会得到额外增强。