目录
1.边缘检测原理
2.Sobel算子边缘检测
3.Scharr算子边缘检测
4.两种算子的生成getDerivKernels()
1.边缘检测原理
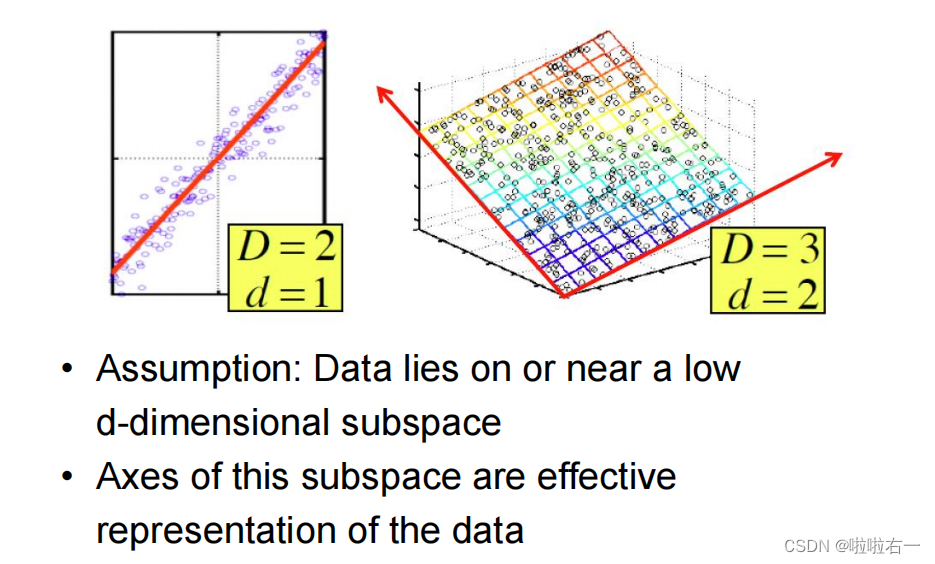
其原理是基于图像中灰度值的变化来捕捉图像中的边界和轮廓。梯度则表示了图像中像素强度变化的强弱和方向。 所以沿梯度方向找到有最大梯度值的像素,就可以获得图像中的边缘信息。

2.Sobel算子边缘检测
原理:
Sobel算子是一种常用的边缘检测算子,它可以通过计算图像的梯度来捕捉图像中的边缘信息。它分别计算图像在x和y方向上的导数,然后根据导数的值确定边缘的位置和强度。
具体来说,Sobel算子可以通过一个3x3的卷积核在图像上进行卷积操作。有两个Sobel卷积核,一个用于水平方向(x方向)的边缘检测,另一个用于垂直方向(y方向)的边缘检测。这两个卷积核分别如下:

对于输入图像中的每个像素,Sobel算子将使用这些卷积核计算其水平和垂直方向上的梯度。然后,通过对梯度的幅度进行合并,可以计算出每个像素的总梯度大小。总梯度大小表示像素点周围灰度值的变化强度,较大的变化强度通常对应于图像中的边缘。
函数:
cv::Sobel()函数将Sobel算子应用于输入图像进行卷积操作。
函数的原型如下:
CV_EXPORTS_W void Sobel( InputArray src, OutputArray dst, int ddepth,
int dx, int dy, int ksize = 3,
double scale = 1, double delta = 0,
int borderType = BORDER_DEFAULT );
下面是参数的详细解释:
-
src:输入图像,可以是单通道灰度图像或多通道图像。
-
dst:输出图像,与输入图像具有相同的尺寸和类型。
-
ddepth:输出图像的数据类型,它可以是负值(如-1)表示与输入图像保持一致,也可以是CV_8U、CV_16U、CV_32F等值,表示输出图像的深度。
-
dx和dy:分别表示在x和y方向上的导数阶数。可选值为0、1和2。
-
ksize:Sobel内核的大小,必须为1、3、5或7。值越大,滤波器的响应越平缓。
-
scale:可选的缩放因子,用于调整输出图像的值域范围。默认为1。
-
delta:可选的指定delta值,用于调整输出图像的亮度。默认为0。
-
borderType:可选的边界扩充方法,用于处理邻域超出图像边界的情况。默认为cv::BORDER_DEFAULT。
示例代码:
void Sobel_f(Mat image){
Mat gray;
cvtColor(image,gray,COLOR_BGR2GRAY);
Mat resultX,resultY,resultXY;
//X方向一阶边缘
Sobel(gray,resultX,CV_16S,1,0,1);
convertScaleAbs(resultX,resultX);
//Y方向一阶边缘
Sobel(gray,resultY,CV_16S,0,1,3);
convertScaleAbs(resultY,resultY);
//整幅图像的一阶边缘
resultXY=resultX+resultY;
//显示图像
imwrite("/sdcard/DCIM/resultX.png",resultX);
imwrite("/sdcard/DCIM/resultY.png",resultY);
imwrite("/sdcard/DCIM/resultXY.png",resultXY);
}


(X方向) ( Y方向) ( XY方向)
3.Scharr算子边缘检测
原理:
Scharr算子是一种边缘检测算子,它是Sobel算子的改进版本。Scharr算子采用了更加精确的权重分配,可以提供更好的边缘检测性能。
Scharr算子也是通过卷积操作来计算图像的梯度,类似于Sobel算子。它包含两个卷积核,一个用于水平方向(x方向)的边缘检测,另一个用于垂直方向(y方向)的边缘检测。

Scharr算子的差异在于卷积核中的权重分配相对于Sobel算子更加平衡,以提高对边缘信号的敏感度。这种平衡权重的分配可以产生更加准确的梯度估计。
Scharr算子使用相同的原理来计算像素点周围的梯度大小和方向。通过在x和y方向上对梯度进行计算,并根据梯度的幅度和方向确定边缘的位置和强度。
函数:
cv::Scharr()函数是OpenCV中的一个函数,用于计算图像的Scharr导数。它类似于Sobel算子,但是使用了更准确的权重分配。
函数原型:
CV_EXPORTS_W void Scharr( InputArray src, OutputArray dst, int ddepth,
int dx, int dy, double scale = 1, double delta = 0,
int borderType = BORDER_DEFAULT );
下面是参数的详细解释:
-
src:输入图像,可以是单通道灰度图像或多通道图像。
-
dst:输出图像,与输入图像具有相同的尺寸和类型。
-
ddepth:输出图像的数据类型,可以是负值(如-1),表示与输入图像保持一致,也可以是CV_8U、CV_16U、CV_32F等值,表示输出图像的深度。
-
dx和dy:分别表示在x和y方向上的导数阶数。可选值为0、1和2。
-
scale:可选的缩放因子,用于调整输出图像的值域范围。默认为1。
-
delta:可选的指定delta值,用于调整输出图像的亮度。默认为0。
-
borderType:可选的边界扩充方法,用于处理邻域超出图像边界的情况。默认为cv::BORDER_DEFAULT。
示例代码:
void Scharr_f(Mat img) {
Mat image;
cvtColor(img,image,COLOR_BGR2GRAY);
cv::Mat grad_x, grad_y; // 存放Scharr滤波器的梯度
cv::Mat abs_grad_x, abs_grad_y; // 存放梯度的绝对值
// 计算X方向的Scharr滤波器
cv::Scharr(image, grad_x, CV_16S, 1, 0);
cv::convertScaleAbs(grad_x, abs_grad_x);
// 计算Y方向的Scharr滤波器
cv::Scharr(image, grad_y, CV_16S, 0, 1);
cv::convertScaleAbs(grad_y, abs_grad_y);
// 合并X和Y方向的梯度
cv::Mat grad;
cv::addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad);
// 显示结果
imwrite("/sdcard/DCIM/grad.png",grad);
}
结果: (grad)
(grad)
4.两种算子的生成getDerivKernels()
getDerivKernels()函数是OpenCV中用于生成一维卷积核的函数,可用于计算图像的一阶导数。
函数的原型如下:
void cv::getDerivKernels ( OutputArray kx,
OutputArray ky,
int dx,
int dy,
int ksize,
bool normalize =false,
int ktype = CV_32F
)
- kx:行滤波器系数的输出矩阵,尺寸为ksize*1
- ky:列滤波器系数的输出矩阵,尺寸为ksize*1。
- dx:X方向导数的阶次。
- dy:Y方向导数的阶次
- ksize:滤波器的大小,可以选择的参数为FILTER SCHARR,1.35或7。
- normalize: 是否对滤波器系数进行归一化的标志,默认值为false,表示不进行系数归一化。
- ktype:滤波器系数类型,可以选择CV 32F或CV 64F,默认参数为CV 32F。
示例代码:
以下是一个使用使用getDerivKernels()函数来生成Sobel和Scharr算子卷积核的示例:
//生成边缘检测器
void f(){
cv::Mat sobel_xl, sobel_yl; // 存放分离的Sobel算子
cv::Mat scharr_x, scharr_y; // 存放分离的Scharr算子
cv::Mat sobelXl, scharrX; // 存放最终算子
// 一阶X方向Sobel算子
cv::getDerivKernels(sobel_xl, sobel_yl, 1, 0, 3);
sobel_xl = sobel_xl.reshape(1, 1); // 转换为单行矩阵
sobelXl = sobel_yl * sobel_xl; // 计算滤波器
// X方向Scharr算子
cv::getDerivKernels(scharr_x, scharr_y, 1, 0, cv::FILTER_SCHARR);
scharr_x = scharr_x.reshape(1, 1); // 转换为单行矩阵
scharrX = scharr_y*scharr_x; // 计算滤波器
ostringstream ss;
// 打印生成的卷积核
ss<< "Sobel X方向卷积核:" << sobelXl << endl;
ss << "Scharr X方向卷积核:" << scharrX <<endl;
LOGD("%s",ss.str().c_str());
}我们使用getDerivKernels()函数生成了X方向Sobel算子和X方向Scharr算子的卷积核。然后,我们将其转换为单行矩阵,并通过乘法运算计算得到滤波器。