❓ 剑指 Offer 46. 把数字翻译成字符串
难度:中等
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
示例 1:
输入: 12258
输出: 5
解释: 12258有5种不同的翻译,分别是"bccfi", “bwfi”, “bczi”, “mcfi"和"mzi”
提示:
- 0 < = n u m < 2 31 0 <= num < 2^{31} 0<=num<231
💡思路:动态规划
定义 dp 数组,dp[i] 表示以第 i 个字符结尾的子串的 总 翻译方法;
如果 若
x
i
x_i
xi 和
x
i
−
1
x_{i-1}
xi−1 组成的两位数字可以被翻译,则 dp[i]=dp[i−1]+dp[i−2];否则 dp[i]=dp[i−1]。
- 可被翻译的两位数区间:当
x
i
−
1
=
0
x_{i-1} = 0
xi−1=0 时,组成的两位数是无法被翻译的(例如
00,01,02,⋯),因此区间为[10,25]。 - 所以状态转移方程为: d p [ i ] = { d p [ i − 1 ] + d p [ i − 2 ] , 10 x i − 1 + x i ∈ [ 10 , 25 ] d p [ i − 1 ] , 10 x i − 1 + x i ∈ [ 0 , 10 ) ∪ ( 25 , 99 ] dp[i]=\begin{cases}dp[i-1]+dp[i-2]&,10x_{i-1}+x_i\in[10,25]\\dp[i-1]&,10x_{i-1}+x_i\in[0,10)\cup(25,99]\end{cases} dp[i]={dp[i−1]+dp[i−2]dp[i−1],10xi−1+xi∈[10,25],10xi−1+xi∈[0,10)∪(25,99]
观察上面的 状态转移方程,发现 dp[i] 只与 前两位 dp[i - 1]、 dp[i - 2] 有关,所以可以进行空间优化,我们使用 pre1 代替 dp[i - 1], pre2 代替 dp[i - 2],cur 代替 dp[i]:
c
u
r
=
{
p
r
e
1
+
p
r
e
2
,
10
x
i
−
1
+
x
i
∈
[
10
,
25
]
p
r
e
1
,
10
x
i
−
1
+
x
i
∈
[
0
,
10
)
∪
(
25
,
99
]
cur=\begin{cases}pre1+pre2&,10x_{i-1}+x_i\in[10,25]\\pre1&,10x_{i-1}+x_i\in[0,10)\cup(25,99]\end{cases}
cur={pre1+pre2pre1,10xi−1+xi∈[10,25],10xi−1+xi∈[0,10)∪(25,99]
-
当前 状态
cur处理完,pre和pre2共同前移一位,进而可以表示为:
p r e 1 = { p r e 1 + p r e 2 , 10 x i − 1 + x i ∈ [ 10 , 25 ] p r e 1 , 10 x i − 1 + x i ∈ [ 0 , 10 ) ∪ ( 25 , 99 ] pre1=\begin{cases}pre1+pre2&,10x_{i-1}+x_i\in[10,25]\\pre1&,10x_{i-1}+x_i\in[0,10)\cup(25,99]\end{cases} pre1={pre1+pre2pre1,10xi−1+xi∈[10,25],10xi−1+xi∈[0,10)∪(25,99]
p r e 2 = { p r e 1 − p r e 2 , 10 x i − 1 + x i ∈ [ 10 , 25 ] p r e 1 , 10 x i − 1 + x i ∈ [ 0 , 10 ) ∪ ( 25 , 99 ] pre2=\begin{cases}pre1-pre2&,10x_{i-1}+x_i\in[10,25]\\pre1&,10x_{i-1}+x_i\in[0,10)\cup(25,99]\end{cases} pre2={pre1−pre2pre1,10xi−1+xi∈[10,25],10xi−1+xi∈[0,10)∪(25,99] -
按位遍历该数字,从
左到右和右到左是相同的,本方法使用右到左。 -
初始化:
pre1 = pre2 = 1,即 “无数字” 和 “第 1 位数字” 的翻译方法数量均为1。
🍁代码:(C++、Java)
C++
class Solution {
public:
int translateNum(int num) {
if(num < 10) return 1;
int pre1 = 1, pre2 = 1;
while(num >= 10){
int tmp = num % 100;
if(tmp / 10 > 0 && tmp <= 25) {
pre1 += pre2;
pre2 = pre1 - pre2;
}else{
pre2 = pre1;
}
num /= 10;
}
return pre1;
}
};
Java
class Solution {
public int translateNum(int num) {
if(num < 10) return 1;
int pre1 = 1, pre2 = 1;
while(num >= 10){
int tmp = num % 100;
if(tmp / 10 > 0 && tmp <= 25) {
pre1 += pre2;
pre2 = pre1 - pre2;
}else{
pre2 = pre1;
}
num /= 10;
}
return pre1;
}
}
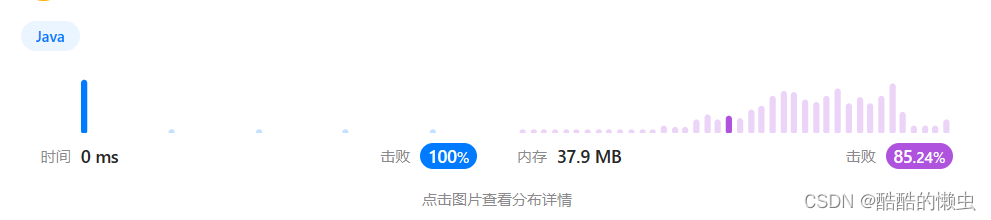
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度:
O
(
n
)
O(n)
O(n),其中
n为字符串s的长度。 - 空间复杂度: O ( 1 ) O(1) O(1),使用常数大小的额外空间。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!