超图聚类论文阅读1:Kumar算法
《超图中模块化的新度量:有效聚类的理论见解和启示》
《A New Measure of Modularity in Hypergraphs: Theoretical Insights and Implications for Effective Clustering》
COMPLEX NETWORKS 2020, SCI 3区
具体实现源码见HyperNetX库
工作:
- 针对超图聚类问题推广了模块度最大化框架
- 引入了一个超图空模型,它与无向图的配置模型完全对应。
- 推导出一个保留超图节点度序列的邻接矩阵缩减
成果:
- 使用 Louvain 方法最大化由此产生的模块化函数,已知在图实践中效果很好
- 在几个真实世界的数据集上展示了我们的方法的有效性
简介
先前工作
-
注意力限制在 k-均匀超图上,其中所有超边具有相同的固定大小。
提出合适的超图拉普拉斯算子来扩展一般超图的谱聚类框架——隐含了图扩展的思想
-
模块度最大化是图上聚类的另一种方法,它提供了一个标准来衡量模块化函数中的集群质量
经典方法为louvain算法
-
团扩展问题:会丢失编码在超边结构中的关键信息。也不会保留超图的节点度——这是模块度最大化方法基于的零模型所必需的
-
有多种切割超边的方法。根据切割不同侧节点的比例和分配,聚类将发生变化。需要考虑超边权重
本文贡献
- 在超图上定义了一个空模型(可以保持超图节点度信息),并使用上述定义了一个模块化函数,可以使用 Louvain 方法将其最大化。
- 提出了一种迭代超边重新加权过程,该过程利用来自超图结构的信息和超边切割的平衡。
- 在几个真实世界的数据集上凭经验评估了生成的算法,证明了其相对于竞争基线的有效性和效率。
背景知识
- 超图——关联矩阵、团扩展
- 模块度
超图模块度
节点的采样概率与其参与的超边的数量(或在加权情况下,总权重)成正比
P
i
j
h
y
p
=
d
(
i
)
×
d
(
j
)
∑
v
∈
V
d
(
v
)
P_{i j}^{h y p}=\frac{d(i) \times d(j)}{\sum_{v \in V} d(v)}
Pijhyp=∑v∈Vd(v)d(i)×d(j)
- 在进行团扩展时,相应图中节点的度数与它在图中的度数不同原始超图
对于每个超边 e,节点度被多算了一个因子 (δ(e) − 1)。因此,我们可以通过将每个 w(e) 缩小一个因子 (δ(e) − 1) 来纠正它。这导致以下更正的邻接矩阵:
A
h
y
p
=
H
W
(
D
e
−
I
)
−
1
H
T
A^{h y p}=H W\left(D_e-I\right)^{-1} H^T
Ahyp=HW(De−I)−1HT
我们可以使用这种保留节点度数的缩减,将对角线归零,以实现方程式中的空模型。
超图模块度的表达式:
Q
h
y
p
=
1
2
m
∑
i
j
[
A
i
j
h
y
p
−
P
i
j
h
y
p
]
δ
(
g
i
,
g
j
)
Q^{h y p}=\frac{1}{2 m} \sum_{i j}\left[A_{i j}^{h y p}-P_{i j}^{h y p}\right] \delta\left(g_i, g_j\right)
Qhyp=2m1ij∑[Aijhyp−Pijhyp]δ(gi,gj)
与任何加权图一样,此函数的范围是 [−1, 1]。当超边中没有一对节点属于同一集群时,我们将得到 Qhyp = −1,而当属于同一超边的任何两个节点始终属于同一集群时,我们将得到 Qhyp = 1。 Qhyp = 0,对于任何一对节点 i 和 j,同时包含 i 和 j 的超边数等于包含 i 和 j 的随机连线超边数,由空模型给出。
迭代超边重新加权
问题:最小切割算法会支持尽可能不平衡的切割
思路:我们希望在簇中保留不平衡的超边,并切割更平衡的超边——可以通过增加获得不平衡切割的超边的权重,并减少获得更平衡切割的超边的权重来完成。
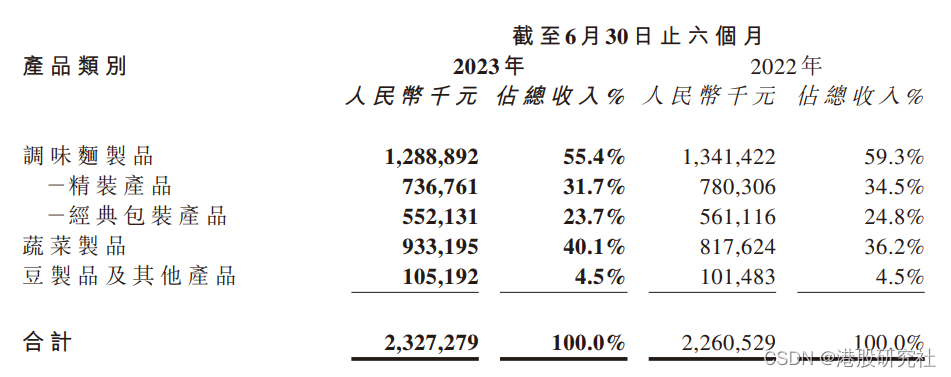
超边被一分为二,两边节点数分别为k1、k2:
t
=
(
1
k
1
+
1
k
2
)
×
δ
(
e
)
t=\left(\frac{1}{k_1}+\frac{1}{k_2}\right) \times \delta(e)
t=(k11+k21)×δ(e)
当
k
1
=
k
2
=
δ
(
e
)
/
2
k1=k2=\delta(e)/2
k1=k2=δ(e)/2时,t取最小值4,推广上式:
w
′
(
e
)
=
1
m
∑
i
=
1
c
1
k
i
+
1
[
δ
(
e
)
+
c
]
w^{\prime}(e)=\frac{1}{m} \sum_{i=1}^c \frac{1}{k_i+1}[\delta(e)+c]
w′(e)=m1i=1∑cki+11[δ(e)+c]
——+1 和 +c 项都被添加用于平滑,以解决任何 ki 为零的情况。我们除以 m 来归一化权重
令 wt(e) 为超边 e 在第 t 次迭代中的权重,w’(e) 为在给定迭代中计算的权重,则权重更新规则可写为:
w
t
+
1
(
e
)
=
α
w
t
(
e
)
+
(
1
−
α
)
w
′
(
e
)
w_{t+1}(e)=\alpha w_t(e)+(1-\alpha) w^{\prime}(e)
wt+1(e)=αwt(e)+(1−α)w′(e)
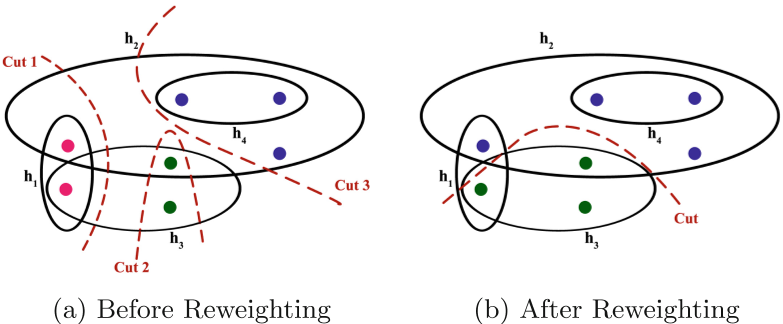
示例
初始的切分很不均匀,有1:4、1:2、2:3等切分,改进后,不均匀的切割被去除——h1 和 h3 中的单个节点最初分配给另一个集群,已被拉回它们各自的(更大的)集群。
实验
度量指标:
- 使用平均 F1 度量 和兰德指数RI来评估具有真实类别标签的真实世界数据的聚类性能
几种用作对比的方法:
-
团扩展+louvain
-
超图谱聚类
-
hMETIS 和 PaToH
数据集:
- MovieLens:联合导演
- Cora 和 Citeseer:论文共同作者
- TwitterFootball:足球俱乐部
- Arnetminer:共引论文
结果:
- 在所有数据集上显示最佳平均 F1 分数、在除一个数据集外的所有数据集上显示最佳兰德指数分数
- 在所有数据集和两种实验设置上都优于各自的团扩展方法
- f分析得出碎片边增加,这可能对应于更平衡的切割
结论
- 考虑了超图上的模块化最大化问题。在提出超图的模块化函数时,我们推导出了一个节点度保持图缩减和一个超图空模型
- 为了进一步细化聚类,我们提出了一种超边重新加权过程,可以平衡聚类方法引起的切割
- 迭代重新加权模块化最大化 (IRMM)在数据集上表现出不错的性能