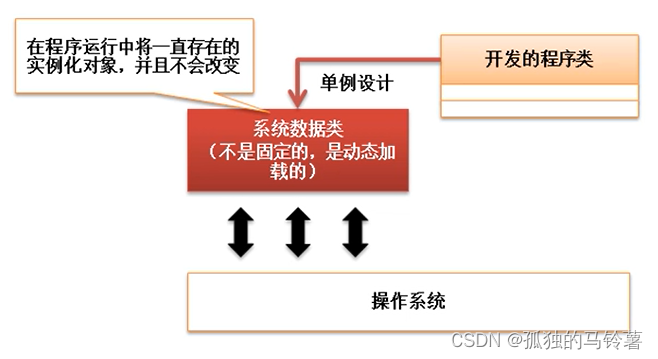
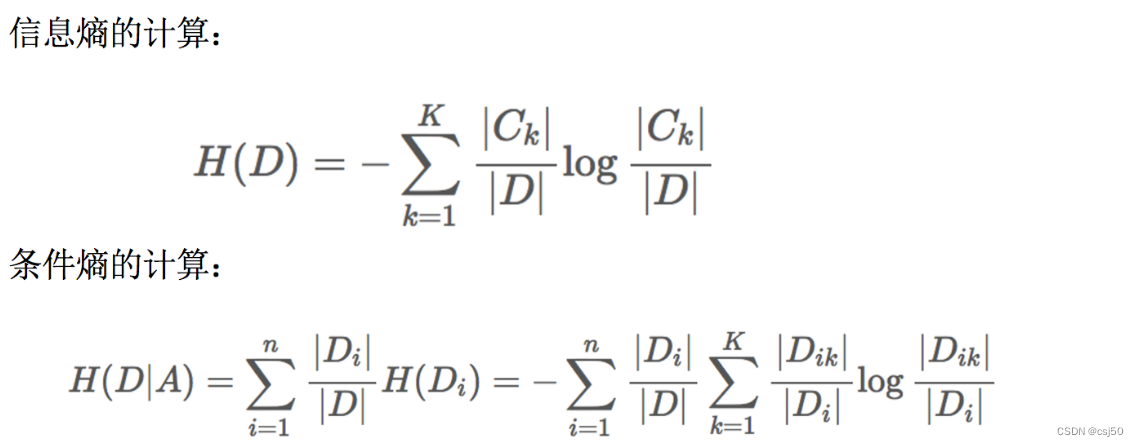一、决策树

1、认识决策树
决策树思想的来源非常朴素，程序设计中的条件分支结构就是if-else结构，最早的决策树就是利用这类结构分割数据的一种分类学习方法

2、一个对话的例子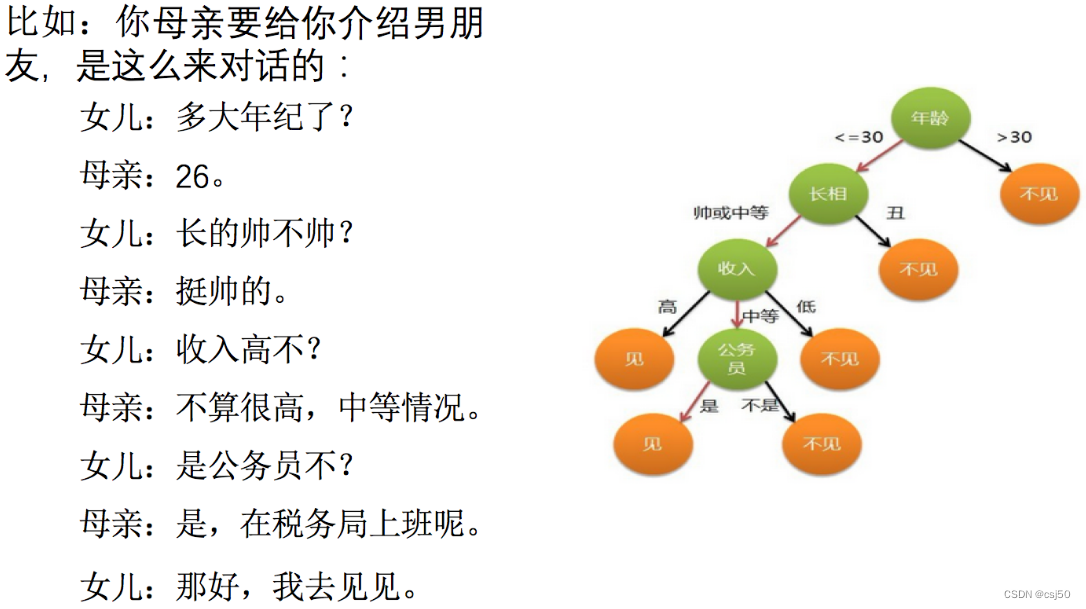

想一想这个女生为什么把年龄放在最上面判断！！！
如何高效的进行决策？特征的先后顺序

二、决策树分类原理详解

1、我们通过一个问题例子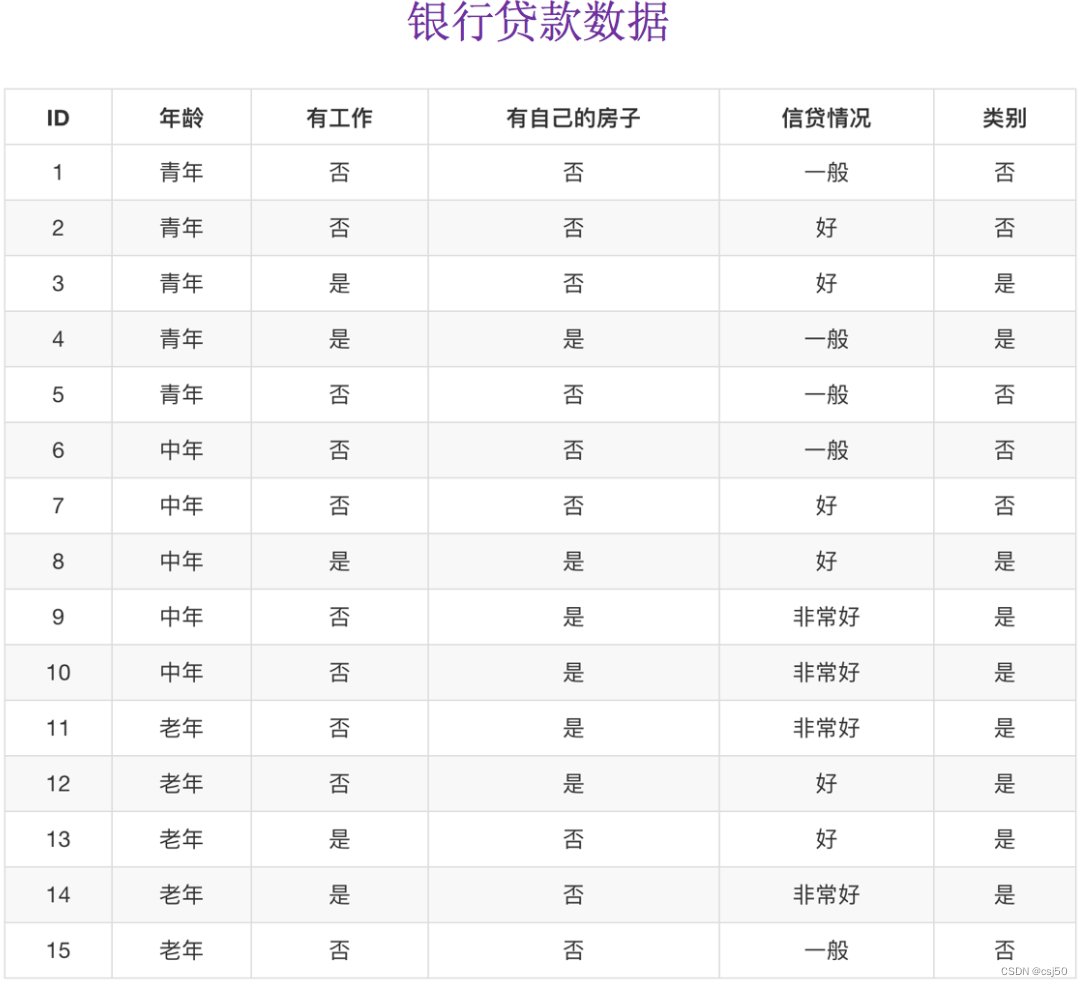

已知有四个特征值，预测是否贷款给某个人
（1）先看房子，再看工作 --> 是否贷款（只看了两个特征）
（2）年龄，信贷情况，工作 --> 看了三个特征
第二种这种方式就没有第一种高效
希望能够找到一种数学的方法，快速自动的判断，应该先看哪个特征

2、信息论基础
需要引入信息熵、信息增益等信息论的知识！！！

（1）信息
香农定义的：消除随机不定性的东西
小明 年龄 "我今年18岁"
小华 "小明明年19岁"

小明说了之后，小华说的这句话就变成废话了，不是信息

（2）信息的衡量 -- 信息量 -- 信息熵

3、信息熵的定义
H的专业术语称之为信息熵，单位为比特bit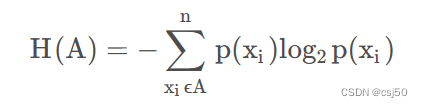

4、以银行贷款数据为例，计算信息熵
某人，已知年龄、工作、房子、信贷情况，是否贷款给这个人？
需要衡量不确定性的大小
这里有两种情况，一种是贷款，一种是不贷款
不贷款的概率是6/15，贷款的概率是9/15
H(总) = -(6/15 * log 6/15 + 9/15 * log 9/15) = 0.971

当我们知道某一个特征之后，不确定性会减少
那么我们如果能求出，知道某个特征之后，不确定性减少的程度。再比较，知道哪一个特征之后，不确定性减少的程度是最多的。我们是不是可以先看这个特征

求当知道某个特征之后，它的信息熵是多少？
引入—信息增益

5、信息增益
决策树的划分依据之一—信息增益

（1）定义和公式
特征A对训练数据集D的信息增益g(D,A)，定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差
g(D,A) = H(D) - 条件熵H(D|A)
信息增益就衡量了，知道某个特征之后，它的不确定性的减少程度

计算知道年龄之后的信息增益是多少：
g(D,年龄) = H(D) - H(D|年龄)

求H(D|年龄)：
H(青年) = -(2/5 * log 2/5 + 3/5 * log 3/5) = 
H(中年) = -(2/5 * log 2/5 + 3/5 * log 3/5) = 
H(老年) = -(1/5 * log 1/5 + 4/5 * log 4/5) = 
H(D|年龄) = 1/3 * H(青年) + 1/3 * H(中年) + 1/3 * H(老年)

我们以A1、A2、A3、A4代表年龄、有工作、有自己的房子和贷款情况。最终计算的结果g(D, A1) = 0.313, g(D, A2) = 0.324, g(D, A3) = 0.420,g(D, A4) = 0.363。所以我们选择A3作为划分的第一个特征

（2）公式