1.1栈的定义
栈(stack)是一种只能在一端进行插入或删除的线性表
下面是一些基础概念
- 栈顶(top) : 表中允许进行插入、删除操作的线性表
- 栈底(bottom):表的另一端
- 空栈 :栈中没有数据元素
- 进栈/入栈(push):栈的插入操作
- 出栈/退栈(pop):栈的删除操作
栈的抽象数据类型定义:

1.2栈的存储结构
采用顺序存储结构的栈称为顺序栈
栈中的元素相对位置是成线性的
声明:
typedef char ElemType;
typedef struct
{
ElemType data[MaxSize];
int top; //栈顶指针
}SqStack;
图示:

1.3 顺序栈基本运算
我们首先要明确几点:
- 栈满的条件:s–>top = MaxSize - 1
- 元素e的进栈操作:先将栈顶指针top增1,然后将元素e放在栈顶指针处
- 出栈操作:先将栈顶指针top处的元素取出放在e中,然后栈顶指针减1
操作图示:
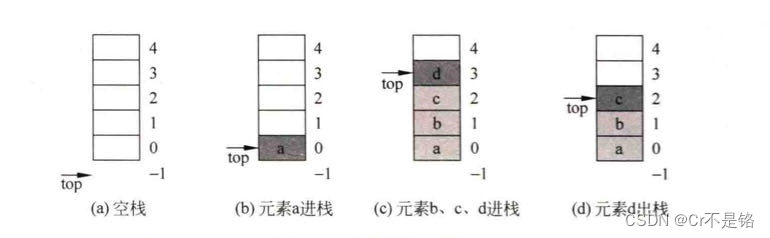
(1)初始化栈
//栈的初始化
void InitStack(SqStack*& s)
{
s = (SqStack*)malloc(sizeof(SqStack));
s->top = -1;//栈顶指针置-1
}
(2)销毁栈
//栈的销毁
void DestroyStack(SqStack*& s)
{
free(s);
}
(3)判断栈是否为空
//栈是否为空
bool StackEmpty(SqStack* s)
{
return (s->top == -1);
}
(4)进栈
//进栈
bool Push(SqStack*& s, ElemType e)
{
if (s->top == MaxSize -1)//栈满
return false;
s->top++; //栈顶指针增一
s->data[s->top] = e; //元素e放在栈顶指针处
return true;
}
(5)出栈
bool Pop(SqStack*& s, ElemType& e)
{
if (s->top == -1)
return false;
e = s->data[s->top];//取栈顶元素
s->top--;
return true;
}
(6)取栈顶元素
bool GetTop(SqStack* s, ElemType& e)
{
if (s->top == -1)
return false;
e = s->data[s->top];
return true;
}
顺序栈的完整代码如下:
#include<iostream>
using namespace std;
#define MaxSize 50
typedef char ElemType;
typedef struct
{
ElemType data[MaxSize];
int top; //栈顶指针
}SqStack;
//栈的初始化
void InitStack(SqStack*& s)
{
s = (SqStack*)malloc(sizeof(SqStack));
s->top = -1;//栈顶指针置-1
}
//栈的销毁
void DestroyStack(SqStack*& s)
{
free(s);
}
//栈是否为空
bool StackEmpty(SqStack* s)
{
return (s->top == -1);
}
//进栈
bool Push(SqStack*& s, ElemType e)
{
if (s->top == MaxSize -1)//栈满
return false;
s->top++; //栈顶指针增一
s->data[s->top] = e; //元素e放在栈顶指针处
return true;
}
bool Pop(SqStack*& s, ElemType& e)
{
if (s->top == -1)
return false;
e = s->data[s->top];//取栈顶元素
s->top--;
return true;
}
bool GetTop(SqStack* s, ElemType& e)
{
if (s->top == -1)
return false;
e = s->data[s->top];
return true;
}
int main() {
SqStack* st;
ElemType e;
ElemType s[] = "abcba";
return 0;
}
1.3栈的链式存储结构
由于栈中的数据元素的逻辑关系呈线性关系,所以栈可以像顺序表由于采用链式存储结构。即链栈
优点:相比于顺序栈,在内存允许情况下,链栈是不存在栈满的情况。
声明如下:
typedef char ElemType;
typedef struct linknode
{
ElemType data; //数据域
struct linknode* next;//指针域
}LinkStNode;
1.4链栈的基本算法
重点:
- 栈空的条件:s–>next == NULL
- 元素e进栈操作:新建一个结点存放元素e,将结点p插入到头结点之后
- 出栈操作:取出首结点的data值并将其删除
(1)初始化栈
//初始化栈
void InitStack(LinkStNode*& s)
{
s = (LinkStNode*)malloc(sizeof(LinkStNode));
s->next = NULL;
}
(2)销毁栈
//销毁栈
void DestroyStack(LinkStNode*& s)
{
LinkStNode* pre = s, * p = s->next;
while (p != NULL)
{
free(pre);
pre = p;
p = pre->next;
}
free(pre);
}
(3)判断栈为空
//判断栈是否为空
bool StackEmpty(LinkStNode* s)
{
return (s->next == NULL);
}
(4)进栈
//进栈
void Push(LinkStNode*& s, ElemType e)
{
LinkStNode* p;
p = (LinkStNode*)malloc(sizeof(LinkStNode));//不要忘记开辟空间
p->data = e;
p->next = s->next;
s->next = p;
}
(5)出栈
bool Pop(LinkStNode*& s, ElemType& e)
{
LinkStNode* p;
if (s->next == NULL)
return false;
p = s->next;
e = p->data;
s->next = p->next;
}
(6)取栈顶元素
bool GetTop(LinkStNode* s, ElemType& e)
{
if (s->next == NULL)
return false;
e = s->next->data;
return true;
}
完整代码:
#include<iostream>
using namespace std;
typedef char ElemType;
typedef struct linknode
{
ElemType data; //数据域
struct linknode* next;//指针域
}LinkStNode;
//初始化栈
void InitStack(LinkStNode*& s)
{
s = (LinkStNode*)malloc(sizeof(LinkStNode));
s->next = NULL;
}
//销毁栈
void DestroyStack(LinkStNode*& s)
{
LinkStNode* pre = s, * p = s->next;
while (p != NULL)
{
free(pre);
pre = p;
p = pre->next;
}
free(pre);
}
//判断栈是否为空
bool StackEmpty(LinkStNode* s)
{
return (s->next == NULL);
}
//进栈
void Push(LinkStNode*& s, ElemType e)
{
LinkStNode* p;
p = (LinkStNode*)malloc(sizeof(LinkStNode));//不要忘记开辟空间
p->data = e;
p->next = s->next;
s->next = p;
}
//出栈
bool Pop(LinkStNode*& s, ElemType& e)
{
LinkStNode* p;
if (s->next == NULL)
return false;
p = s->next;
e = p->data;
s->next = p->next;
}
//取栈顶元素
bool GetTop(LinkStNode* s, ElemType& e)
{
if (s->next == NULL)
return false;
e = s->next->data;
return true;
}
}
int main()
{
ElemType chs1[] = "(())";
ElemType chs2[] = "(()))";
return 0;
}
希望本文能对你有所帮助!

`