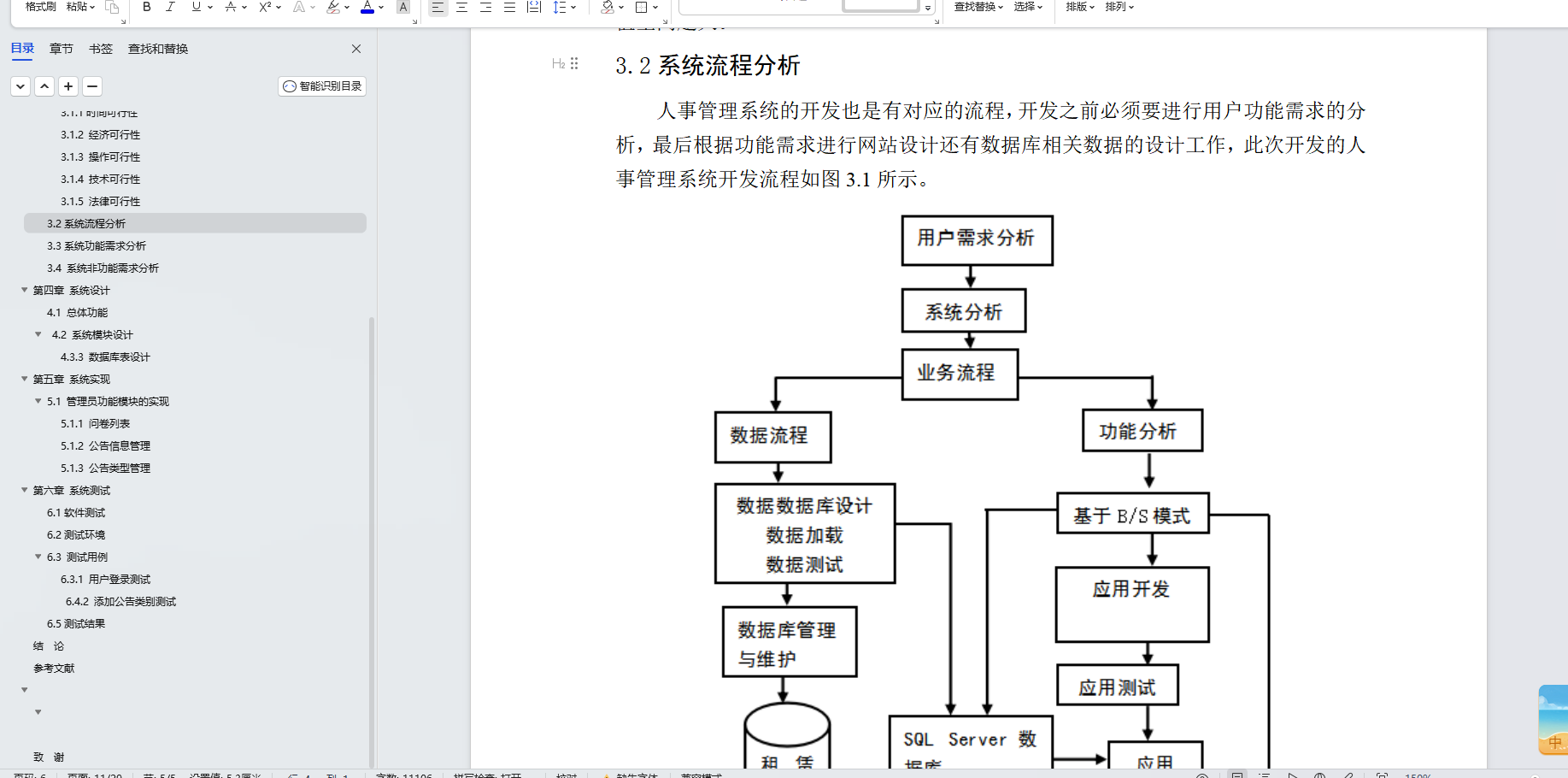
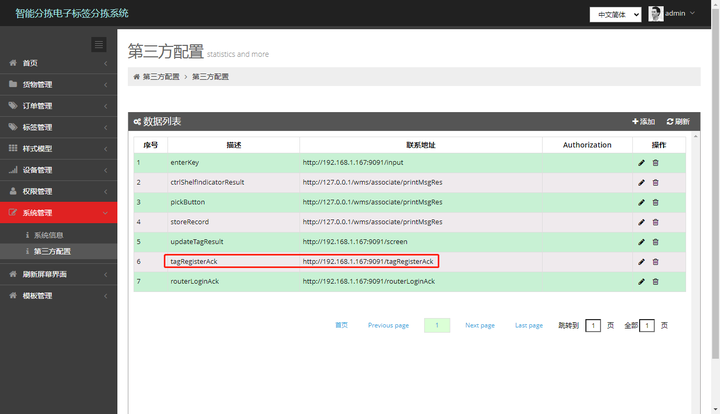
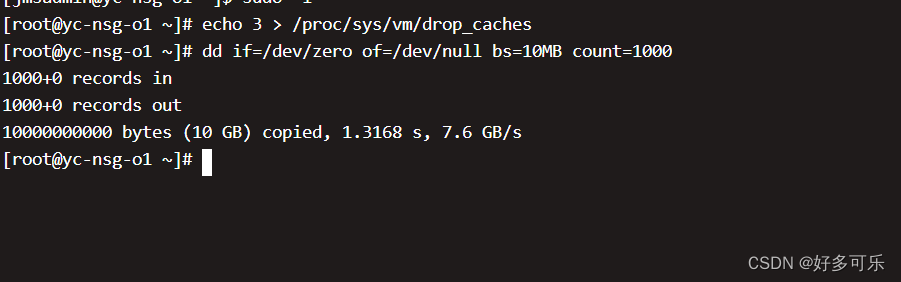
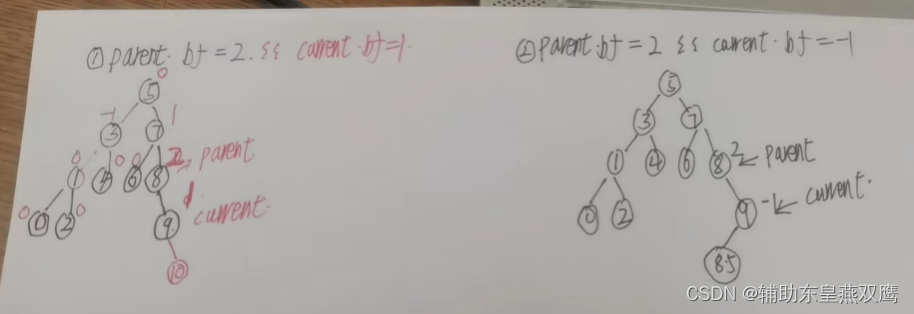高阶数据结构-----三种平衡树的实现以及原理(未完成)

news2024/10/2 22:26:12

TreeMap和TreeSet的底层实现原理就是红黑树

一)AVL树:

1)必须是一棵搜索树:前提是二叉树，任取一个节点，它的左孩子的Key小于父亲节点的Key小于右孩子节点的Key，中序遍历是有序的，按照Key的大小进行排列，高度平衡的二叉搜索树，他的左右子树都是二叉搜索树
          A
    B             C
甲    乙      丙      丁
我们在这里面得出一个结论: Key(甲)<Key(B)<Key(乙)<Key(A)<Key(丙)<Key(C)<Key(丁)

2)必须是一颗平衡树:任意树中的节点，要求结点左子树的高度和结点右子树的高度差的绝对值不可以超过1，左右子树的高度差不能超过1；

平衡因子=左子树的高度-右子树的高度，我们在AVL树中任取一个节点，他的平衡因子只能是-1，1，0；

3)AVL树任意一颗以根节点的左右子树的高度差的绝对值不超过1，所以AVL树尽量保证左树和右树的高度是一致的，那么这个时候再次进行数据查找的时间复杂度就是O(logN)

4)当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过，(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度

二)AVL树的查找与插入:如果插入失败了，那么只有一种情况那么就是当前我要插入的数值在原来的树中已经有了

随着节点的插入，导致了平衡因子发生了变化，所以我们要进行平衡因子的调节

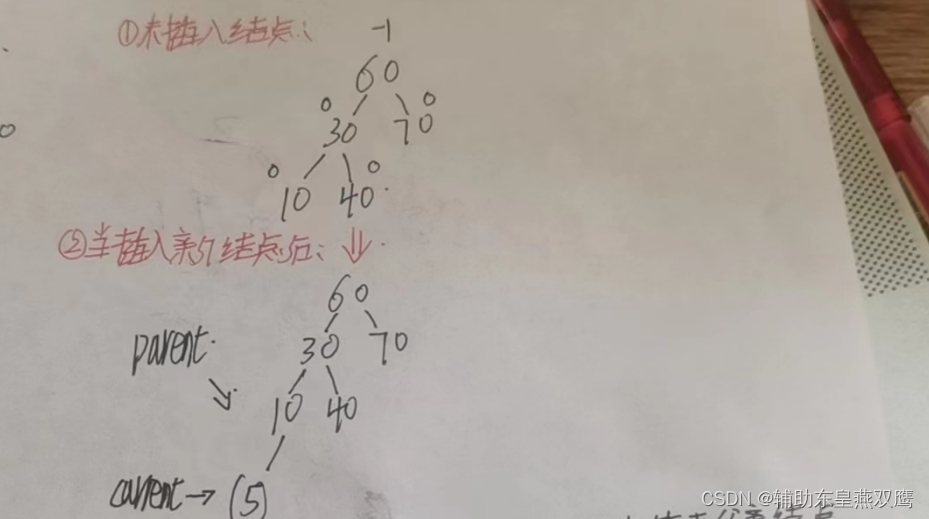
1)如图所示，在上面这张图中当我们想要插入10这个节点的时候，parent此时指向的是9这个节点，此时10插入到了9的右子树，那么9的平衡因子++，此时parent的平衡因子是1，但是只能证明当前这棵树已经平衡了，还是需要进行向上调整

2)此时如果插入的数据是8.5，那么此时插入到的位置是9的左边，此时parent的平衡因子是-1，此时也是只能证明当前这棵树平衡了，还是需要继续向上调整的；

3)但是如果此时我们进行插入的数据是7.5，那么此时parent节点指向8这个位置，成功插入7.5这个数据之后发现parent的平衡因子变成0，此时就不需要向上调整了

当parent.bf==2的时候，说当前这棵树已经不平衡了，说明此时右树高，说明要降低右树的高度，增加左树的高度，所以要进行旋转

当parent.bf==-2的时候，说当前这棵树已经不平衡了，说明此时左树高，说明要降低左树的高度，增加右树的高度，所以要进行旋转

左旋说明右树高，右旋说明左树高

一)parent节点的平衡因子是2，current节点存储的平衡因子是1:

二)parent结点的平衡因子是2，current的节点的平衡因子是-1;

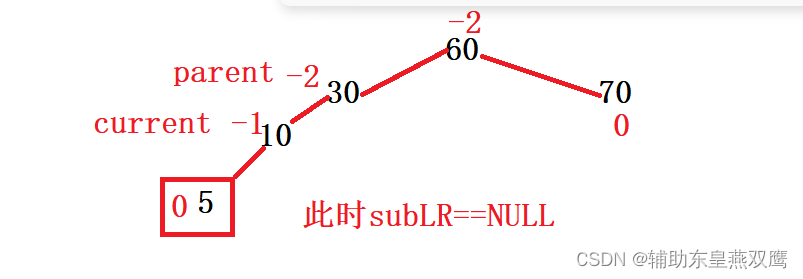
三)parent结点存储的平衡因子是-2，current存储结点的平衡因子是-1;

1)这个旋转也叫做右单旋，除了修改指针的指向还有修改平衡因子，右单旋就是自己变成左孩子的右孩子

2)但是代码写到这里面还是存在着一定问题，可能当前的parent是上面某一棵树的左子树，也有可能是某一棵树的右子树

3)最后修改各个节点的平衡因子

4)但是上面的所有情况都考虑得比较不错了，但是最终的代码还是存在着一定的瑕疵

四)parent存储结点的平衡因子是-2，current存储结点的平衡因子是1;