组合就是从m个元素的数组中求n个元素的所有组合，代码如下：

#include <iostream>
#include <vector>
using namespace std;
// 递归求解组合
void combinations(vector<int>& nums, vector<int>& combination, int start, int n, vector<vector<int>>& result) {
    if (n == 0) {
        result.push_back(combination);
        return;
    }
    for (int i = start; i < nums.size(); i++) {
        combination.push_back(nums[i]);
        combinations(nums, combination, i + 1, n - 1, result);
        combination.pop_back();
    }
}
vector<vector<int>> getCombinations(vector<int>& nums, int n) {
    vector<vector<int>> result;
    vector<int> combination;
    combinations(nums, combination, 0, n, result);
    return result;
}
int main() {
    int m, n;
    cout << "请输入元素总数m：";
    cin >> m;
    cout << "请输入需要取出的元素个数n：";
    cin >> n;
    // 生成m个元素的数组
    vector<int> nums(m);
    for (int i = 0; i < m; i++) {
        nums[i] = i + 1;
    }
    // 求解组合
    vector<vector<int>> result = getCombinations(nums, n);
    // 输出结果
    cout << "所有组合如下：" << endl;
    for (const auto& combination : result) {
        for (const auto& num : combination) {
            cout << num << " ";
        }
        cout << endl;
    }
    return 0;
}

总体流程是这样：

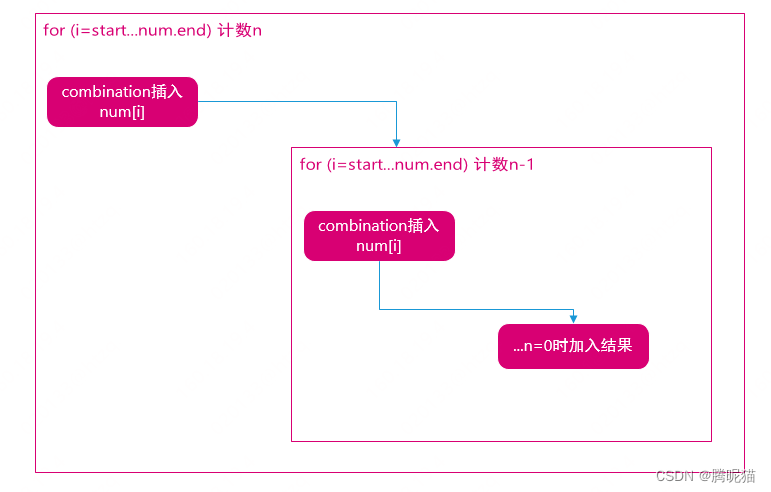
因为组合不考虑顺序，就以默认数组顺序为准，依次遍历。当前状态保存在各递归的栈中，通过循环进行推动，获得各种组合。

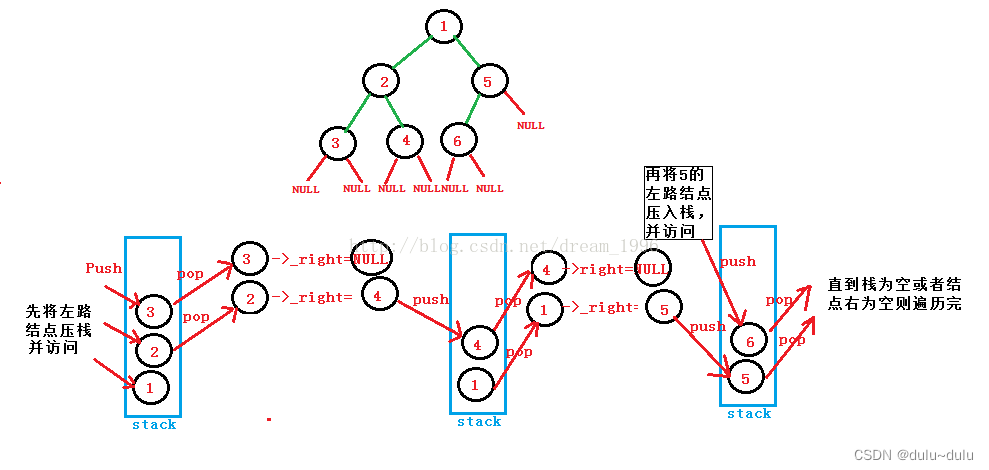
这个算法的本质实际是一种状态机的保存和状态变化，从1个数的状态到n各数的状态，然后再逐一更换n个数的值。这实际是一种树状的状态机转换，这就是这个问题看上去比较复杂的原因。如何遍历这棵树，这里使用的是深度遍历，先遍历到最末叶子节点，然后再遍历其子节点，如此循环往复。放到这个算法，状态机的推进转换实际是通过C++函数栈的形式进行保存的。我们在做这些算法题目的时候应该牢记这种栈机制。实际我们用自己创建的栈也可以同样实现，只要记录每个遍历到的节点的当前状态（循环到哪个数字）、求值域（循环到哪个数值结束）。

高清算法的最核心原理，将其关联到最基础的几个简单的认知。这样理解这些算法就很简单了。