归并排序 平均时间复杂度O(n*logn),空间复杂度O(n)

递归实现

思路：

分治法

即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。归并排序是一种稳定的排序方法

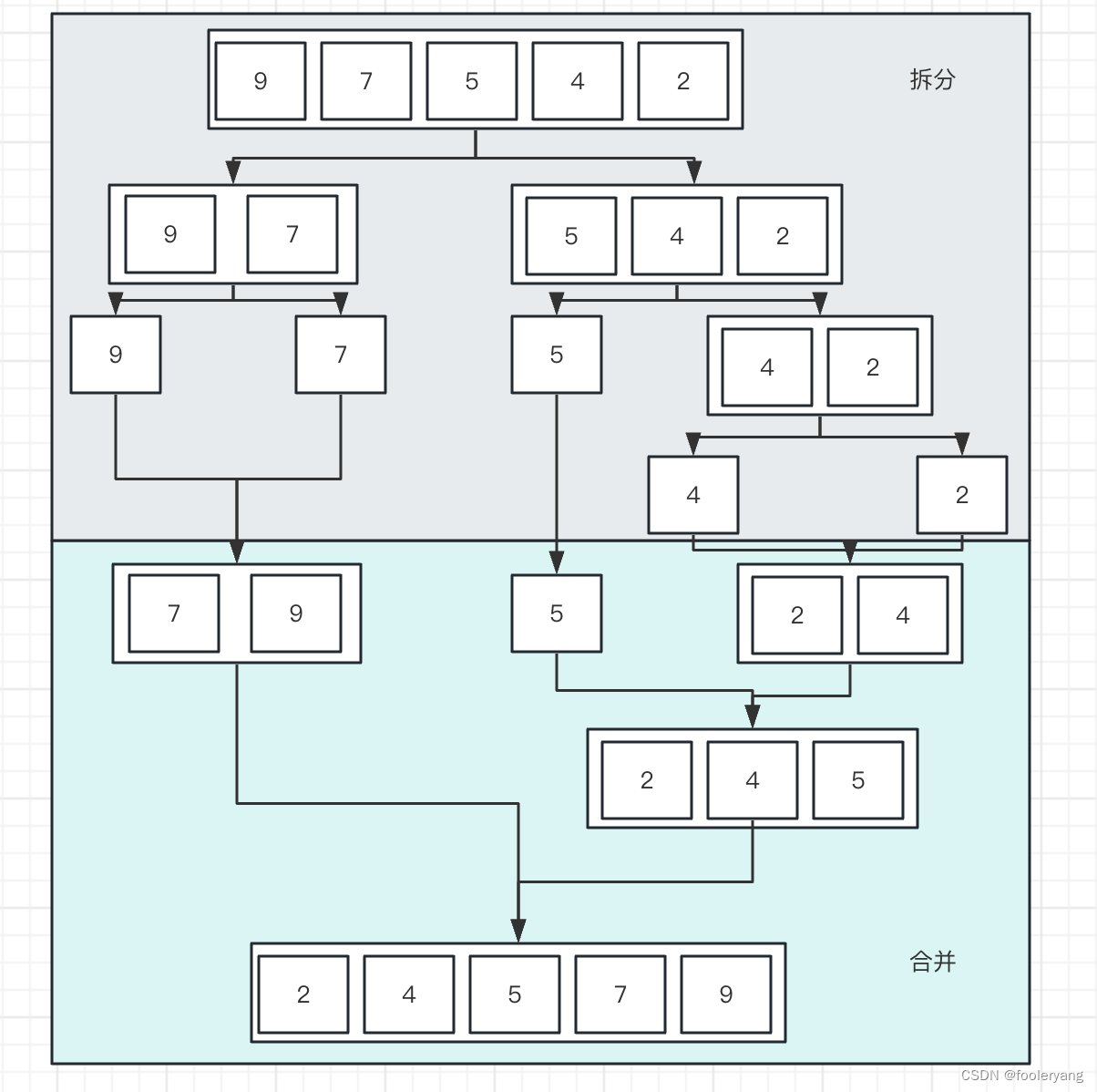
code：

    //递归版
    public static void mergetSort1(int [] arr){
        //边界判断
        if(arr == null ||arr.length < 2)
            return;
        progress(arr,0,arr.length-1);
    }

    //递归将arr[L,R]内数据排序
    //O(N*logN)
    public static void progress(int [] arr,int L,int R){
        if(L == R){
            return;
        }
        //一次性申请辅助空间
        int [] help = new int[arr.length];
        //中间位置
        int mid = L + ((R - L) >> 1);
        //将左侧排序
        progress(arr,L,mid);
        //将右侧排序
        progress(arr,mid+1,R);
        //将左右侧合并排序
        merge(arr,L,mid,R,help);
    }
    //合并排序arr[L,mid]和arr[mid+1,R]
    //申请一个辅助数组，长度位L和R的之间长度，用于保存排序后的结果
    //p1为左侧开始位，p2为右侧开始位
    //对比排序后，将剩余数记录到help中
    public static void merge(int [] arr,int L,int mid,int R,int [] help){
        int i = 0;
        //对比开始位置
        int p1 = L,p2 = mid+1;
        //对比限制
        while (p1 <= mid && p2 <= R){
            //如果arr[p1] <= arr[p2]则将arr[p1]放入help中 ,然后p1++ ,i++
            //否则 将arr[p2]放入help中，然后 p2++,i++
            help[i++] = arr[p1]<=arr[p2]?arr[p1++]:arr[p2++];
        }
        //将剩余数放入help中
        while (p1<=mid){
           help[i++] = arr[p1++];
        }
        while (p2<=R){
           help[i++] = arr[p2++];
        }
        //将help中数放到arr中
        for(i=0;i<R-L+1;i++){
           arr[L+i] = help[i];
        }
    }

非递归实现

思路：

通过步长从1->2->4->8...拆分数组，每一次合并排序有序子数组

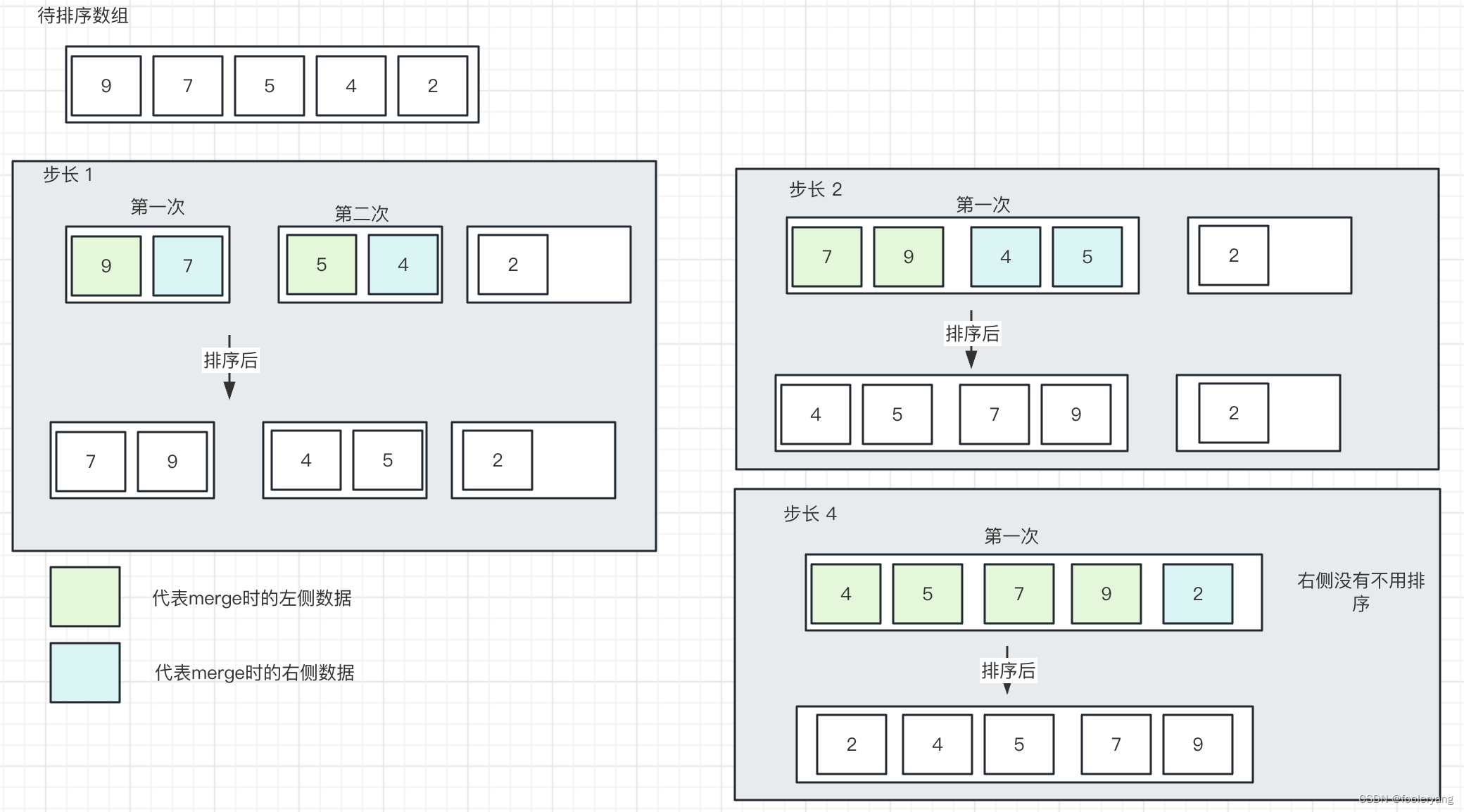
code:

    //非递归 归并排序
    //步长从 1 ->2 ->4 ->8
    //分别对步长内左右进行排序
    public static void mergeSort2(int [] arr){
        if(arr == null || arr.length <2)
            return;

        //步长
        int step = 1;
        int N = arr.length;
        int L = 0;//左组第一个位置
        //一次性申请辅助空间
        int [] help = new int[arr.length];

        while (step < N){
            L = 0;//每次第一个位置应该都是0
            //L位置不能超过数组长度
            while (L < N){
                //分组后左组最后一个数位置
                int M = L + step -1;
                //左组最后一个位置超过数组长度
                if(M >= N){
                    break;
                }
                //如果分组最后一组只满足左组，右组没有值时，该小组不用排序
                // N -L 最后一组的左组，步长 >=，说明只有左组，没有右组，不进行排序
                if(step >= N-L){
                    break;
                }
                //计算右组最后一个位置，右组开始位置位 M+1
                int R = Math.min(M+step,N-1);

                //合并左右组
                merge(arr,L,M,R,help);

                //合并后进行下一小组
                L = R + 1;

            }
            //防止溢出，如果N很接近整数最大值，当step来到接近N时，乘2就溢出了
            if(step > N>>2){
                break;
            }
            //步长翻倍
            //左移一位等价于 *2
            step <<=1;
        }
    }


    //合并排序arr[L,mid]和arr[mid+1,R]
    //申请一个辅助数组，长度位L和R的之间长度，用于保存排序后的结果
    //p1为左侧开始位，p2为右侧开始位
    //对比排序后，将剩余数记录到help中
    public static void merge(int [] arr,int L,int mid,int R,int [] help){
        int i = 0;
        //对比开始位置
        int p1 = L,p2 = mid+1;
        //对比限制
        while (p1 <= mid && p2 <= R){
            //如果arr[p1] <= arr[p2]则将arr[p1]放入help中 ,然后p1++ ,i++
            //否则 将arr[p2]放入help中，然后 p2++,i++
            help[i++] = arr[p1]<=arr[p2]?arr[p1++]:arr[p2++];
        }
        //将剩余数放入help中
        while (p1<=mid){
           help[i++] = arr[p1++];
        }
        while (p2<=R){
           help[i++] = arr[p2++];
        }
        //将help中数放到arr中
        for(i=0;i<R-L+1;i++){
           arr[L+i] = help[i];
        }
    }