大数据(八)：Pandas的基础应用详解(五)

专栏介绍

结合自身经验和内部资料总结的Python教程，每天3-5章，最短1个月就能全方位的完成Python的学习并进行实战开发，学完了定能成为大佬！加油吧！卷起来！

全部文章请访问专栏：《Python全栈教程（0基础）》
再推荐一下最近热更的：《大厂测试高频面试题详解》该专栏对近年高频测试相关面试题做详细解答，结合自己多年工作经验，以及同行大佬指导总结出来的。旨在帮助测试、python方面的同学，顺利通过面试，拿到自己满意的offer！

文章目录

- 专栏介绍
- Pandas的基础应用详解(五)
- - DataFrame的应用
  - - 窗口计算
    - 相关性判定
  - Index的应用
  - - 范围索引（RangeIndex）
    - 分类索引（CategoricalIndex）
    - 多级索引（MultiIndex）
    - 日期时间索引（DatetimeIndex）

Pandas的基础应用详解(五)

DataFrame的应用

窗口计算

DataFrame对象的rolling方法允许我们将数据置于窗口中，然后就可以使用函数对窗口中的数据进行运算和处理。例如，我们获取了某只股票近期的数据，想制作5日均线和10日均线，那么就需要先设置窗口再进行运算。我们可以使用三方库pandas-datareader来获取指定的股票在某个时间段内的数据，具体的操作如下所示。

安装pandas-datareader三方库。

pip install pandas-datareader

通过pandas-datareader 提供的get_data_stooq从 Stooq 网站获取百度（股票代码：BIDU）近期股票数据。

import pandas_datareader as pdr

baidu_df = pdr.get_data_stooq('BIDU', start='2021-11-22', end='2021-12-7')
baidu_df.sort_index(inplace=True)
baidu_df

输出：

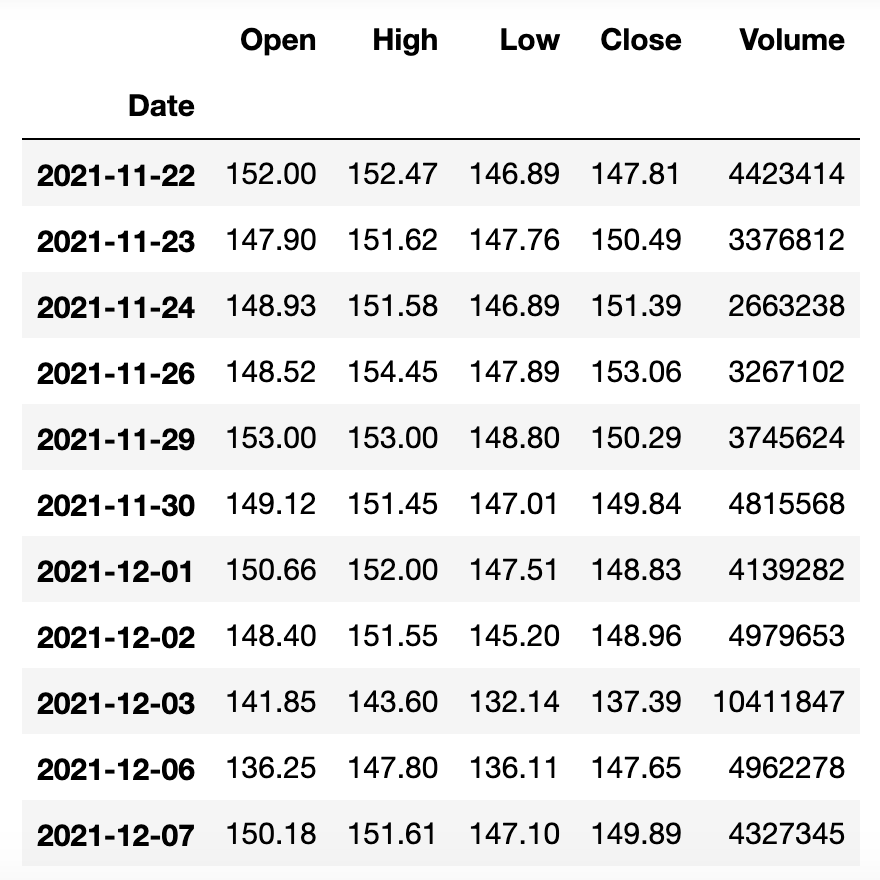
在这里插入图片描述

上面的DataFrame有Open、High、Low、Close、Volume五个列，分别代码股票的开盘价、最高价、最低价、收盘价和成交量，接下来我们对百度的股票数据进行窗口计算。

baidu_df.rolling(5).mean()

输出：

上面的Close 列的数据就是我们需要的5日均线，当然，我们也可以用下面的方法，直接在Close列对应的Series对象上计算5日均线。

baidu_df.Close.rolling(5).mean()

输出：

Date
2021-11-22        NaN
2021-11-23        NaN
2021-11-24        NaN
2021-11-26        NaN
2021-11-29    150.608
2021-11-30    151.014
2021-12-01    150.682
2021-12-02    150.196
2021-12-03    147.062
2021-12-06    146.534
2021-12-07    146.544
Name: Close, dtype: float64

相关性判定

在统计学中，我们通常使用协方差（covariance）来衡量两个随机变量的联合变化程度。如果变量 $X$ 的较大值主要与另一个变量 $Y$ 的较大值相对应，而两者较小值也相对应，那么两个变量倾向于表现出相似的行为，协方差为正。如果一个变量的较大值主要对应于另一个变量的较小值，则两个变量倾向于表现出相反的行为，协方差为负。简单的说，协方差的正负号显示着两个变量的相关性。方差是协方差的一种特殊情况，即变量与自身的协方差。

$\mu)(Y - \upsilon)) = E(X \cdot Y) - \mu\upsilon$

如果 $X$ 和 $Y$ 是统计独立的，那么二者的协方差为0，这是因为在 $X$ 和 $Y$ 独立的情况下：

$\cdot Y) = E(X) \cdot E(Y) = \mu\upsilon$

协方差的数值大小取决于变量的大小，通常是不容易解释的，但是正态形式的协方差大小可以显示两变量线性关系的强弱。在统计学中，皮尔逊积矩相关系数就是正态形式的协方差，它用于度量两个变量 $X$ 和 $Y$ 之间的相关程度（线性相关），其值介于-1到1之间。

$\rho{X,Y} = \frac {cov(X, Y)} {\sigma_{X}\sigma_{Y}}$

估算样本的协方差和标准差，可以得到样本皮尔逊系数，通常用希腊字母 $\rho$ 表示。

$\rho = \frac {\sum_{i=1}^{n}(X_i - \bar{X})(Y_i - \bar{Y})} {\sqrt{\sum_{i=1}^{n}(X_i - \bar{X})^2} \sqrt{\sum_{i=1}^{n}(Y_i - \bar{Y})^2}}$

我们用 $\rho$ 值判断指标的相关性时遵循以下两个步骤。

判断指标间是正相关、负相关，还是不相关。
- 当 $ \rho \gt 0 $，认为变量之间是正相关，也就是两者的趋势一致。
- 当 $ \rho \lt 0 $，认为变量之间是负相关，也就是两者的趋势相反。
- 当 $ \rho = 0 $，认为变量之间是不相关的，但并不代表两个指标是统计独立的。
判断指标间的相关程度。
- 当 $ \rho $ 的绝对值在 $ [0.6,1] $ 之间，认为变量之间是强相关的。
- 当 $ \rho $ 的绝对值在 $ [0.1,0.6) $ 之间，认为变量之间是弱相关的。
- 当 $ \rho $ 的绝对值在 $ [0,0.1) $ 之间，认为变量之间没有相关性。

皮尔逊相关系数适用于：

两个变量之间是线性关系，都是连续数据。
两个变量的总体是正态分布，或接近正态的单峰分布。
两个变量的观测值是成对的，每对观测值之间相互独立。

DataFrame对象的cov方法和corr方法分别用于计算协方差和相关系数，corr方法的第一个参数method的默认值是pearson，表示计算皮尔逊相关系数；除此之外，还可以指定kendall或spearman来获得肯德尔系数或斯皮尔曼等级相关系数。

接下来，我们从名为boston_house_price.csv的文件中获取著名的波士顿房价数据集来创建一个DataFrame，我们通过corr方法计算可能影响房价的13个因素中，哪些跟房价是正相关或负相关的，代码如下所示。

boston_df = pd.read_csv('data/csv/boston_house_price.csv')
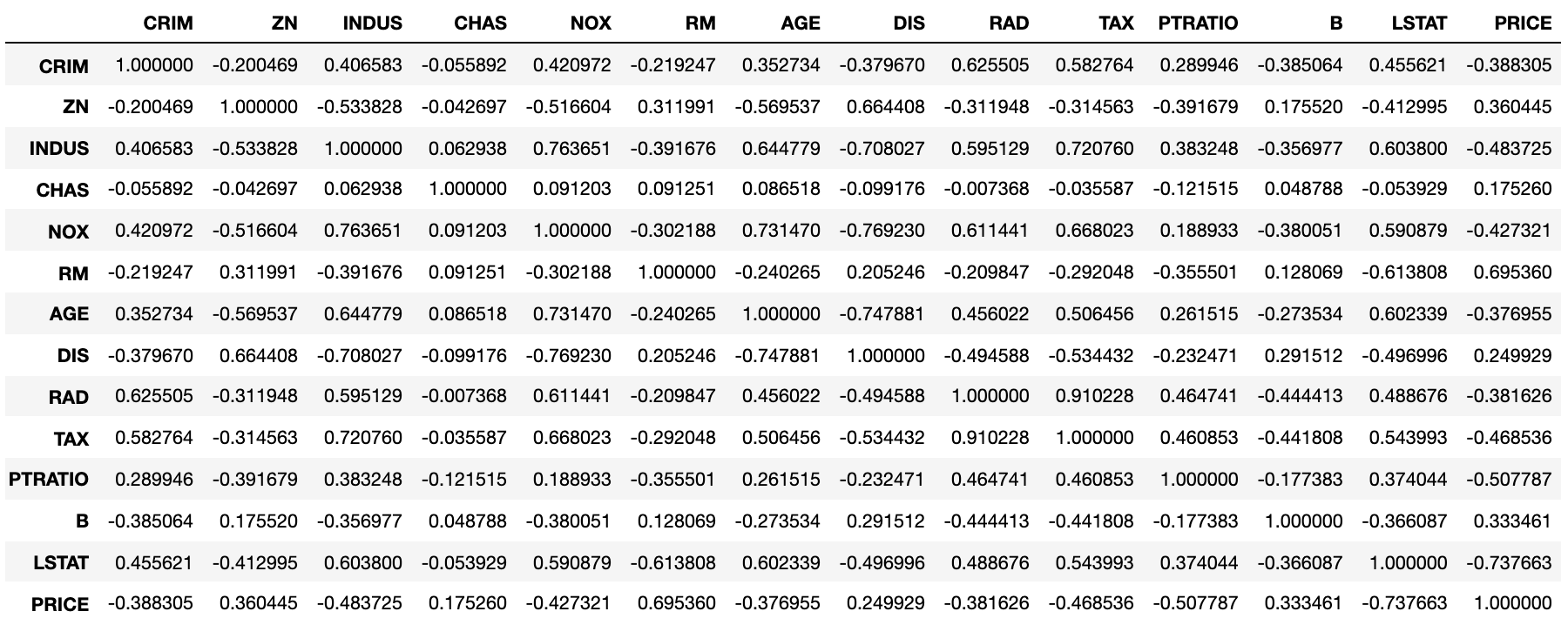
boston_df.corr()

说明：如果需要上面例子中的 CSV 文件，可以通过下面的百度云盘地址进行获取，数据在《从零开始学数据分析》目录中。链接：https://pan.baidu.com/s/1rQujl5RQn9R7PadB2Z5g_g，提取码：e7b4。

输出：

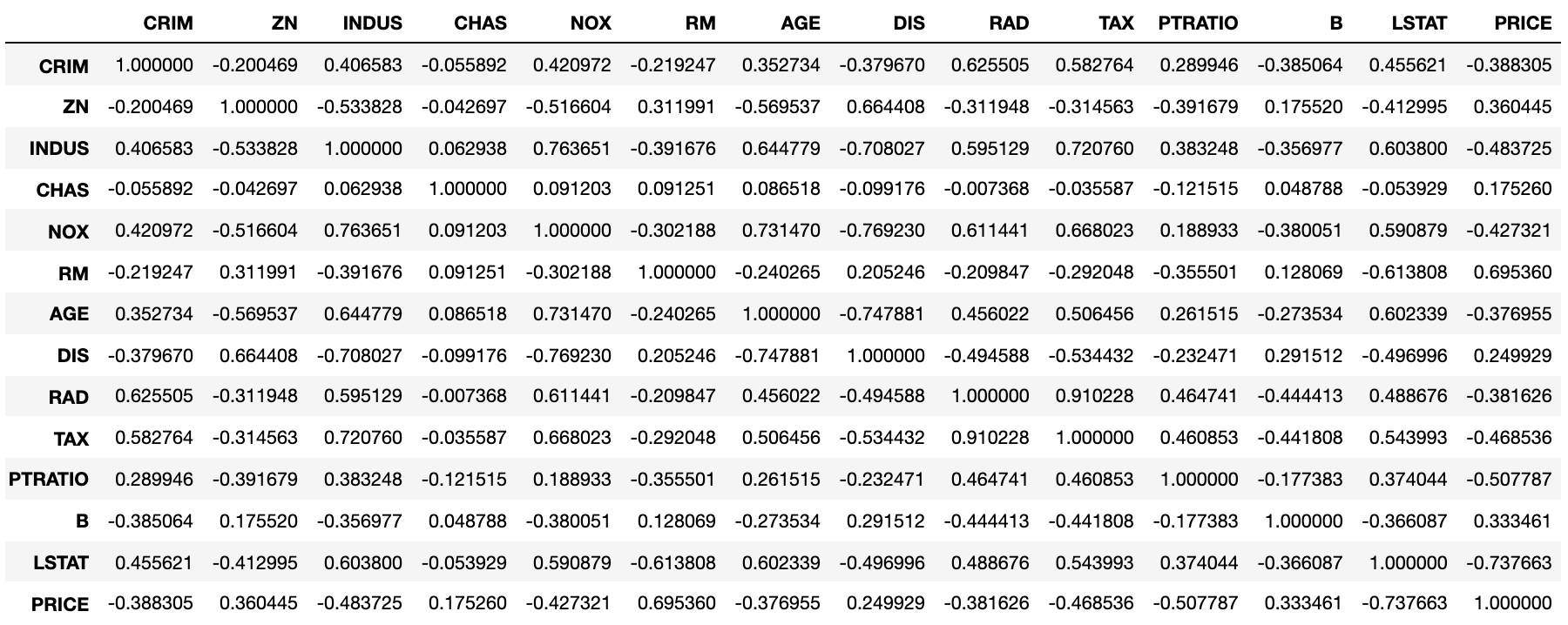
在这里插入图片描述

斯皮尔曼相关系数对数据条件的要求没有皮尔逊相关系数严格，只要两个变量的观测值是成对的等级评定资料，或者是由连续变量观测资料转化得到的等级资料，不论两个变量的总体分布形态、样本容量的大小如何，都可以用斯皮尔曼等级相关系数来进行研究。我们通过下面的方式来计算斯皮尔曼相关系数。

boston_df.corr('spearman')

输出：

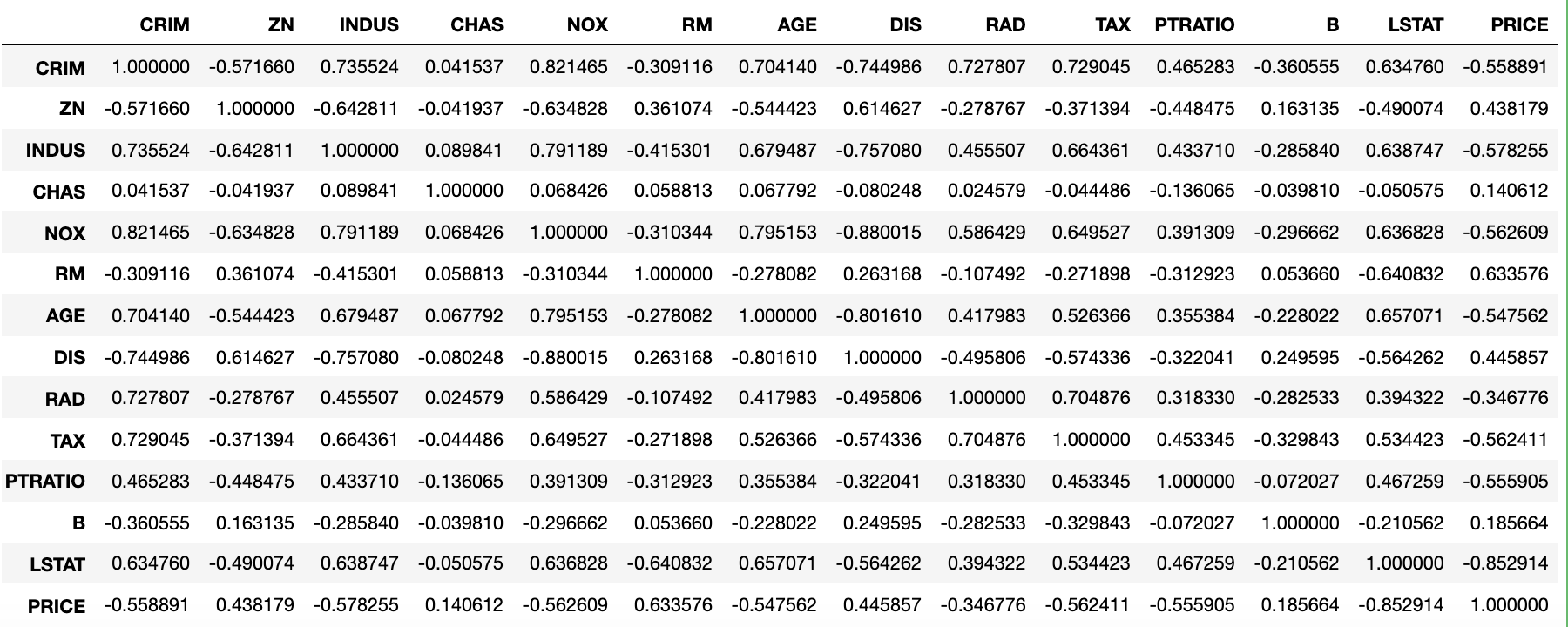
在 Notebook 或 JupyterLab 中，我们可以为PRICE列添加渐变色，用颜色直观的展示出跟房价负相关、正相关、不相关的列，DataFrame对象style属性的background_gradient方法可以完成这个操作，代码如下所示。

boston_df.corr('spearman').style.background_gradient('RdYlBu', subset=['PRICE'])

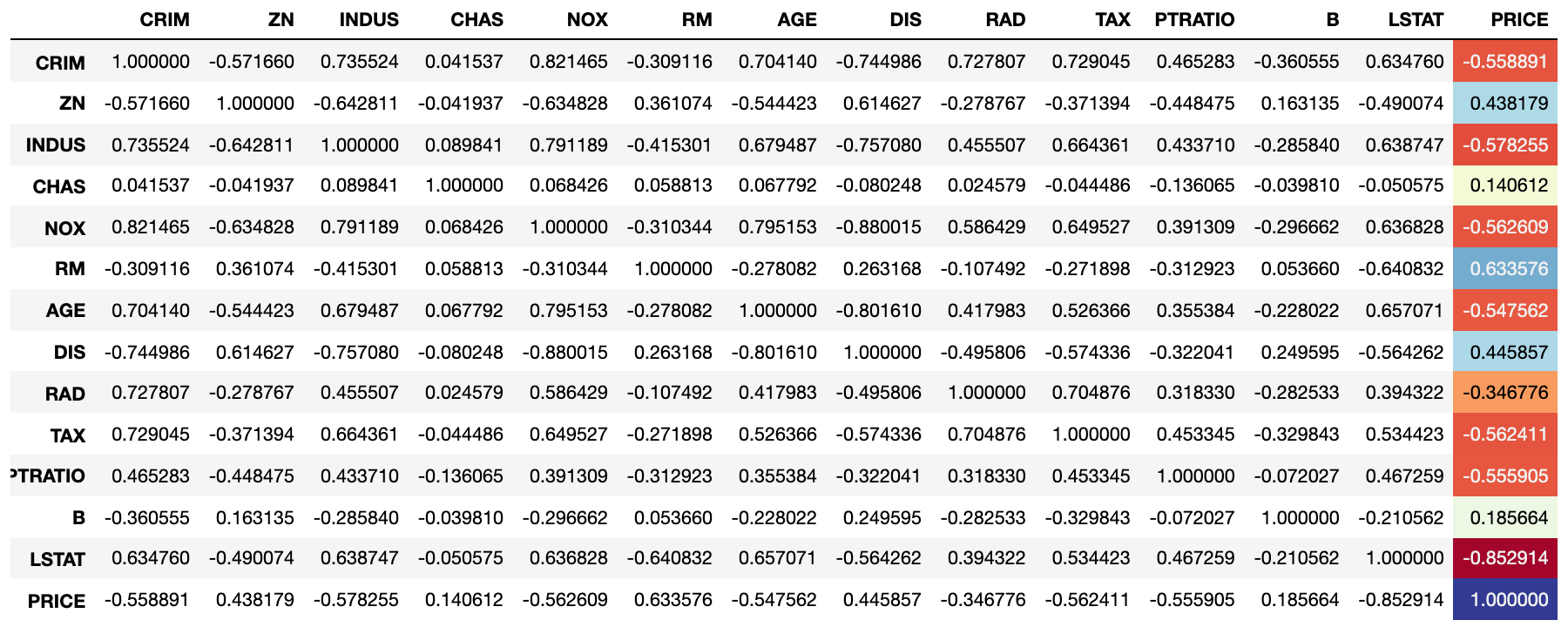
上面代码中的RdYlBu代表的颜色如下所示，相关系数的数据值越接近1，颜色越接近红色；数据值越接近1，颜色越接近蓝色；数据值在0附件则是黄色。

plt.get_cmap('RdYlBu')

在这里插入图片描述

Index的应用

我们再来看看Index类型，它为Series和DataFrame对象提供了索引服务，常用的Index有以下几种。

范围索引（RangeIndex）

代码：

sales_data = np.random.randint(400, 1000, 12)
month_index = pd.RangeIndex(1, 13, name='月份')
ser = pd.Series(data=sales_data, index=month_index)
ser

输出：

月份
1     703
2     705
3     557
4     943
5     961
6     615
7     788
8     985
9     921
10    951
11    874
12    609
dtype: int64

分类索引（CategoricalIndex）

代码：

cate_index = pd.CategoricalIndex(
    ['苹果', '香蕉', '苹果', '苹果', '桃子', '香蕉'],
    ordered=True,
    categories=['苹果', '香蕉', '桃子']
)
ser = pd.Series(data=amount, index=cate_index)
ser

输出：

苹果    6
香蕉    6
苹果    7
苹果    6
桃子    8
香蕉    6
dtype: int64

代码：

ser.groupby(level=0).sum()

输出：

苹果    19
香蕉    12
桃子     8
dtype: int64

多级索引（MultiIndex）

代码：

ids = np.arange(1001, 1006)
sms = ['期中', '期末']
index = pd.MultiIndex.from_product((ids, sms), names=['学号', '学期'])
courses = ['语文', '数学', '英语']
scores = np.random.randint(60, 101, (10, 3))
df = pd.DataFrame(data=scores, columns=courses, index=index)
df

说明：上面的代码使用了MultiIndex的类方法from_product，该方法通过ids和sms两组数据的笛卡尔积构造了多级索引。

输出：

             语文 数学 英语
学号	学期			
1001  期中	93	77	60
      期末	93	98	84
1002  期中	64	78	71
      期末	70	71	97
1003  期中	72	88	97
      期末	99	100	63
1004  期中	80	71	61
      期末	91	62	72
1005  期中	82	95	67
      期末	84	78	86

代码：

# 计算每个学生的成绩，期中占25%，期末占75%
df.groupby(level=0).agg(lambda x: x.values[0] * 0.25 + x.values[1] * 0.75)

输出：

        语文    数学    英语
学号			
1001	93.00	92.75	78.00
1002	68.50	72.75	90.50
1003	92.25	97.00	71.50
1004	88.25	64.25	69.25
1005	83.50	82.25	81.25

日期时间索引（DatetimeIndex）

通过date_range()函数，我们可以创建日期时间索引，代码如下所示。

代码：

pd.date_range('2021-1-1', '2021-6-1', periods=10)

输出：

DatetimeIndex(['2021-01-01 00:00:00', '2021-01-17 18:40:00',
               '2021-02-03 13:20:00', '2021-02-20 08:00:00',
               '2021-03-09 02:40:00', '2021-03-25 21:20:00',
               '2021-04-11 16:00:00', '2021-04-28 10:40:00',
               '2021-05-15 05:20:00', '2021-06-01 00:00:00'],
              dtype='datetime64[ns]', freq=None)

代码：

pd.date_range('2021-1-1', '2021-6-1', freq='W')

输出：

DatetimeIndex(['2021-01-03', '2021-01-10', '2021-01-17', '2021-01-24',
               '2021-01-31', '2021-02-07', '2021-02-14', '2021-02-21',
               '2021-02-28', '2021-03-07', '2021-03-14', '2021-03-21',
               '2021-03-28', '2021-04-04', '2021-04-11', '2021-04-18',
               '2021-04-25', '2021-05-02', '2021-05-09', '2021-05-16',
               '2021-05-23', '2021-05-30'],
              dtype='datetime64[ns]', freq='W-SUN')

通过DateOffset类型，我们可以设置时间差并和DatetimeIndex进行运算，具体的操作如下所示。

代码：

index = pd.date_range('2021-1-1', '2021-6-1', freq='W')
index - pd.DateOffset(days=2)

输出：

DatetimeIndex(['2021-01-01', '2021-01-08', '2021-01-15', '2021-01-22',
               '2021-01-29', '2021-02-05', '2021-02-12', '2021-02-19',
               '2021-02-26', '2021-03-05', '2021-03-12', '2021-03-19',
               '2021-03-26', '2021-04-02', '2021-04-09', '2021-04-16',
               '2021-04-23', '2021-04-30', '2021-05-07', '2021-05-14',
               '2021-05-21', '2021-05-28'],
              dtype='datetime64[ns]', freq=None)

代码：

index + pd.DateOffset(days=2)

输出：

DatetimeIndex(['2021-01-05', '2021-01-12', '2021-01-19', '2021-01-26',
               '2021-02-02', '2021-02-09', '2021-02-16', '2021-02-23',
               '2021-03-02', '2021-03-09', '2021-03-16', '2021-03-23',
               '2021-03-30', '2021-04-06', '2021-04-13', '2021-04-20',
               '2021-04-27', '2021-05-04', '2021-05-11', '2021-05-18',
               '2021-05-25', '2021-06-01'],
              dtype='datetime64[ns]', freq=None)

可以使用DatatimeIndex类型的相关方法来处理数据，具体包括：
- shift()方法：通过时间前移或后移数据，我们仍然以上面百度股票数据为例，代码如下所示。
  
  代码：
```
baidu_df.shift(3, fill_value=0)
```
  输出：
  
  代码：
```
baidu_df.shift(-1, fill_value=0)
```
  输出：
- asfreq()方法：指定一个时间频率抽取对应的数据，代码如下所示。
  
  代码：
```
baidu_df.asfreq('5D')
```
  输出：

在这里插入图片描述

代码：

       baidu_df.asfreq('5D', method='ffill')

- `resample()`方法：基于时间对数据进行重采样，相当于根据时间周期对数据进行了分组操作，代码如下所示。

    代码：

    ```python
    baidu_df.resample('1M').mean()
    ```

> **说明**：上面的代码中，`W`表示一周，`5D`表示`5`天，`1M`表示`1`个月。

时区转换
- 获取时区信息。
```
import pytz

pytz.common_timezones
```
- tz_localize()方法：将日期时间本地化。
  
  代码：
```
baidu_df = baidu_df.tz_localize('Asia/Chongqing')
baidu_df
```
  输出：
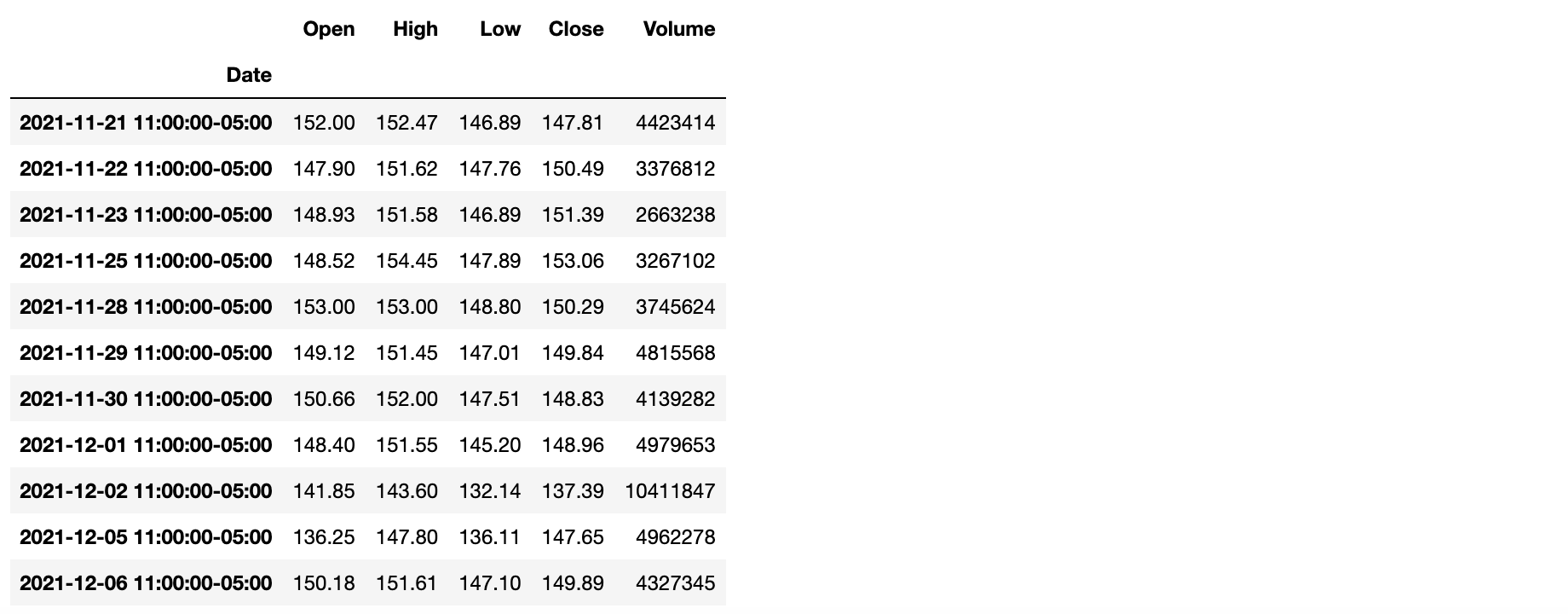
- tz_convert()方法：转换时区。
  
  代码：
```
baidu_df.tz_convert('America/New_York')
```
  输出：