题目 

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

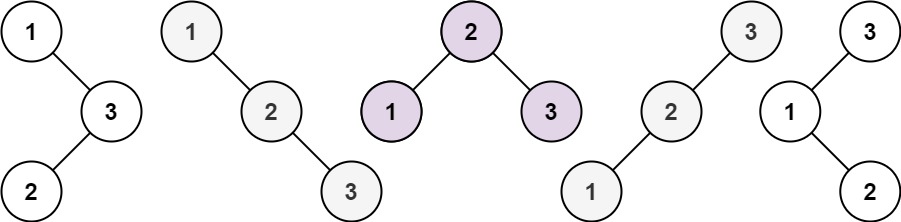
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 19

代码 

定义dp[i]为由i个节点组成的二叉排序树有dp[i]种。

我们可以从节点数i为2开始遍历，每次遍历分别用j表示根节点左子树有j个节点，那对应右子树就有i-j-1个节点，那么左右子树分别能够组成的二叉排序树就是dp[j]和dp[i-j-1]种 ，j的取值范围是从0到i-1。题目要求的就是dp[j]*dp[i-j-1]。

这里当左右子树有为空的时候，我们应该把他当成1，不然dp[j]*dp[i-j-1]就是0了，但这种情况也是合理的，因此处理一下得到：dp[i]+=max(1,dp[j])*max(1,dp[i-j-1])。

class Solution:
    def numTrees(self, n: int) -> int:
        dp = [0 for _ in range(n+1)]
        dp[1]=1

        for i in range(2,n+1):
            for j in range(i):
                dp[i]+=max(1,dp[j])*max(1,dp[i-j-1])
        return dp[n]