题目
力扣题目链接(opens new window)
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
- 序列中第一个单词是 beginWord 。
- 序列中最后一个单词是 endWord 。
- 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典 wordList 中的单词。
- 给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
- 输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
- 输出:5
- 解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2:
- 输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
- 输出:0
- 解释:endWord "cog" 不在字典中,所以无法进行转换。
思路
以示例1为例,从这个图中可以看出 hit 到 cog的路线,不止一条,有三条,一条是最短的长度为5,两条长度为6。
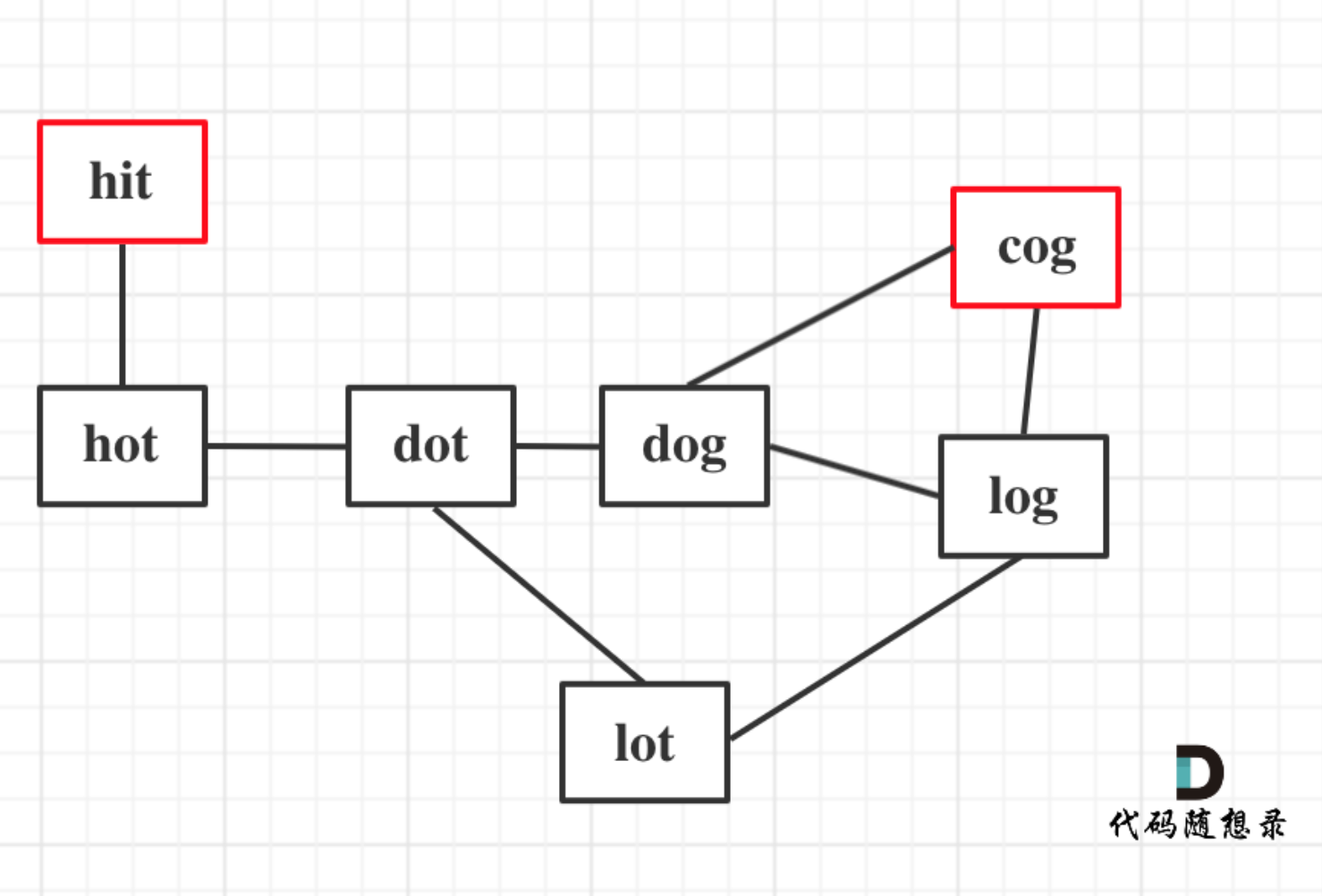
本题只需要求出最短路径的长度就可以了,不用找出路径。
所以这道题要解决两个问题:
- 图中的线是如何连在一起的
- 起点和终点的最短路径长度
首先题目中并没有给出点与点之间的连线,而是要我们自己去连,条件是字符只能差一个,所以判断点与点之间的关系,要自己判断是不是差一个字符,如果差一个字符,那就是有链接。
然后就是求起点和终点的最短路径长度,这里无向图求最短路,广搜最为合适,广搜只要搜到了终点,那么一定是最短的路径。因为广搜就是以起点中心向四周扩散的搜索。
本题如果用深搜,会比较麻烦,要在到达终点的不同路径中选则一条最短路。 而广搜只要达到终点,一定是最短路。
另外需要有一个注意点:
- 本题是一个无向图,需要用标记位,标记着节点是否走过,否则就会死循环!
- 本题给出集合是数组型的,可以转成set结构,查找更快一些
C++代码如下(详细注释)
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
// 将vector转成unordered_set,提高查询速度
unordered_set<string> wordSet(wordList.begin(), wordList.end());
// 如果endWord没有在wordSet出现,直接返回0
if (wordSet.find(endWord) == wordSet.end()) return 0;
// 记录word是否访问过
unordered_map<string, int> visitMap; // <word, 查询到这个word路径长度>
// 初始化队列
queue<string> que;
que.push(beginWord);
// 初始化visitMap
visitMap.insert(pair<string, int>(beginWord, 1));
while(!que.empty()) {
string word = que.front();
que.pop();
int path = visitMap[word]; // 这个word的路径长度
for (int i = 0; i < word.size(); i++) {
string newWord = word; // 用一个新单词替换word,因为每次置换一个字母
for (int j = 0 ; j < 26; j++) {
newWord[i] = j + 'a';
if (newWord == endWord) return path + 1; // 找到了end,返回path+1
// wordSet出现了newWord,并且newWord没有被访问过
if (wordSet.find(newWord) != wordSet.end()
&& visitMap.find(newWord) == visitMap.end()) {
// 添加访问信息
visitMap.insert(pair<string, int>(newWord, path + 1));
que.push(newWord);
}
}
}
}
return 0;
}
};
本题也可以用双向BFS,就是从头尾两端进行搜索。
知识点
unordered_set和unordered_map
unordered_set和unordered_map是C++ STL中的容器,用于存储不重复的元素。unordered_set用于存储唯一的元素集合,而unordered_map用于存储键值对的集合。
unordered_set的用法:
- 引入头文件:
#include <unordered_set>- 创建unordered_set对象:
unordered_set<int> mySet;- 添加元素:
mySet.insert(10);- 删除元素:
mySet.erase(10);- 判断元素是否存在:
mySet.count(10);- 遍历元素:使用迭代器进行遍历,例如:
for(auto it = mySet.begin(); it != mySet.end(); ++it) { cout << *it << " "; }unordered_map的用法:
- 引入头文件:
#include <unordered_map>- 创建unordered_map对象:
unordered_map<string, int> myMap;- 添加键值对:
myMap["apple"] = 1;- 删除键值对:
myMap.erase("apple");- 判断键是否存在:
myMap.count("apple");- 遍历键值对:使用迭代器进行遍历,例如:
for(auto it = myMap.begin(); it != myMap.end(); ++it) { cout << it->first << ": " << it->second << endl; }需要注意的是,unordered_set和unordered_map是基于哈希表实现的,因此元素的顺序是不确定的,不同的编译器和不同的运行环境可能会有不同的顺序。如果需要有序的集合或映射,可以使用set和map容器。
将vector转成unordered_set,提高查询速度
要将vector转换为unordered_set,可以使用unordered_set的构造函数,将vector的begin和end迭代器作为参数传递给构造函数。这样可以将vector中的元素一次性地插入到unordered_set中。
#include <unordered_set> #include <vector> int main() { std::vector<int> vec = {1, 2, 3, 4, 5}; std::unordered_set<int> set(vec.begin(), vec.end()); // 使用unordered_set进行查询 if(set.find(3) != set.end()) { // 找到了元素3 } return 0; }将vector转换为unordered_set可以提高查询速度的原因有两点:
- 哈希表的查询速度快:unordered_set是基于哈希表实现的,通过哈希函数将元素映射到不同的桶中,使得查询的平均时间复杂度为O(1)。相比于vector的线性查找,unordered_set的查询速度更快。
- 元素不重复:unordered_set中的元素是唯一的,不会出现重复的元素。当需要判断一个元素是否存在时,只需要通过哈希函数计算出元素的哈希值,然后在对应的桶中查找即可,不需要遍历整个集合。这样可以大大提高查询的效率。
需要注意的是,unordered_set的插入和查询操作的平均时间复杂度是O(1),但最坏情况下的时间复杂度是O(n),其中n是unordered_set中的元素个数。因此,在实际使用中,还需要根据具体的情况选择合适的容器。