动态规划——最长公共子串

题目链接

https://www.nowcoder.com/practice/98dc82c094e043ccb7e0570e5342dd1b?tpId=37&tqId=21298&rp=1&ru=/exam/oj/ta&qru=/exam/oj/ta&sourceUrl=%2Fexam%2Foj%2Fta%3FjudgeStatus%3D3%26page%3D2%26pageSize%3D50%26search%3D%26tpId%3D37%26type%3D37&difficulty=undefined&judgeStatus=3&tags=&title=
思路

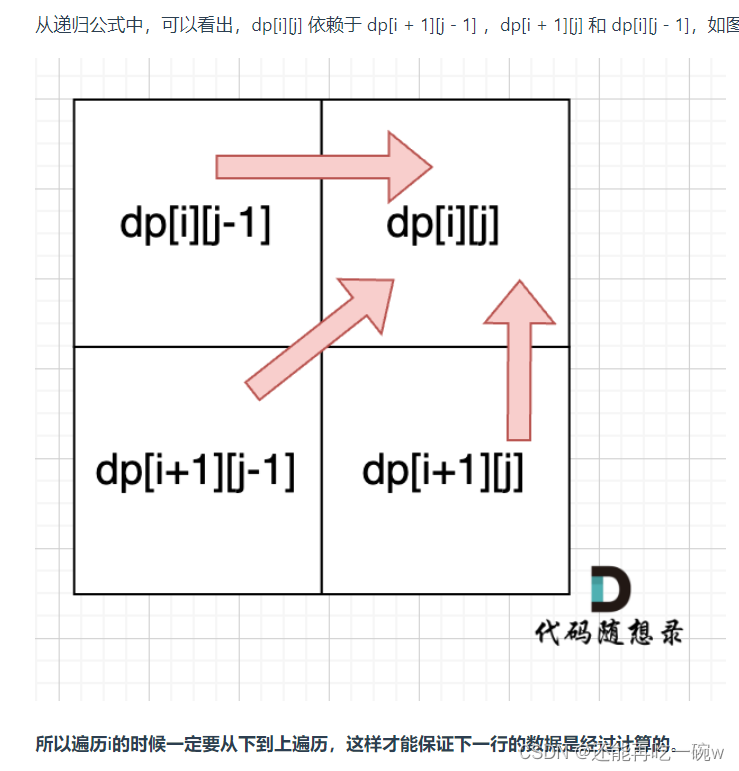
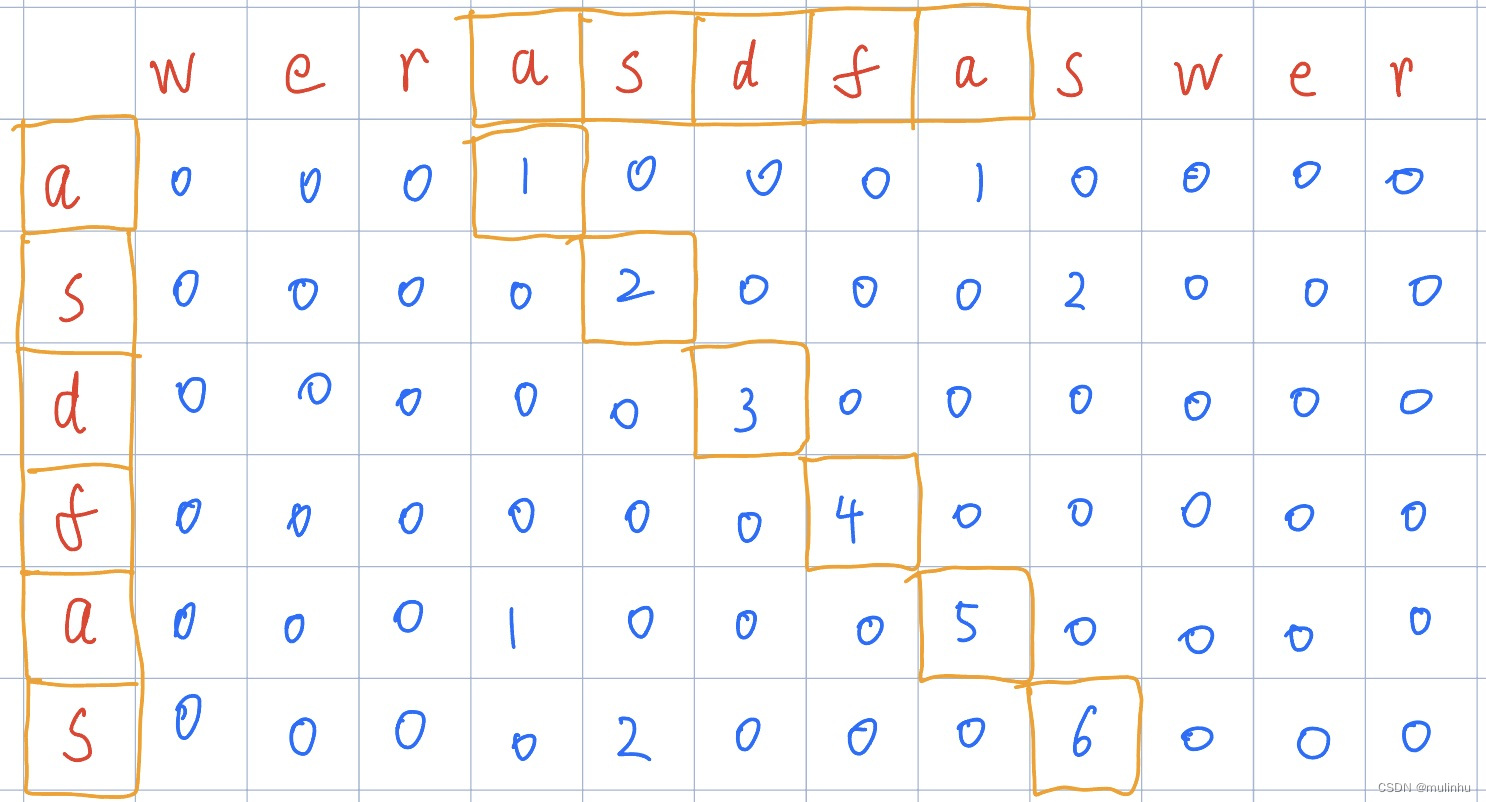
定义dp[i][j]为s1和s2分别以s1[i]和s2[j]为结尾的两个公共子串的长度。当dp[i][j]=0时说明s1[i]!=s2[j]。
转移方程为dp[i][j] = dp[i-1][j-1] if(s1[i] == s2[j])

#include <iostream>
#include <vector>
#include <string>

using namespace std;

int main() {
    string line1,line2;
    cin>>line1>>line2;
    int m = line1.size();
    int n = line2.size();
     int mx = 0;
    vector<vector<int>> dp(m,vector<int>(n,0));
    for(int i=0;i<m;i++){
        if(line1[i]==line2[0])dp[i][0] = 1;
        mx  = max(mx,dp[i][0]);
    }
    for(int j=0;j<n;j++){
        if(line1[0] == line2[j])dp[0][j] = 1;
        mx  = max(mx,dp[0][j]);
    }
   
    for(int i=1;i<m;i++){
        for(int j=1;j<n;j++){
            if(line1[i]==line2[j])dp[i][j] = dp[i-1][j-1]+1;
            mx  = max(mx,dp[i][j]);
        }
    }
    cout<<mx<<endl;
}
// 64 位输出请用 printf("%lld")