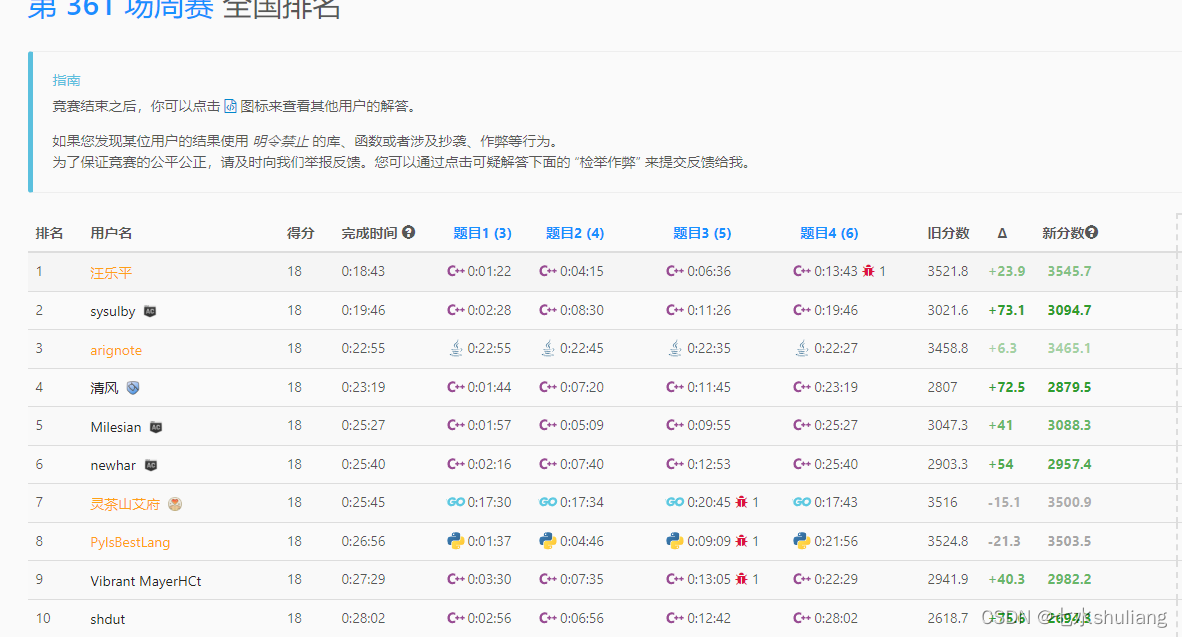
[LeetCode周赛复盘] 第 361 场周赛20230906
- 一、本周周赛总结
- 2843. 统计对称整数的数目
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 2844. 生成特殊数字的最少操作
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 2845. 统计趣味子数组的数目
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 2846. 边权重均等查询
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 参考链接
一、本周周赛总结
- 幸好上周练习了倍增,否则T4就垮了。
- T1 数位DP。
- T2 贪心。
- T3 同余+前缀和计数。
- T4 树上前缀和+lca。
2843. 统计对称整数的数目
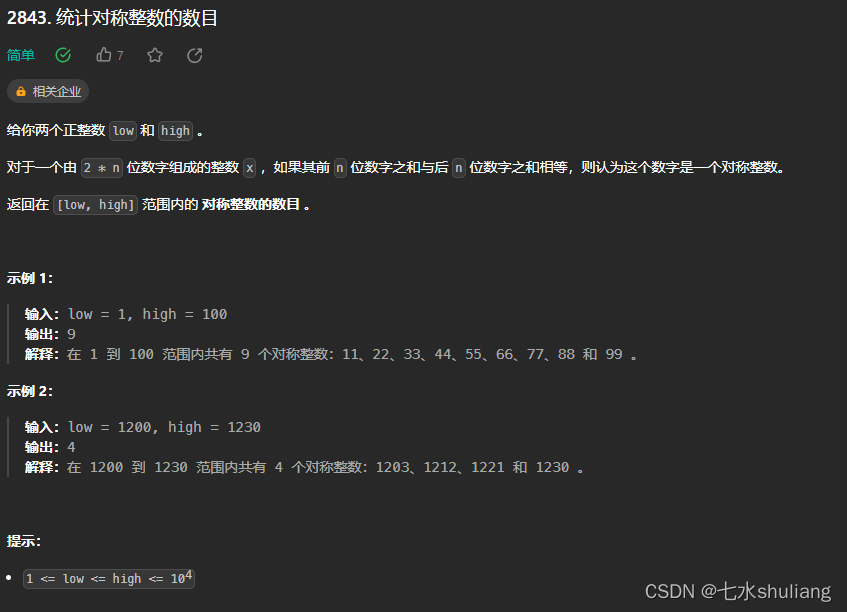
2843. 统计对称整数的数目
1. 题目描述
2. 思路分析
这个数据范围实际上可以枚举。
- 当困难题用数位DP做,可以达到log2high。
- 注意,两边的和可以合并成一个diff,如果不合并就是立方复杂度。
- 递归时,只需要多传递一个填数起始点,就可以计算出这个数的长度,以及填数时是算左边还是右边。
- 另外,这种high-low的以后一律写减法,尽量不考虑一个dfs同时搞上下界,思维量大很多。
3. 代码实现
class Solution:
def countSymmetricIntegers(self, low: int, high: int) -> int:
def f(s):
n = len(s)
@cache
def f(i,p,st,is_limit): # i,(suml-sumr),数字起点位置(代替is_num)
if p<0:return 0
if i == n:
return int(st!=-1 and p == 0)
ans = 0
if st==-1:
ans += f(i+1,p,-1,False)
if st != -1 or (n-i)%2 == 0: # 只有偶数长度有意义
up = int(s[i]) if is_limit else 9
down = 1 if st==-1 else 0
if st == -1:
st = i
mid = st+(n-st)//2
d = 1 if i < mid else -1
for j in range(down,up+1):
ans += f(i+1,p+j*d,st,is_limit and up == j)
return ans
return f(0,0,-1,True)
return f(str(high)) - f(str(low-1))
2844. 生成特殊数字的最少操作
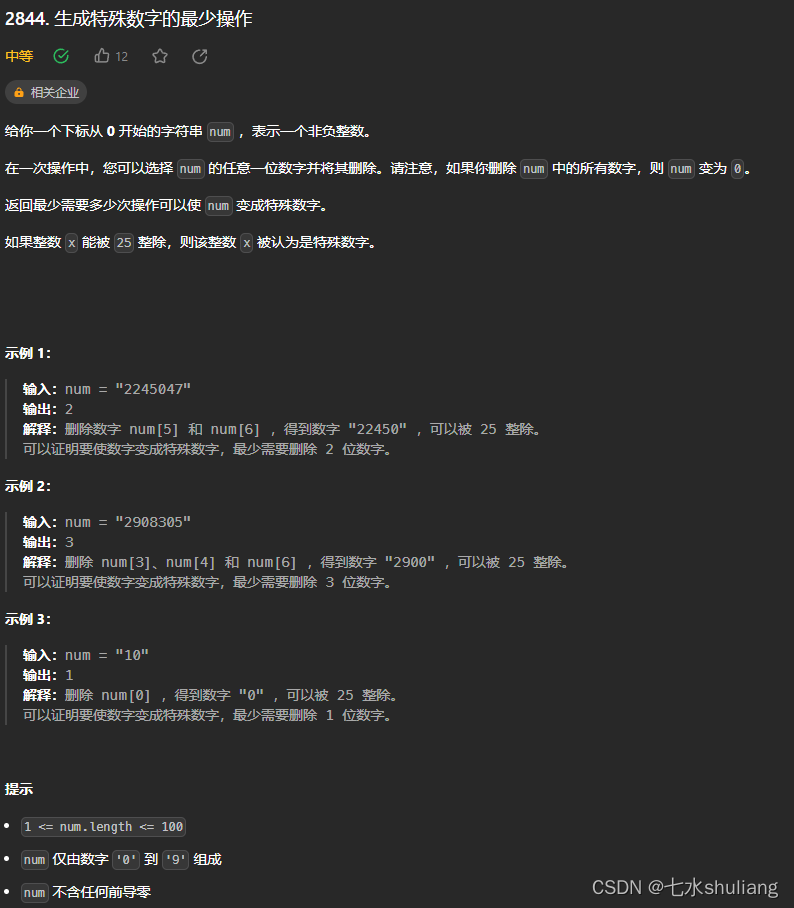
2844. 生成特殊数字的最少操作
1. 题目描述
2. 思路分析
- 能被25整除的数字,末两位一定是 00,25,50,75。
- 那么从末尾依次找这几个字符即可,能找到第二个字符,就是途经的长度-1。
- 另外,如果都没找到,至少可以把除了0的全删除,变成0也视为合法,即删除n-count(0)个。
3. 代码实现
class Solution:
def minimumOperations(self, num: str) -> int:
n = len(num)
num = num[::-1]
five = zero = -1
for i,v in enumerate(num):
if v == '5':
if zero != -1:
return i - 1
five = i
elif v == '0':
if zero != -1:
return i-1
zero = i
elif v == '2' or v == '7':
if five != -1:
return i-1
return n - num.count('0')
2845. 统计趣味子数组的数目
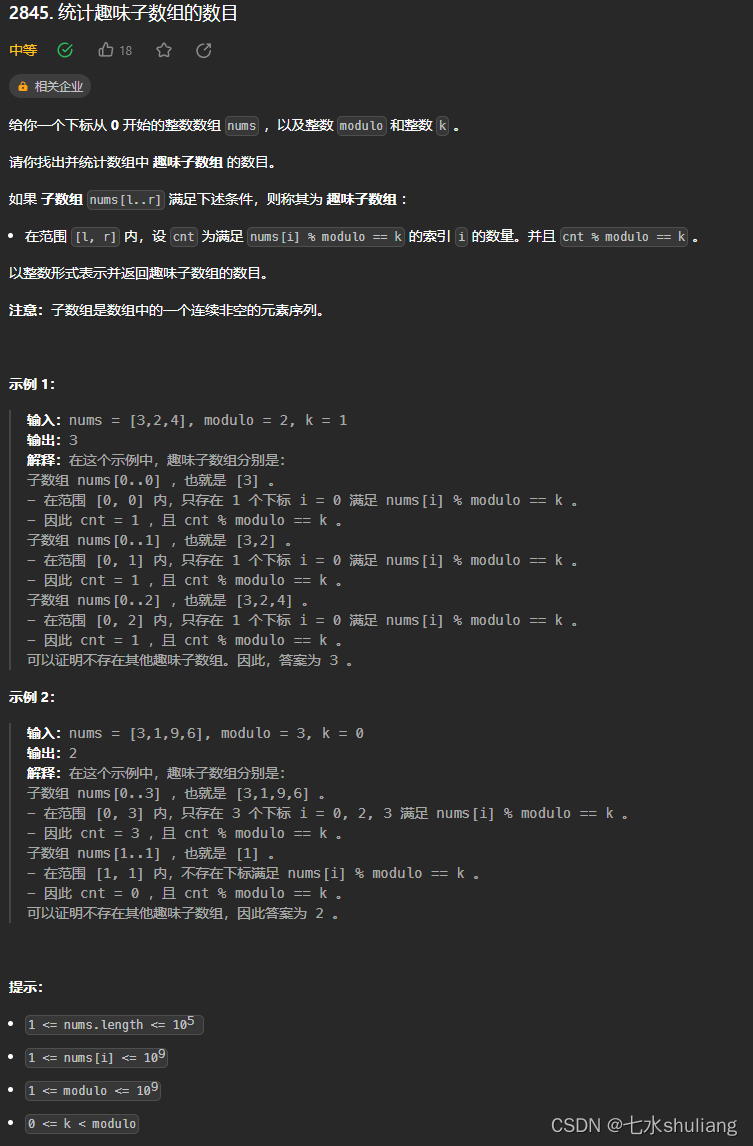
2845. 统计趣味子数组的数目
1. 题目描述
2. 思路分析
- 典题,同余计数。
- 第一个条件可以看成nums全是01,那么题目变成问有多少子段,和 ≡ k(% mod)。
- 那么可以用前缀和+计数,假设当前右端点和为s,需求s-x = k,变化得x = s-k。
- 即它可以和所有(s-k)%mod的左端点组合,只需记录每个前缀和数量。
3. 代码实现
class Solution:
def countInterestingSubarrays(self, nums: List[int], modulo: int, k: int) -> int:
n = len(nums)
a = [int(v%modulo==k) for v in nums]
# cnt = [1]+[0]*n # re 下标范围应该是module不是n
cnt = Counter([0])
s = ans = 0
for v in a:
s += v
ans += cnt[(s-k)%modulo]
cnt[s%modulo] += 1
return ans
2846. 边权重均等查询
2846. 边权重均等查询
1. 题目描述
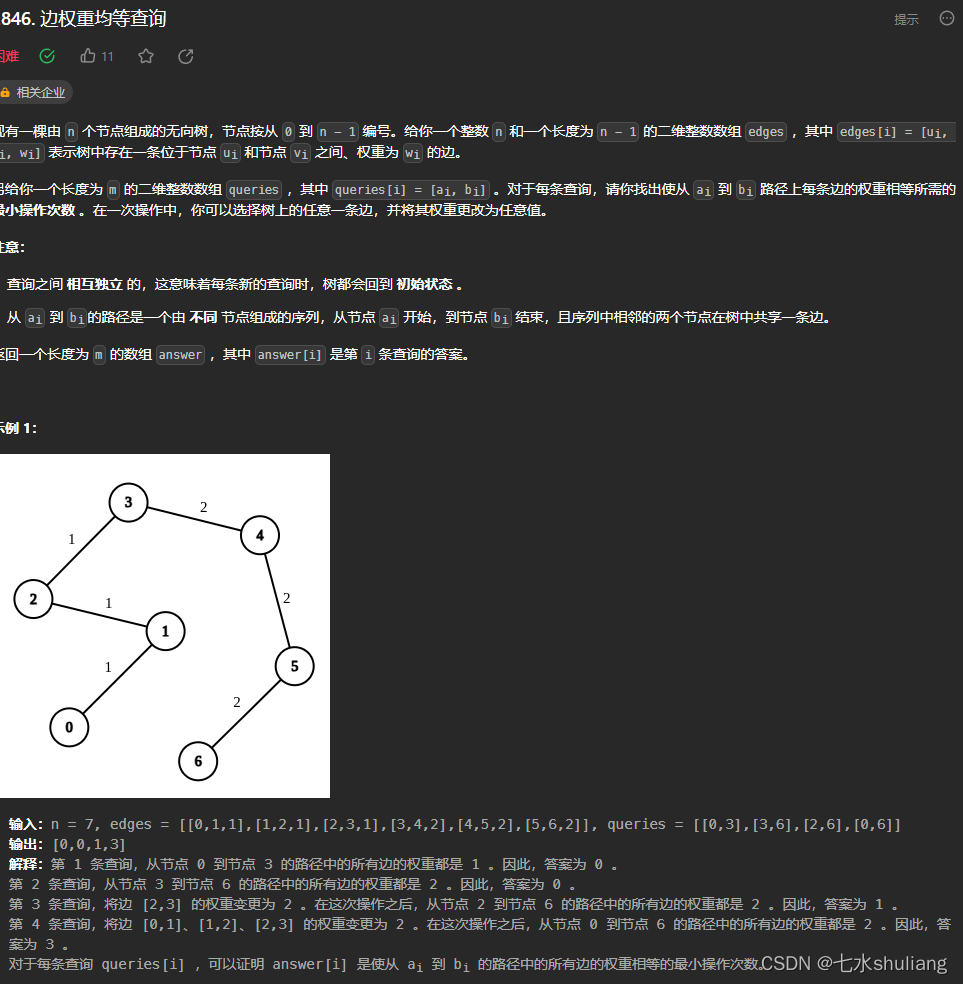
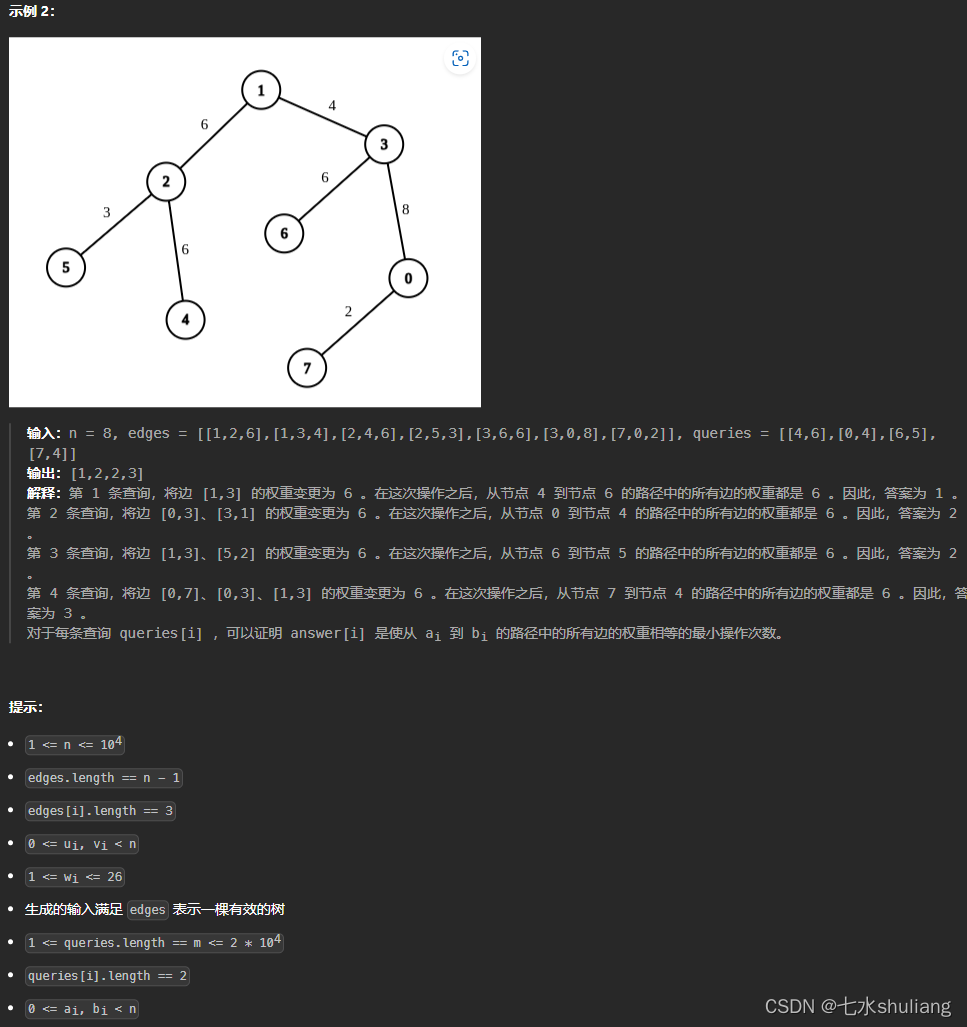
2. 思路分析
- 设一条长为a的路径上最多的权出现b次,那么修改次数就是a-b。则本题转化成:求任意路径的长度和边权最大频次。
- 看到边权值域只有26,考虑在值域上暴力计数。
- 如何求子段上的一条路径贡献呢,如果是一维数组我们通常考虑前缀和。这里是树,也是可以的。
- 有了快速计算子段的方法,还要考虑树的特殊计算方法。
- 两个点可能分别在两个子树里,可以画图思考一下。
- 计算时则可以先求出lca,画图发现:如果u是v的祖先,则可以套用普通的前缀和(祖先可以用lca==u来判断);否则,是两边加起来,再减去两次lca的前缀和;而第二种其实包含了第一种。
3. 代码实现
class Solution:
def minOperationsQueries(self, n: int, edges: List[List[int]], queries: List[List[int]]) -> List[int]:
g = [[] for _ in range(n)]
for u,v,w in edges:
g[v].append((u,w))
g[u].append((v,w))
m = n.bit_length()
pa = [[-1]*m for _ in range(n)]
pre=[[0]*27 for _ in range(n)]
s = [0]*27
depth = [0]*n
def dfs(u,fa,ww):
s[ww] += 1
pre[u] = s[:]
pa[u][0] = fa
for v,w in g[u]:
if v == fa:continue
depth[v] = depth[u] + 1
dfs(v,u,w)
s[ww] -= 1
dfs(0,-1,0)
for j in range(m-1):
for i in range(n):
p = pa[i][j]
pa[i][j+1] = pa[p][j]
def get_kth_ancestor(u,k):
for i in range(k.bit_length()):
if k>>i&1:
u = pa[u][i]
return u
def get_lca(u,v):
if depth[u] > depth[v]:
u,v = v,u
v = get_kth_ancestor(v,depth[v]-depth[u])
if u == v:
return u
for j in range(m-1,-1,-1):
pu,pv = pa[u][j],pa[v][j]
if pu != pv:
u,v = pu,pv
return pa[u][0]
ans = []
# for u,v in queries:
# p = [0]*27
# if depth[u] > depth[v]:
# u,v = v,u
# lca = get_lca(u,v)
# if lca == u:
# for i,(x,y) in enumerate(zip(pre[u],pre[v])):
# p[i] += y-x
# else:
# for i,(x,y,z) in enumerate(zip(pre[u],pre[v],pre[lca])):
# p[i] += y+x-2*z
# p[0] = 0
# ans.append(sum(p)-max(p))
for u,v in queries:
p = [0]*27
lca = get_lca(u,v)
for i,(x,y,z) in enumerate(zip(pre[u],pre[v],pre[lca])):
p[i] += y+x-2*z
ans.append(sum(p)-max(p))
return ans