一、说明
k-mean算法是一种聚类算法,它的主要思想是基于数据点之间的距离进行聚类。K-means聚类是一种无监督的机器学习算法。让我们再解释一下这句话。聚类分析的目标是将数据划分为同类聚类。每个聚类中的点彼此之间比其他聚类中的点更相似。
无监督机器学习是在没有任何标签的数据集上进行训练的。目标是发现数据中的模式或关系,而不是根据一组标记的示例进行预测。
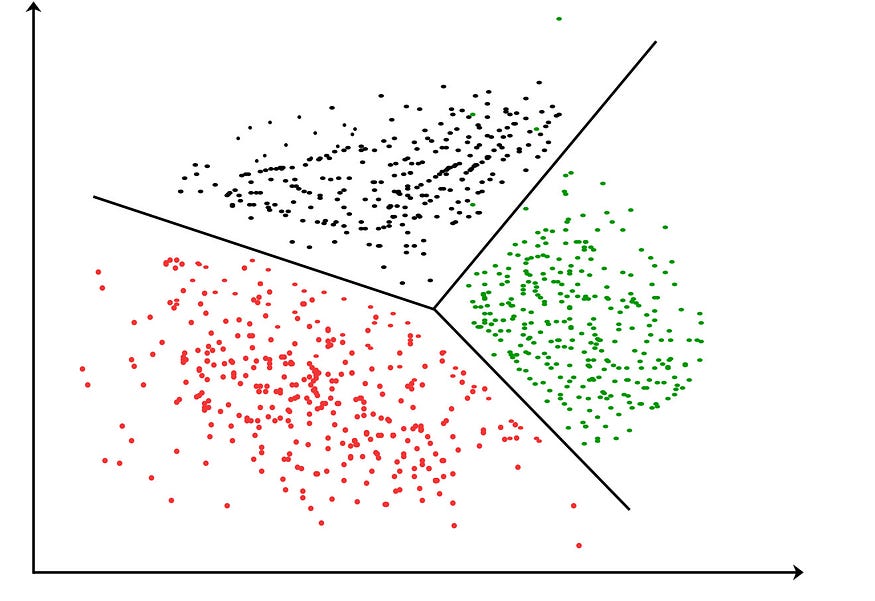
K 均值算法以迭代方式将数据点分配给最近的聚类中心,并根据分配点的均值更新聚类中心。目标是最小化数据点与其最近的聚类中心之间的平方距离之和。
K 是指定聚类数的超参数。
二、算法
输入:K 和点 x1,x2,...,xn
将质心放置在随机 c1,c2,...,ck 位置
重复直到收敛
-对于每个点 xi
- 计算距离并找到最近的质心 cj,argmin D (xi,cj),即欧几里得。
- 将点 XI 标记为集群 CJ
-对于每个簇 j = 1...K;
- 质心 CJ 的新位置是其所有点 XI 的平均值。
当集群的位置没有变化时结束它。
复杂度:O (#iterations * #clusters * #instances * #dimensions)
让我们可视化这些算法步骤,以便更好地理解。假设我们有如下所示的二维数据。我们还确定了 2 作为 K 个簇的数量。首先,让我们将 2 个质心放在随机位置。
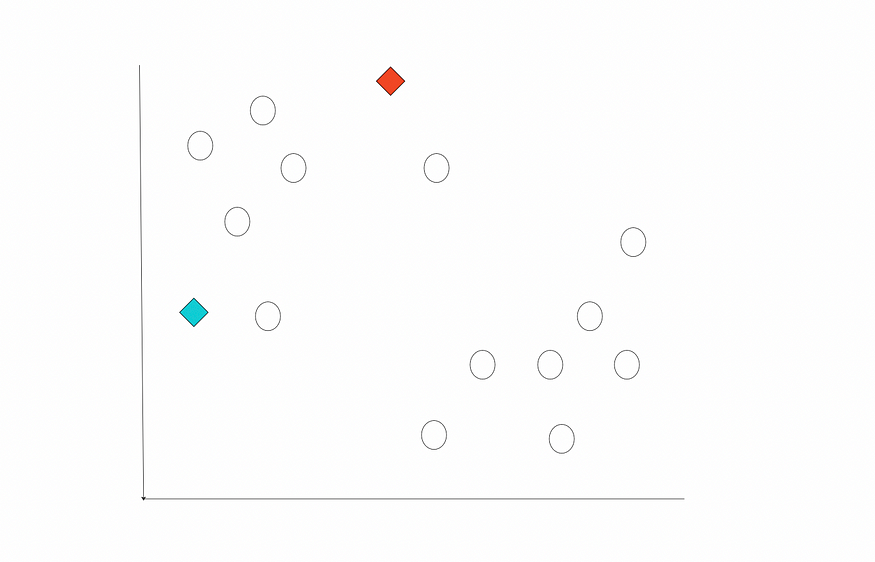
随机质心。图片由作者提供。
然后,我们计算每个点的欧几里得距离并分配标签。

分配标签。图片由作者提供。
计算每个聚类的新中心并将质心移动到新位置。
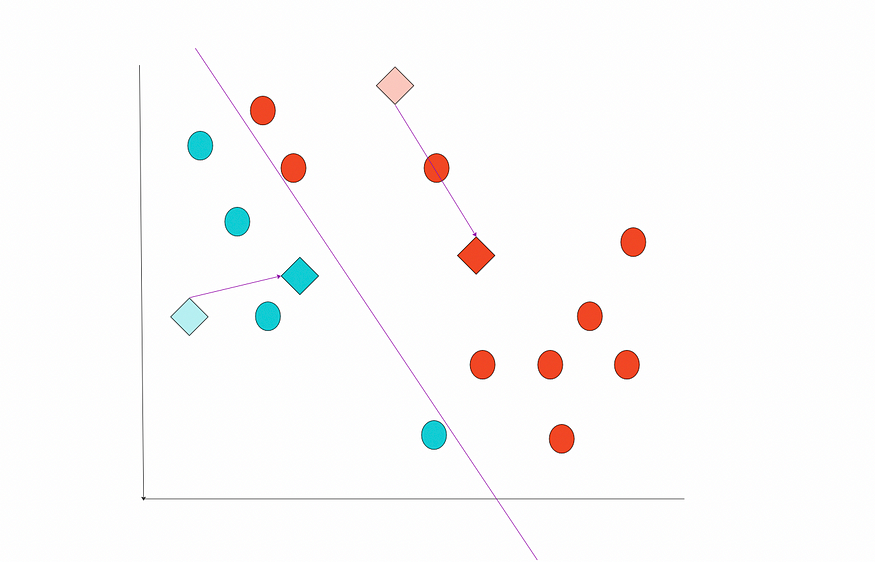
质心的新位置。图片由作者提供。
重复计算距离并分配标注。
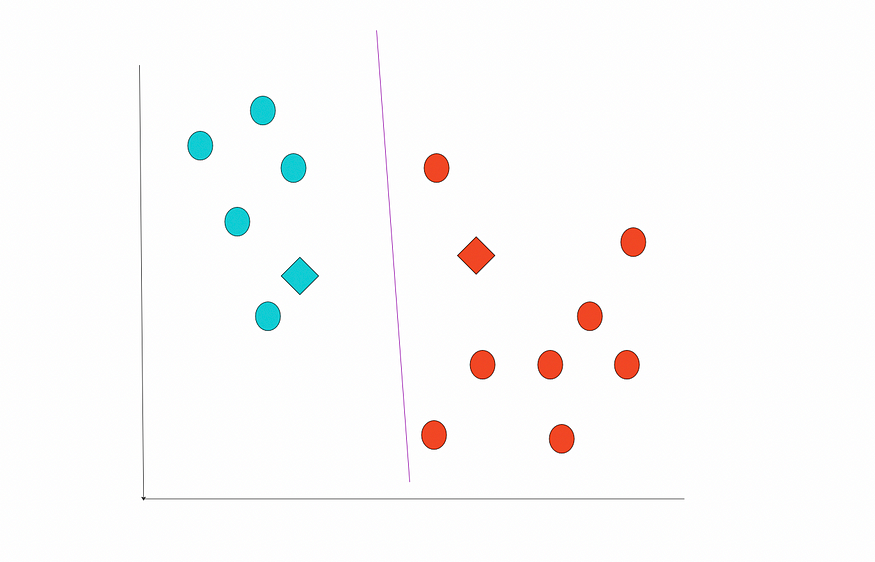
New labels. Image by the author.
Carry the centroids.

携带质心。图片由作者提供。
我们无法再更改位置。这些是最后的集群。
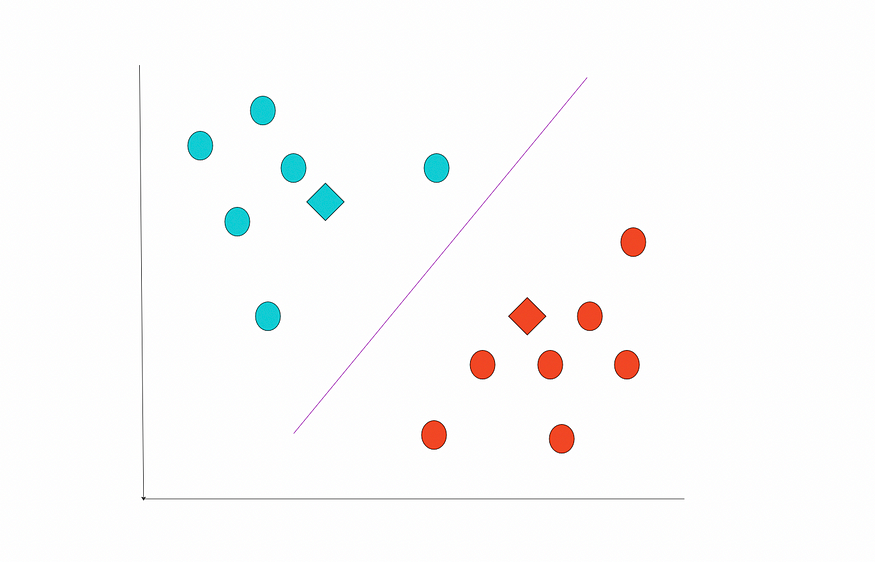
最终状态。图片由作者提供。
三、算法积极的一面
- 简单。易于理解和解释。
- 多才多艺。K-Means 可用于广泛的聚类任务,包括图像分割、文本分类和市场细分。
- 快。它通常提供快速解决方案(当然取决于数据集和问题定义)。
四、约束
- 群集形状。它不适用于具有细长形状或不均匀形状的簇。
- 初始条件。不同的初始条件可以产生不同的最终聚类
- 异常。对异常值敏感。
- 高维数据。对于更高维度的数据效率不高。
五、代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
np.random.seed(42)
# dataset
x1 = np.random.normal(0, 0.5, (50, 2))
x2 = np.random.normal(3, 0.5, (50, 2))
X = np.concatenate([x1, x2], axis=0)
# k-means
model = KMeans(n_clusters=2)
model.fit(X)
labels = model.predict(X)
# plot
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.scatter(model.cluster_centers_[:, 0], model.cluster_centers_[:, 1], marker='x', s=200, linewidths=3, color='r')
plt.show()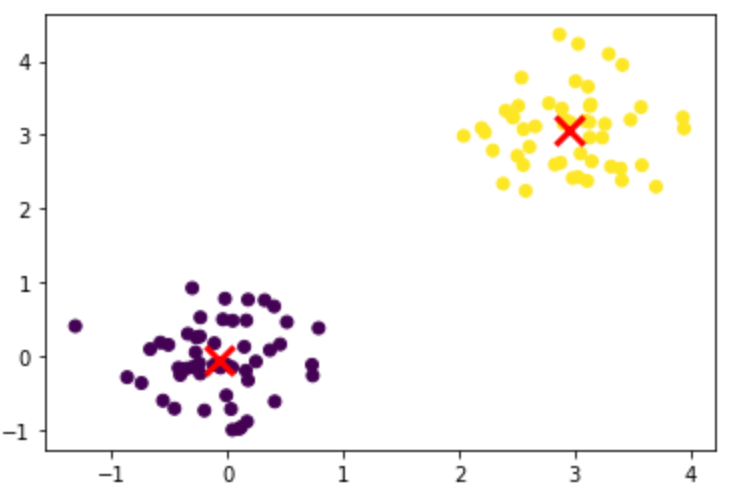
图片由作者提供。
如上所述,K-Means 不适用于不均匀的形状:
from sklearn.datasets import make_moons
# nonuniform shape
X, _ = make_moons(n_samples=200, noise=0.05, random_state=0)
model = KMeans(n_clusters=2)
model.fit(X)
labels = model.predict(X)
# plot
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.scatter(model.cluster_centers_[:, 0], model.cluster_centers_[:, 1], marker='x', s=200, linewidths=3, color='r')
plt.show()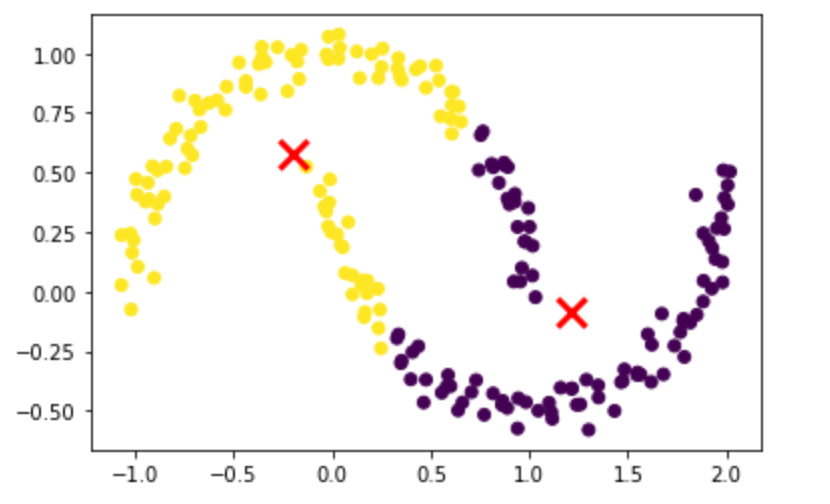
Not a good result. Image by the author.
The parameters of the model of :KMeanssklearn
n_clusters是聚类数。这是最重要的参数。如果我们没有关于要使用的集群数量的先验信息,我们可以使用 elbow 方法(如下所述)。init指定初始化质心的方法。默认方法是 ,它巧妙地选择初始质心以减少收敛所需的迭代量。另一个选项是 ,它随机初始化质心。 通常是首选。"k-means++""random""k-means++"n_init指定使用不同质心种子运行算法的次数。最终结果将是惯性方面连续运行n_init的最佳输出。常见的选择是设置 .如果算法容易卡在局部最小值,则可以使用较高的值。n_init=10max_iter是单次运行的最大迭代次数。300 是一个不错的选择。tol是关于聚类内平方和变化的容差。如果聚类内平方和的变化小于此值,则算法将停止。常见的选择是设置 .tol=1e-04
重要属性:
cluster_centers_包含聚类中心。labels_包含每个点的标签。inertia_表示样本到其最近聚类中心的平方距离之和。
六、elbow 法
如果我们没有关于如何选择聚类数量的先验信息,那么我们使用 elbow 方法。
肘部方法背后的想法是在数据集上运行 K-Means 聚类,以获取不同的 k(聚类数)值,并测量点与其最近聚类中心之间的平方距离 (SSE) 之和。
然后将 SSE 值与聚类数绘制,创建“弯头”形状。在 SSE 开始以较慢的速度减少时选择最佳聚类数。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# dataset with 5 clusters
X, _ = make_blobs(n_samples=500, centers=5, random_state=42)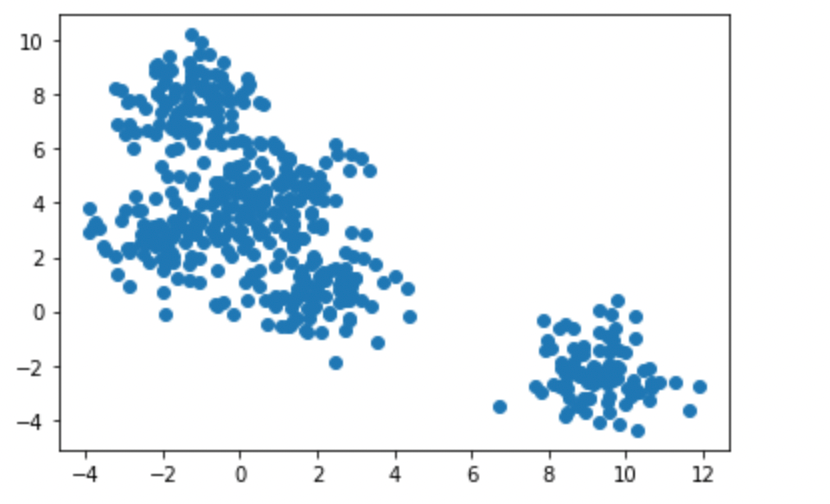
生成的数据集。图片由作者提供。
# the Within-Cluster-Sum of Squared Error (WCSS) for different numbers of clusters
error = []
for i in range(1, 11):
model = KMeans(n_clusters=i, init='k-means++', max_iter=300, n_init=10, random_state=0)
model.fit(X)
error.append(model.inertia_)
# elbow plot
plt.plot(range(1, 11), wcss)
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()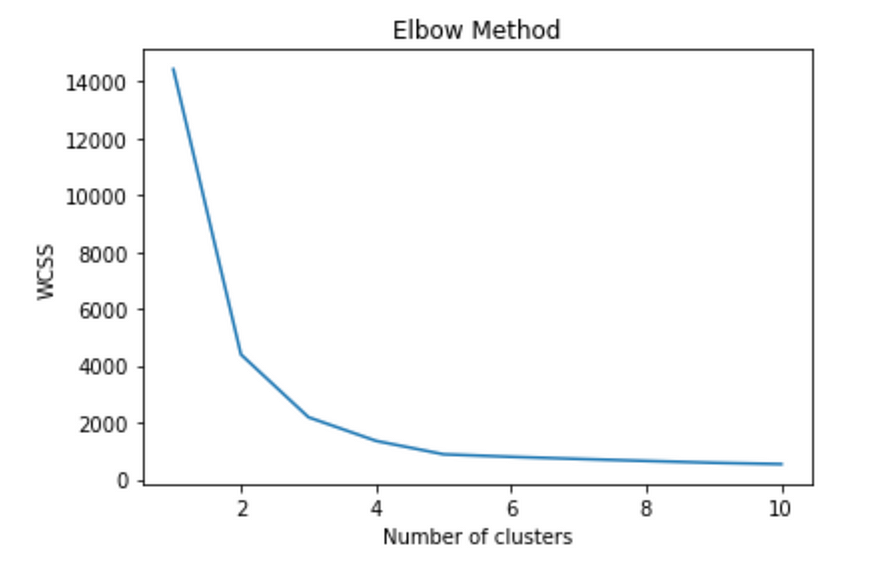
该图显示,WCSS 随着簇数量的增加而减小,并在 5 个簇时达到“肘部”。
# K-Means model with 5 clusters
model = KMeans(n_clusters=5, init='k-means++', max_iter=300, n_init=10, random_state=0)
result = model.fit_predict(X)
# Plot the clusters
plt.scatter(X[:,0], X[:,1], c=result)
plt.scatter(model.cluster_centers_[:, 0], model.cluster_centers_[:, 1], s=300, c='red')
plt.show()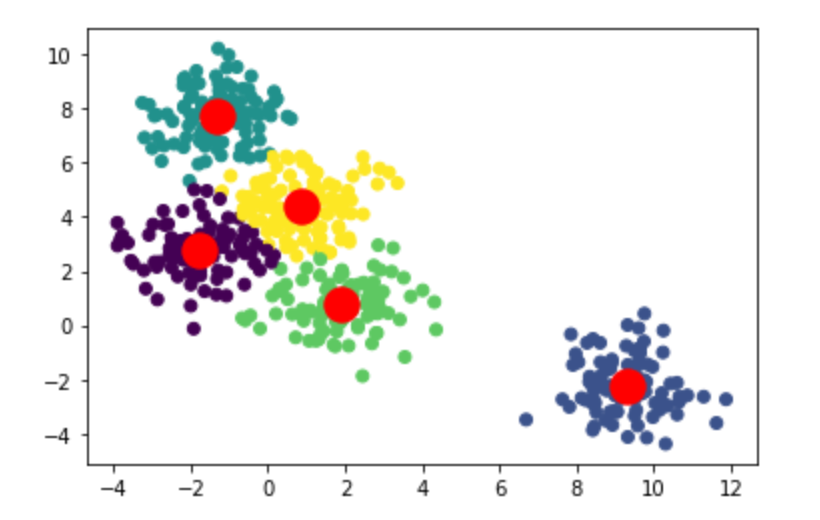
聚类。图片由作者提供。
总之,K-Means聚类是一种广泛使用的无监督机器学习技术,可将相似的数据点分组到聚类中。奥坎·耶尼根