微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

大多数通信系统都是窄带带通型的,通过窄带系统的信号或噪声必然是窄带随机过程
1、窄带随机过程定义
若随机过程ξ(t)的谱密度集中在中心频率fc附近相对窄的频带范围△f内,满足△f≤fc条件,且fc远离零频率,则称ξ(t)为窄带随机过程
2、窄带随机过程的频谱密度和波形
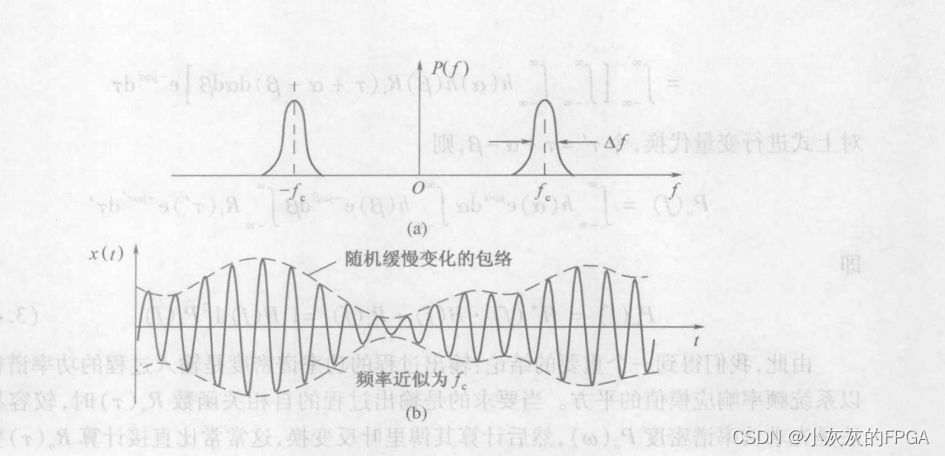
3、窄带随机过程的一个样本的波形如同一个包络和相位随机缓变的正弦波,公式可表示为:
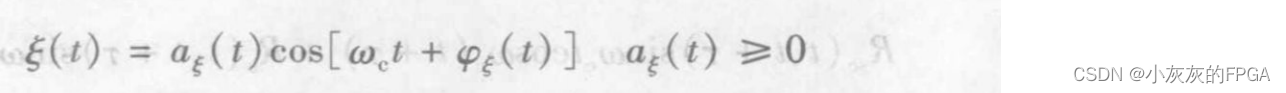
其中aξ(t)为窄带随机过程ξ(t)的随机包络,ψξ(t)为窄带随机过程ξ(t)的随机相位;ωc为正弦波的中心角频率
三角函数展开cos可得
ξ(t)=aξ(t)[cos(ωct)cos(ψξ(t))-sin(ωct)sin(ψξ(t))]
ξ(t)=aξ(t)cos(ψξ(t))cos(ωct)-aξ(t)sin(ψξ(t))sin(ωct)
故可得到
ξ(t)=ξc(t)cos(ωct)-ξs(t)sin(ωct);
ξc(t)=aξ(t)cos(ψξ(t));ξc(t)为ξ(t)的同相分量
ξs(t)=aξ(t)sin(ψξ(t));ξs(t)为ξ(t)的正交分量
4、ξc(t)和ξs(t)的统计特性
结论一:一个均值为零的窄带平稳高斯过程ξ(t),它的同相分量ξc(t)和正交分量ξs(t)也是平稳高斯随机过程,且均值为0,方差也相同
在同一时刻上得到的ξc和ξs是互不相关或独立统计的(因为是高斯过程)。

5、aξ(t)和ψξ(t)的统计特性
结论二:一个均值为零,方差为σ(ξ)^2的窄带平稳高斯过程ξ(t),其包络aξ(t)的一维分布是锐利分布;相位ψξ(t)的一维分布是均匀分布
aξ(t)和ψξ(t)的一维分布是统计独立

通信原理板块——窄带随机过程
news2026/2/12 22:55:11
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/978923.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【web开发】1、flask入门和html开发
文章目录 一、前端三剑客是什么?二、快速开发网站1.安装flask2.根目录下创建templates目录及web.py文件 三、HTML3.1常用标签3.2列表标签3.3表格标签3.4INPUT系列(7个)3.5下拉框3.6多行文本3.7案例:用户注册页面 一、前端三剑客是…
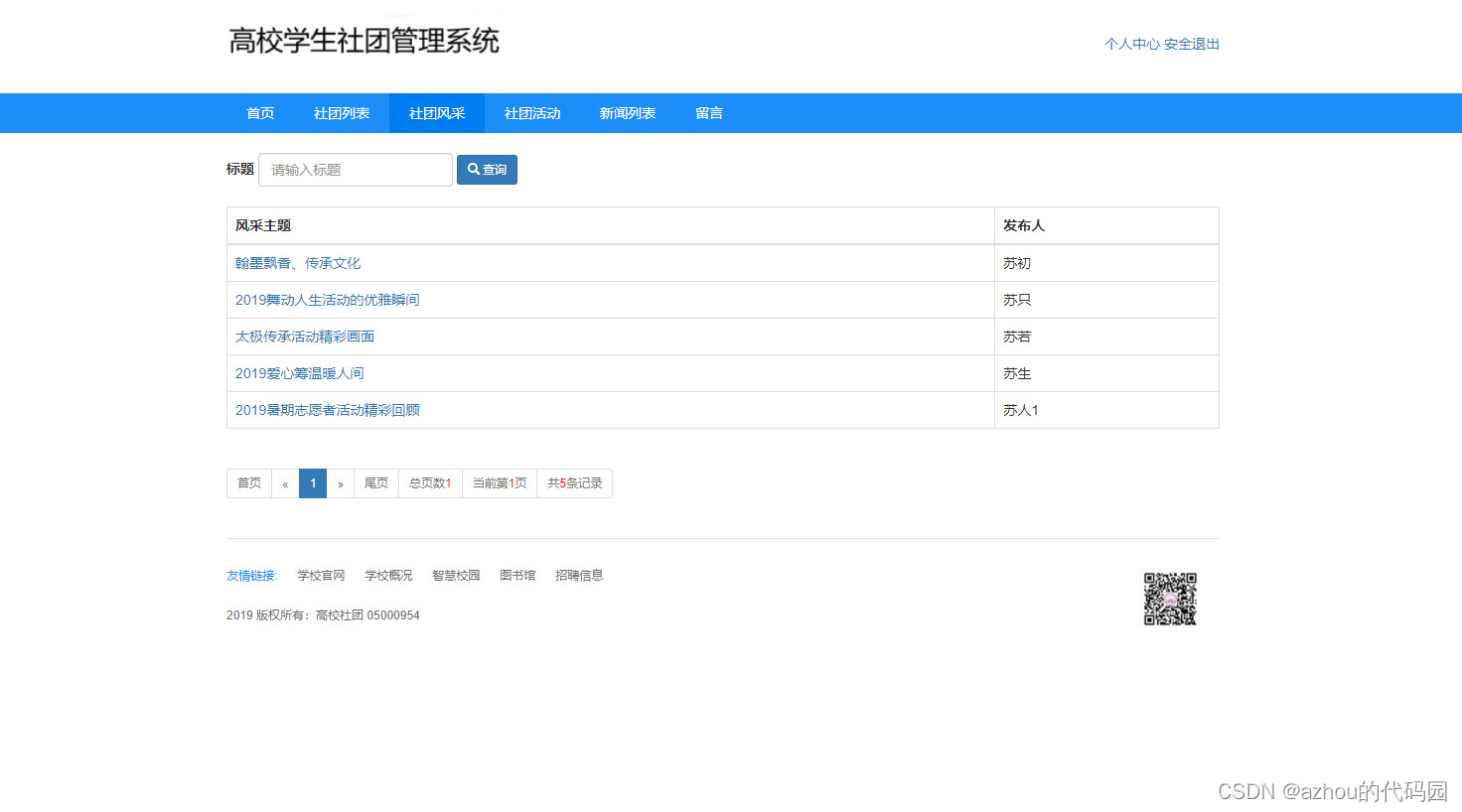
基于SSM的高校社团管理系统
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 随着高校社团数量的不…
Unity中神秘的Transform和transform(小写)的关系
1.为什么Transform类是保护的不能通过new 来实例化对象,也没有静态函数,而Rotate()这种方法却属于它,该如何访问?
Transform 类还是被保护的不允许用户修改! protected Transform(); 是一个受保护的构造函数,不能直接实例化 Transform 类。 2.为甚么transform可以访问Tr…
解决Spring Boot启动错误的技术指南
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…
Java“牵手”微店商品详情数据,微店商品详情API接口,微店API接口申请指南
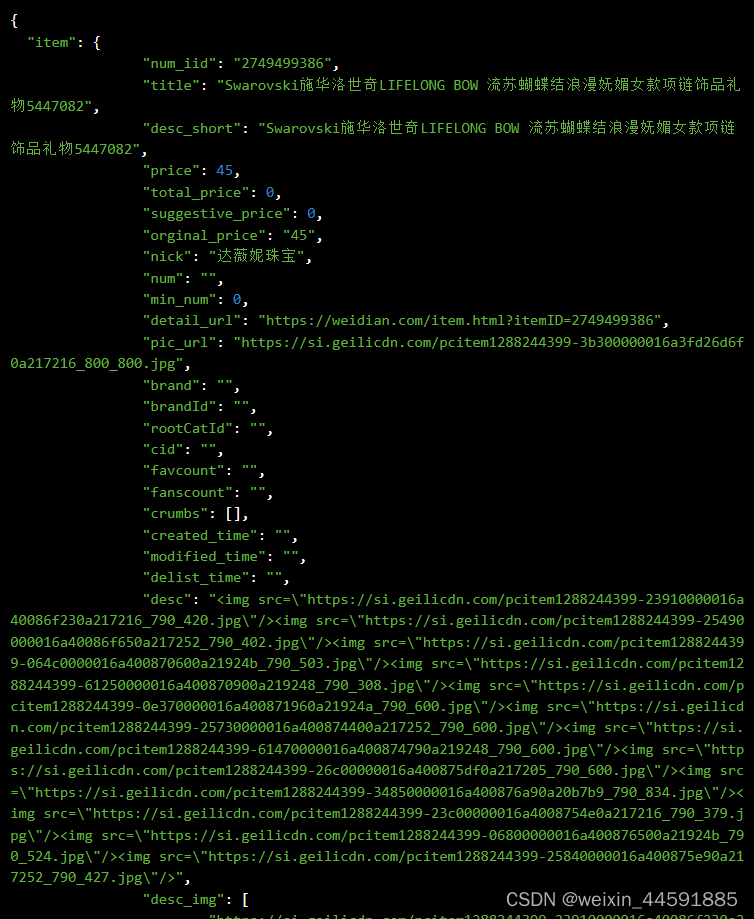
微店平台商品详情接口是开放平台提供的一种API接口,通过调用API接口,开发者可以获取微店商品的标题、价格、库存、月销量、总销量、库存、详情描述、图片等详细信息 。
获取商品详情接口API是一种用于获取电商平台上商品详情数据的接口,通过…
element-ui 修改tooltip样式
1.表格tooltip 统一修改
<el-table:data"tableDatas"tooltip-effect"light"
.el-tooltip__popper.is-light {background: #FFF;box-shadow: 0px 0px 8px 1px rgba(0,0,0,0.16);border-radius: 4px;opacity: 1;border: none;&[x-placement^top] .p…
选择企业网盘:MCN机构如何做出明智的选择?
随着在线媒体行业的迅速发展,MCN机构扮演了越来越重要的角色。对于MCN机构来说,高效的文件管理和协作工具是必不可少的。而企业网盘正是满足这些需求的理想解决方案。 "MCN机构用什么企业网盘好?推荐国际云盘Zoho WorkDive和国内云盘百度…
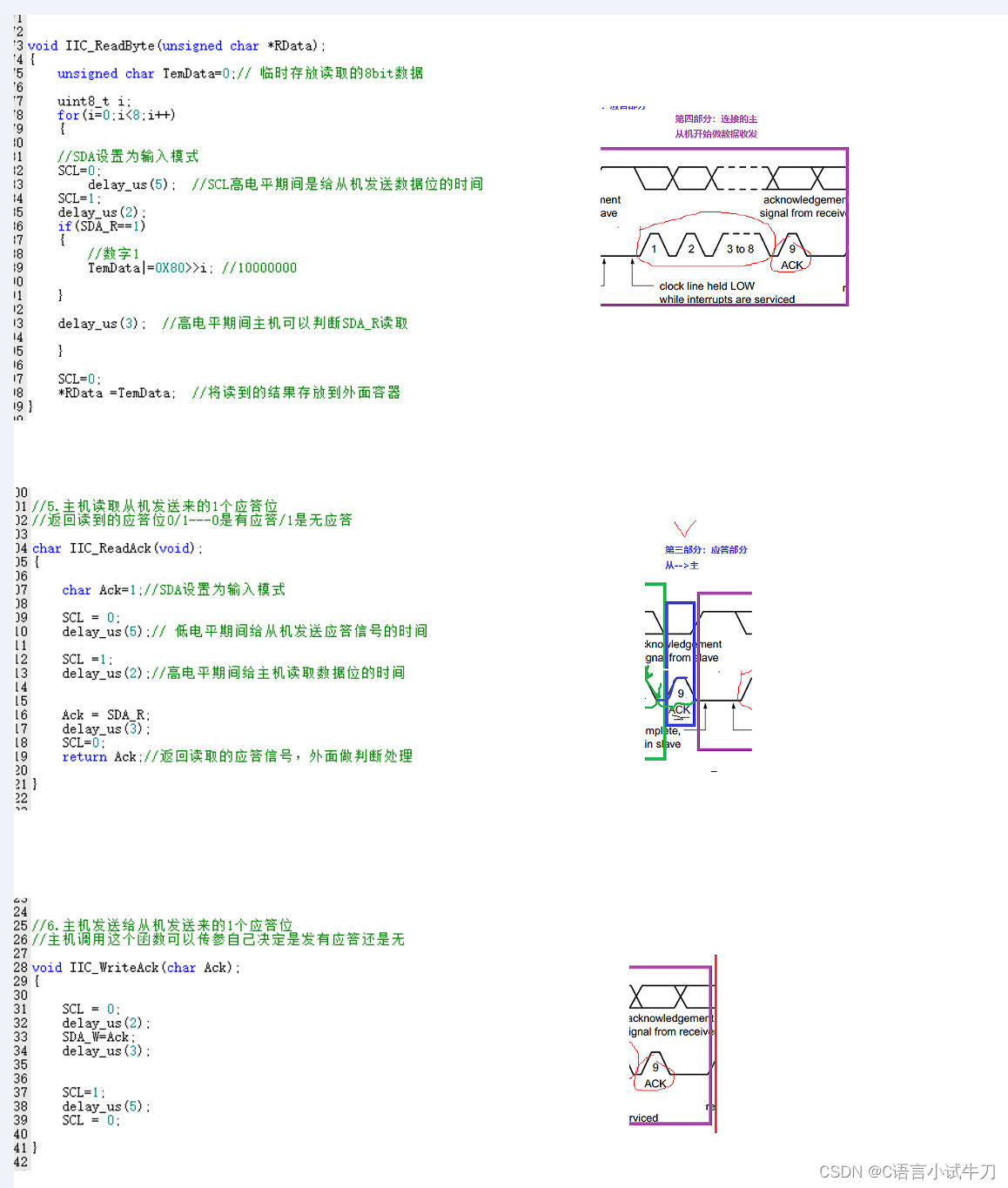
stm32之31.iic
iic双线制。一根是SCL,作为时钟同步线;一根是SDA,作为数据传输线 SDN #include "iic.h"#define SCL PBout(8)#define SDA_W PBout(9)
#define SDA_R PBin(9)void IIC_GPIOInit(void)
{GPIO_InitTypeDef GPIO_InitStructure;//使能时钟GR…
短信软件平台搭建最新客户端|移讯云短信系统
根据客户 和市场需要 增加了新的客户端
新的客户端客户登录后发送短信时可自行选择用哪个通道来进行发送短信。每个通道的充值数量不一样。
通过后台给客户分配可使用的通道,只有在后台给客户分配可使用的通道后客户在登录客户端发送短信时才可进行选择。
关于客…
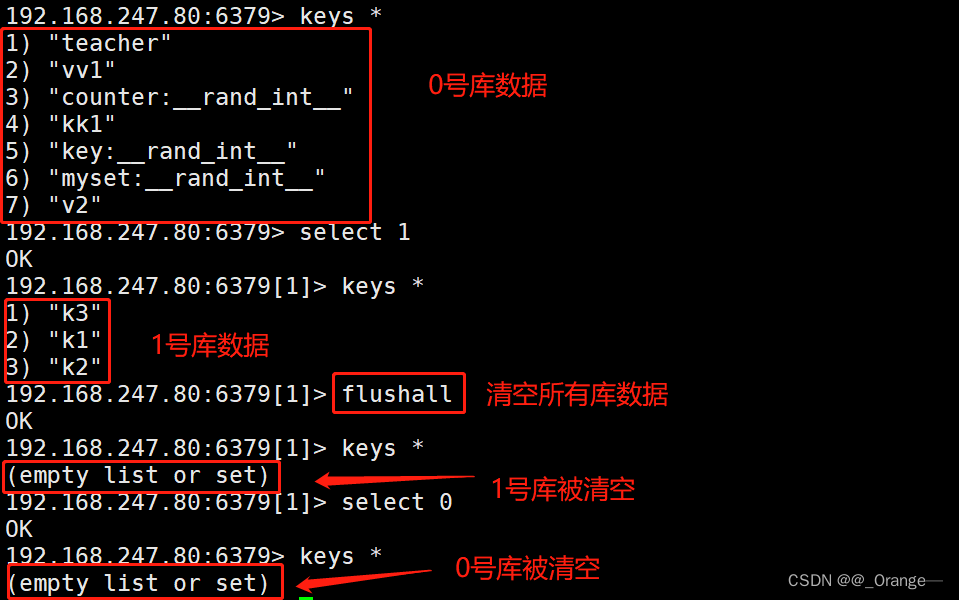
NoSQL之 Redis介绍与配置
目录
一、关系数据库和非关系数据库概述
1、关系型数据库
2、非关系型数据库
二、关系数据库和非关系数据库的区别
1、数据存储格式不同
2、扩展方式不同
3、对事务的支持不同
三、非关系数据库产生背景
1、总结
四、Redis简介
1、 Redis的单线程模式
2、Redis优点…
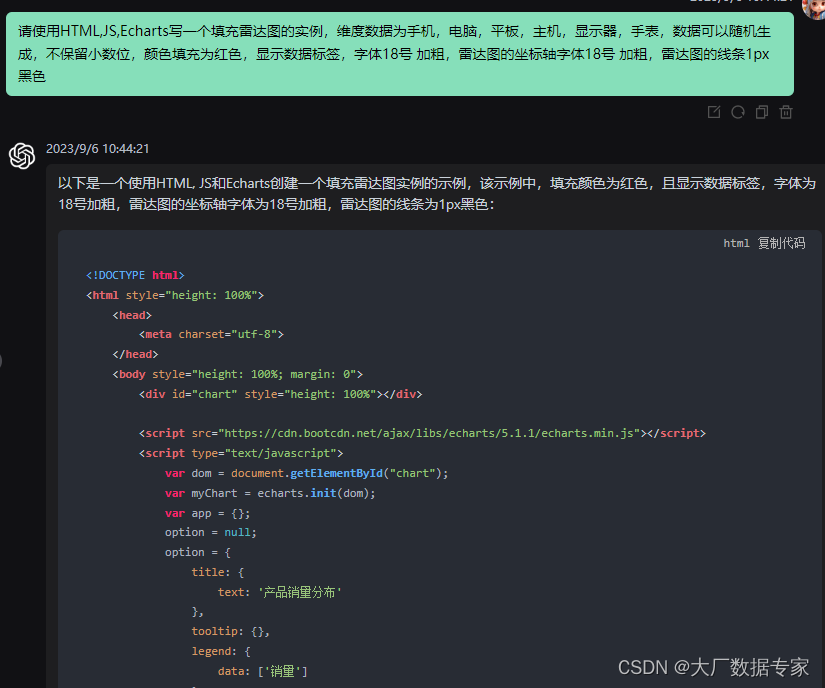
ChatGPT AIGC 完成多维分析雷达图
我们先让ChatGPT来帮我们总结一下多维分析雷达图的功能与作用。 同样ChatGPT AIGC完成的动态雷达图效果如下; 这样的一个多维分析动态雷达图是用HTML,JS,Echarts 来完成的。 将完整代码复制如下:
<!DOCTYPE html>
<html style="height: 100%"><h…
服务性能监控:USE 方法(The USE Method)
USE Method: Rosetta Stone of Performance Checklists
USE Method: Rosetta Stone of Performance Checklists
USE 方法基于 31 模型(三种指标类型一种策略),来切入一个复杂的系统。我发现它仅仅发挥了 5% 的力量,就解决了大概…
基于视觉重定位的室内AR导航项目思路(2):改进的建图和定位分离的项目思路
文章目录 一、建图二、定位首先是第一种方法:几何方法其次是第二种方法:图像检索方法最后是第三种方法:深度学习方法 前情提要:
是第一次做项目的小白,文章内的资料介绍如有错误,请多包含! 一、…
Unity RawImage
文章目录 1. Image2. RawImage2.1 UV Rect 3. RawImage 应用 1. Image
Image 控件在我的这篇博客中有详细解释: https://blog.csdn.net/weixin_45136016/article/details/125655214
2. RawImage
RawImage 组件是一个用来显示纹理的组件,常常跟Render …
【OpenCV入门】第九部分——模板匹配
文章结构 模板匹配方法单模板匹配单目标匹配多目标匹配 多模板匹配 模板匹配方法
模板是被查找的图像。模板匹配是指查找模板在原始图像中的哪个位置的过程。
result cv2.matchTemplate(image, templ, method, mask)image: 原始图像templ: 模板图像&a…
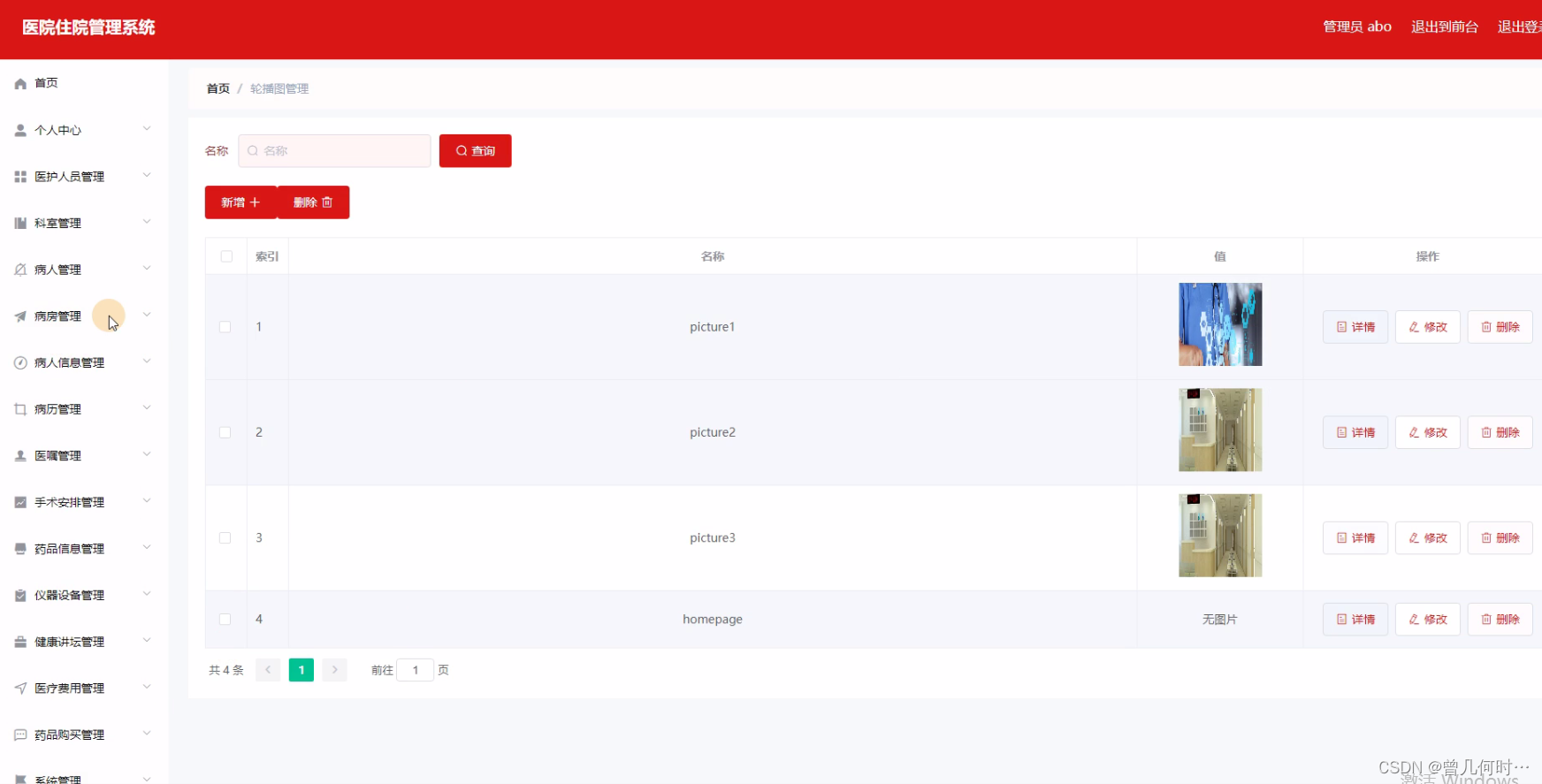
基于SSM的医院住院管理系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用Vue技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…
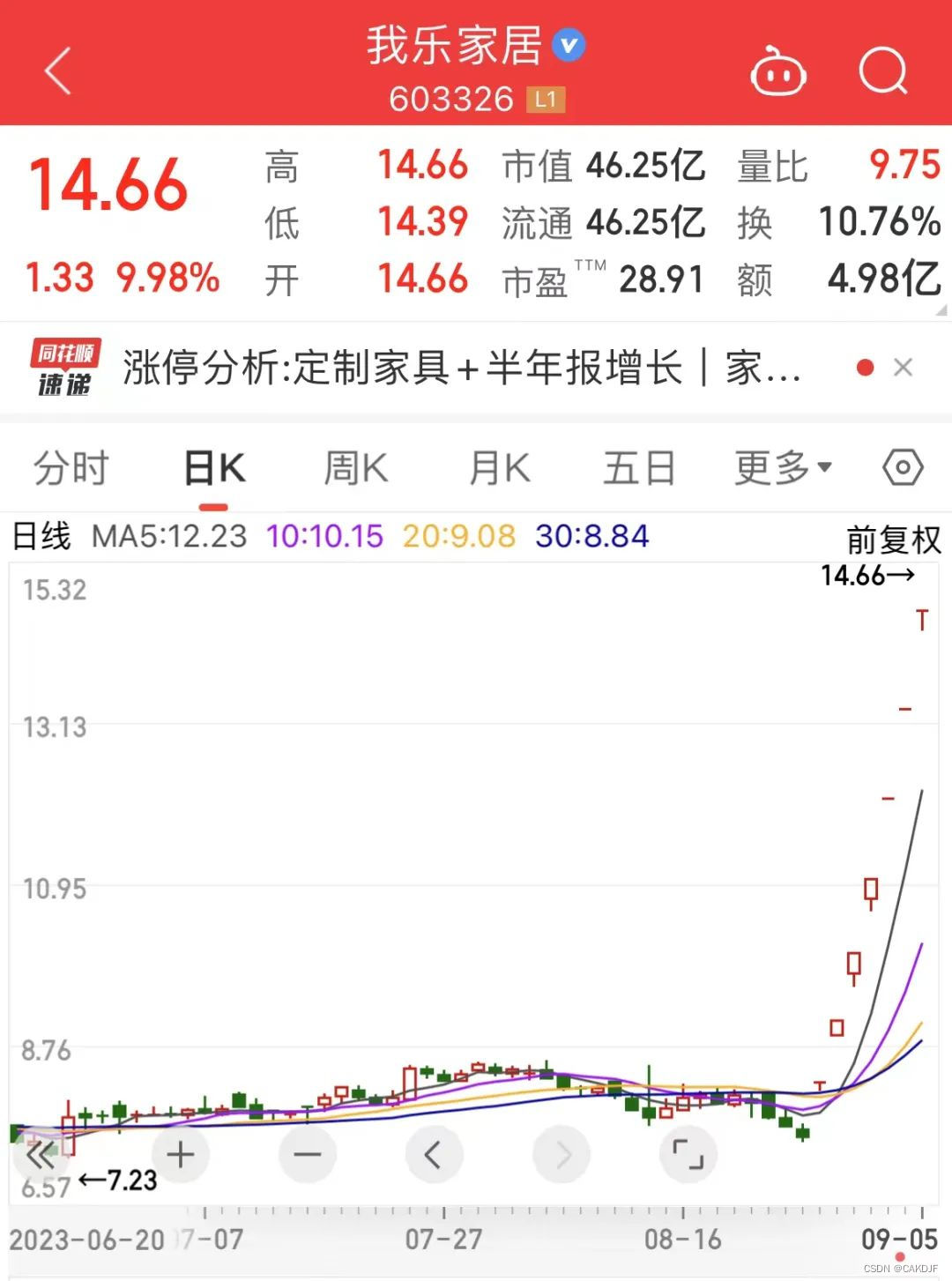
第二证券:放量涨停,牛股狂揽七连板,海外机构扎堆调研股出炉
近10个交易日(8月23日至9月5日),海外组织对343家上市公司进行调研。
昨日,家居人气股我乐家居再获涨停,成功揽获七连板。其全天成交额近4.98亿元,较上一日大幅放量,最新市值为46.25亿元。
昨日…
Spring+MyBatis使用collection标签的两种使用方法
目录 项目场景:
实战操作:
1.创建菜单表
2.创建实体
3.创建Mapper
4.创建xml
属性描述:
效率比较: 项目场景:
本文说明了Spring BootMyBatis使用collection标签的两种使用方法
1. 方法一: 关联查询 2. 方法…