计数排序
- 计数排序
- JAVA实现
- 计数排序优化
- 存在的问题1:
- 存在的问题2
- JAVA实现
- 局限性
冒泡排序,还是快速排序,都是基于元素之间的比较来进行排序
有一些特殊的排序并不基于元素比较,如计数排序、桶排序、基数排序。
计数排序:利用数组下标来确定元素的正确位置的
线性时间排序算法:
- 计数排序
- 桶排序
计数排序
遍历数组,记录每个数字出现的次数

该数组中每一个下标位置的值代表数列中对应整数出现的次数。
最后:直接遍历数组,输出数组元素的下标值,元素的值是几,就输出几次。
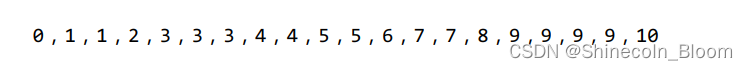
适用范围:它适用于一定范围内的整数排序。在取值范围不是很大的情况下,
JAVA实现
package mysort.countingSort;
import java.util.Arrays;
public class countingSort {
public static int[] countSort(int[] array){
//取数列的最大值
int max = array[0];
for (int i = 1;i<array.length;i++){
if(array[i]>max){
max = array[i];
}
}
//根据数组最大值确定统计数组countArray的长度
//默认条件是:数组元素非负
int[] countArray = new int[max+1];
//遍历数组,统计个数,并填充统计数组countArray
for (int i=0;i<array.length;i++){
countArray[array[i]]++;
}
//遍历统计数组countArray,输出结果
//index是记录sortedArray数组填充到哪的一个下标(每次填充,就加1)
int index = 0;
//创建一个和array一样长度的数组,用于存放最后的输出结果
int[] sortedArray = new int[array.length];
//外层循环是对countArray的每一个位置进行遍历
//内层循环是针对countArray的一个位置,
// 这个位置值是i
// 对应的元素个数是countArray[i]
//把他存入sortedArray
for (int i=0;i<countArray.length;i++){
for (int j=0;j<countArray[i];j++){
sortedArray[index]=i;
index++;
}
}
return sortedArray;
}
public static void main(String[] args) {
int [] array = new int[]{4,4,6,5,3,2,8,1,7,5,6,0,10};
int[] sortarrray = countSort(array);
System.out.println(Arrays.toString(sortarrray));
}
}
计数排序优化
存在的问题1:
我们只以数列的最大值来决定统计数组的长度,其实并不严谨。
解决方案:只要不再以输入数列的最大值+1作为统计数组的长度,而是以数列最大值-最小值+1作为统计数组的长度即可。
数列的最小值作为一个偏移量,用于计算整数在统计数组中的下标。
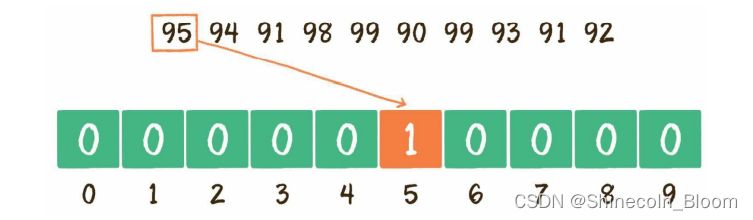
数组的长度为99-90+1=10
第1个整数95,对应的统计数组下标是95-90 = 5
存在的问题2
给出一个学生成绩表,要求按成绩从低到高进行排序,如果成绩相同,则遵循原表固有顺序。
注意:这里的重点条件是:如果成绩相同,则遵循原表固有顺序。

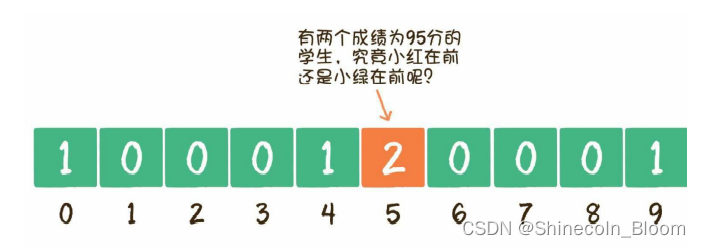
将统计数组变形为:
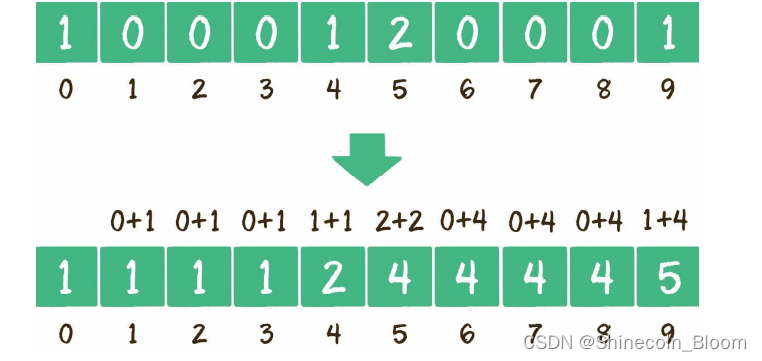
变形规则是:从统计数组的第2个元素开始,每一个元素都加上前面所有元素之和。
这样相加的目的,是让统计数组存储的元素值,等于相应整数的最终排序位置的序号。
第1步,遍历成绩表最后一行的小绿同学的成绩。
小绿的成绩是95分,找到countArray下标是5的元素,值是4,代表小绿的成绩排名位置在第4位。
同时,给countArray下标是5的元素值减1,从4变成3,代表下次再遇到95分的成绩时,最终排名是第3。(小红就是第三位)
这样就达到了:如果成绩相同,则遵循原表固有顺序的目的。

这样一来,同样是95分的小红和小绿就能够清楚地排出顺序了,也正因为此,优化版本的计数排序属于稳定排序。
JAVA实现
package mysort.countingSort;
import java.util.Arrays;
public class countingSort2 {
public static int[] countSort(int[] array){
//1.得到数列的最大值和最小值,并算出差值d
int max = array[0];
int min = array[0];
for (int i = 1;i<array.length;i++){
if(array[i]>max){
max= array[i];
}
if(array[i]<min){
min = array[i];
}
}
//利用这插值确定需要构建的数组长度
int d = max-min;
//2.创建统计数组
int[] countArray = new int[d+1];
//3统计对应元素的个数 (array[i]-min就是array数组中元素的偏移地址)
for (int i=0;i<array.length;i++){
countArray[array[i]-min]++;
}
System.out.println("原始的计数数组为"+Arrays.toString(countArray));
//统计数组做变形,后面的元素等于前面的元素之和
for (int i =1;i<countArray.length;i++){
countArray[i]+=countArray[i-1];
}
System.out.println("变形后的计数数组为"+Arrays.toString(countArray));
//4.倒序遍历原始数列,从统计数组找到正确位置,输出到结果数组
//countArray[array[i]-min]-1其中减去1的原因是在sortedArray数组中,下标从0开始。。
//就以95小绿为例子
int[]sortedArray = new int[array.length];
for (int i=array.length-1;i>=0;i--){
sortedArray[countArray[array[i]-min]-1]=array[i];
//在将countArray中存储的数字(位置)减去1
countArray[array[i]-min]--;
}
return sortedArray;
}
public static void main(String[] args) {
int [] array = new int[]{90,99,95,94,95};
int[] sortedArray = countSort(array);
System.out.println(Arrays.toString(sortedArray));
}
}

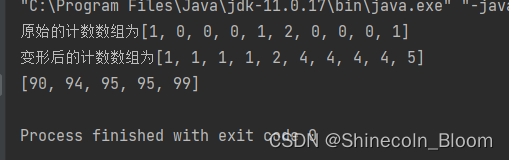
时间复杂度:O(n+m)。代码第1、2、4步都涉及遍历原始数列,运算量都是n,第3步遍历统计数列,运算量是m,所以总体运算量是3n+m ,用大O表示法得去掉系数。
空间复杂度:只考虑统计数组大小的话,空间复杂度是O(m)。
局限性
- 当数列最大和最小值差距过大时,并不适合用计数排序。
- 当数列元素不是整数时,也不适合用计数排序。
解决方案:桶排序




![[C语言数据结构]万字长文带你学习八大排序](https://img-blog.csdnimg.cn/0511318ab1e94d548bed34a4335ece19.gif#pic_center)