第一节

主成分的计算步骤:1、主成分建模,标准化处理。2、计算特征根、特征向量。3、选取主成分个数。
题目

选择B,依次递减。

相关系数和关联矩阵都做了标准化,做完标准化后方差就不会造成影响,所以选A。

A可以进行判断,虽然没讲过但是可以。BC是正常概念。D没说过。

主成分就是一种降维方法,将本来可能相关的变量转化为不相关的变量。所以选D

变量之间的相关性;行和列没啥关系,行变量关系是聚类了。

高度相关,本来主成分分析就是将相关转为不相关。

A是因子分析,它寻找的是公共因子和特殊因子。B应该是最大方向。C保留K个主成分是对的,但是主成分的特征根是单个就要大于1了。

主成分之间不相关。
如果X与Y是统计独立的,那么二者之间的协方差就是0,因为两个独立的随机变量满足E[XY]=E[X]E[Y]。
但是,反过来并不成立。即如果X与Y的协方差为0,二者并不一定是统计独立的。

A,记。

C
 ABC记;D错
ABC记;D错

答案是B,AC好理解,D记。

正交旋转是因子分析做的。BC;特征值分解=奇异值分解。

ABC;主成分分析不能用于数据分类。
第二节

主成分分析是组合的过程,因子分析是分解的过程。
因子旋转分为正交旋转和斜交旋转。
题目

变量越相关,kmo越大,取值在0到1之间。D

D。因子分析应该是把变量表示成因子的线性组合;因子由变量表示,题目反过来了,成了主成分分析。

C,主成分和因子分析都需要做标准化。

主成分--因子旋转--公共因子。C

B

D

A,做降维肯定小于变量个数。
第三节

题目

模型的表现与变量是非递减,反正要么不变要么增。但是测试集的变化都有可能。

D,逻辑回归是极大似然的对数。

直接写回归一般指定线性回归。
回归问题比分类分类问题复杂。有监督学习是有y的,无监督是没y的。回归问题使用R方;分类问题才用混淆矩阵和ROC曲线。

提示,如果在回归前面不加逻辑回归就指线性回归。多元回归指线性回归。
D

逻辑回归可以是连续变量。B
线性回归Y是连续变量,逻辑回归y是分类变量。
肯定能解决多重共线性,不然模型不稳定。

A
输出的y是logit,因此在计算得y后,还要进行逻辑回归的计算:概率p=1/(1+exp(-logit))。

A

ABC,y是二分类。
第四节

多重共线性,变量与变量间还存在相关性。
残差平方和是指被解释变量观测值总变差中未被列入模型的解释变量。
R2是指回归平方和占总离差平方和的比重。
线性回归分析的前提假设包括:
- 解释变量之间不完全相关
- 随机项满足正态分布
- 解释变量与随机项不相关
- 随机项序列不相关
题目

方差不能变化。D

拟合程度一定使用R2。B

B

A,极大似然也可以。

A肯定不一样啊,多元和一元不一样,参数过程;参数过程也不太一样。步骤是一样的。复杂度肯定不一样。C

C;n*p;n是样本量,p是个数;阶数是变量的个数。一般k,p是变量个数;n是样本量。

满秩,所有变量肯定都是线性无关!C

D,其他三个都不行。

ACD都可以,选B;

A

A

公式越复杂,越容易过拟合和欠拟合。A

D

BCD都可以,knn是临界聚类,不能解决。

A起码留一个才对;B对;CD都可以。

初设为0;A

ESS是残差平方和。C

B

C;X是解释变量;Y是被解释变量;

C,概念。

概念D。

恒定均值就是一条线。不需要回归。A

C

D,个人理解的自相关,前面变量的数据会给后面的数据造成影响。

B

大于10就不行了,多重共线性很严重。D
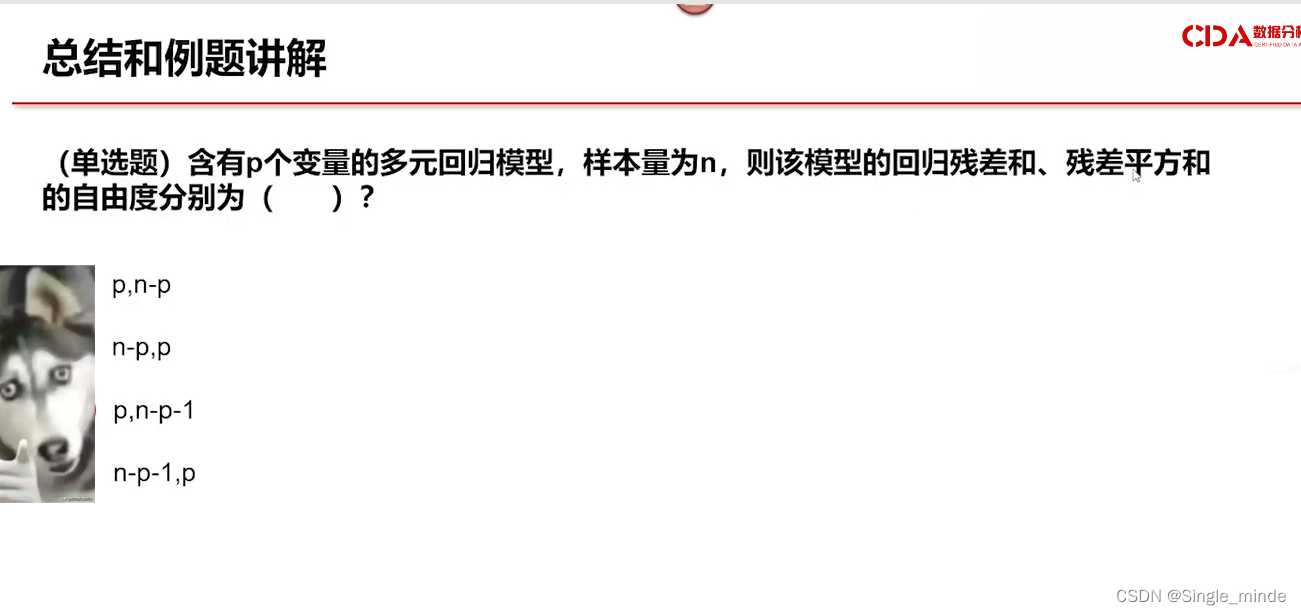
回归残差和的自由度,就是变量的个数。C

加变量,R2肯定变大,本来就是递增的。AD

连续变量不能用众数来补,可以用中位数。ABC

自变量是不可控的,因变量是随机的。比如x是年龄什么的。y是根据x改变的。ACD

ABCD
第五节

聚类的基本逻辑:从n个观察值k个属性开始,对观察值进行两两观察。将相离最近的观测聚为一类,将距离远的分为不同的类。最终达到组间的距离最大化,组内的距离最小化。
系统聚类:可以帮助做分类决策,比较直观,但是不适合做大样本数据。
k-means:可以处理大样本,缺点是K不确定,这个超参数需要经验判断。
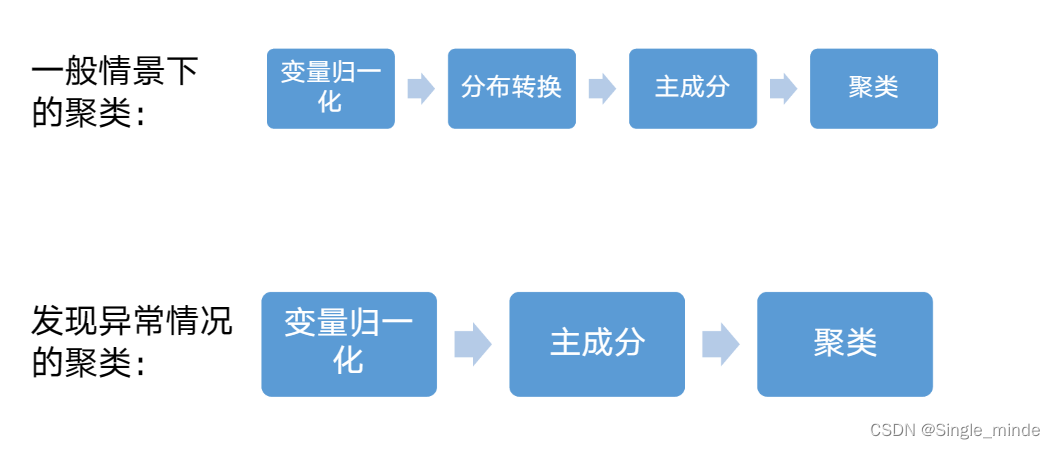
标准化,化为同一单位,尽量相同权值。
需要主成分分析,主要要处理异常值。
K-means聚类过程
- 设定K值,确定聚类数(软件随机分配聚类中心所需的种子):。
- 计算每个记录到类中心的距离(欧式),并分成K类
- 然后把K类中心(均值),作为新的中心,重新计算距离
- 迭代到收敛标准停止(最小二乘准则)
题目

需要进行标准化,统一量纲。需要进行预处理。k不能自动确定。D,要先进行哑变量转换,转成数字。选A

K-means对异常值非常敏感。C

题目说需要建立用户画像,所有要用聚类算法。如果题目说是为了用户留存之类的,要用回归,那么就用逻辑回归。

C

肯定要做标准化,主成分分析可实现降维,有用,但是因子分析涵盖了前面AB,所有选C

聚类是无监督,分类是有监督。
C

D,会把最近的一个点。

D

AB

组间的距离最大化,组内的距离最小化。AD

AB
第六节

winter模型用于趋势成分和季节成分序列的预测。holt模型用于对线性趋势预测。分解法可用于时间序列同时含趋势、季节、随机变动成分。与winter相似



arma判断:

题目

C

季节变动、循环变动、不规则变动、趋势变动。D

C

A

B

B

C

D。自回归就是自己预测自己,时间序列数据必须有平稳性,如果没有,那么要做差分。关注误差项的累计是MA模型。AR模型是关注自身和上一项的关系,即yt=yt-1.

在衰退0附近时,不超过两倍标准差时,为d阶截尾。A

AC

AC