---

前言

手撕排序算法第四篇：选择排序！
从本篇文章开始，我会介绍并分析常见的几种排序，例如像插入排序，冒泡排序，希尔排序，选择排序，快速排序，堆排序，归并排序等等！
这篇文章我先来给大家手撕一下选择排序！

大家可以点下面的链接去阅读其他的排序算法：
C语言手撕排序算法

---

正文开始！

一、常见的排序算法

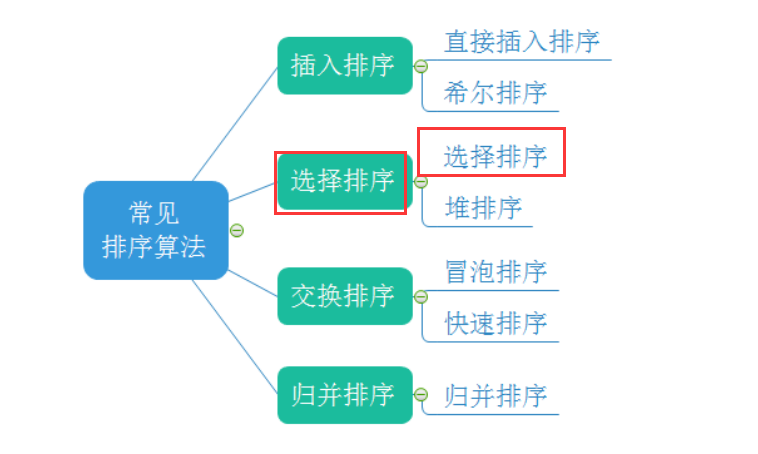
选择排序的基本思想：每一次从待排序的数据元素中选出最小(或最大)的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完！

二、直接选择排序

2.1 单趟排序基本思想

1. 我们遍历一遍数组选出一个最小的数字。
2. 让第一个数字和这个数组进行交换(默认升序)，此时最小的数字就来到了第一个位置。
3. 重复1操作选出第二小的数字，让第二个数字和这个的第二小的数字交换，此时第二小的数字就来到了第二个位置…这样循环选择排序，直到排序完成即可。

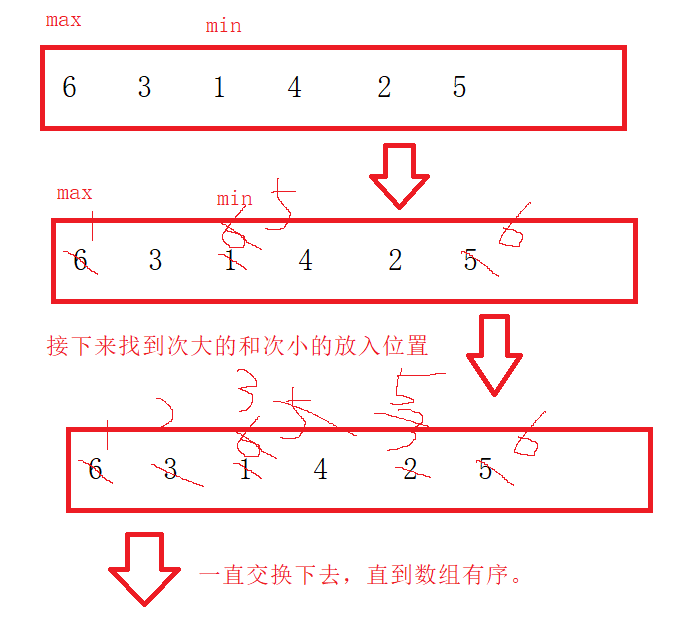
分析图解：

2.2 优化

对于上述方法我们遍历一次数组只找到最小值，没有更好的利用这次。因为既然我们要选择数字，我们不妨选择两个数字。具体步骤如下：

1. 我们遍历一遍数组找到最大值和最小值。
2. 选择完成后让最小值放到第一个位置，让最大值放到最后一个位置。
3. 当左边left<right的时候说明排序已经完成。

代码如下：

void SelectSort(int* a,int n)
{
	int left = 0;
	int right = n - 1;
	while (left < right)
	{
		int mini = left;
		int maxi = left;
		for (int i = left; i <= right;i++)
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
		}
		Swap(&a[left],&a[mini]);
		Swap(&a[right],&a[maxi]);
		left++;
		right--;
	}
}

但是这里有个非常致命的错误，排出来的结果并不是有序的！

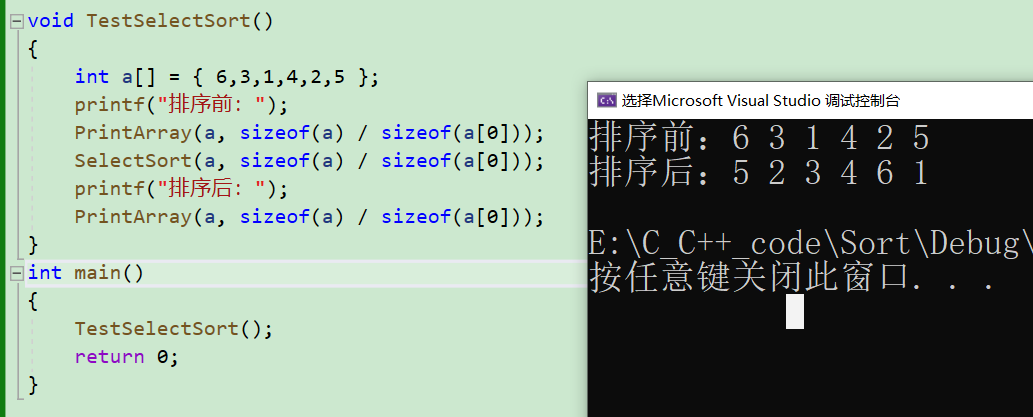
那么这是为什么呢？

所以在第二次进行交换前进行一次判断即可，判断left和maxi的位置时候重叠了，如果重叠了就更新maxi的值。

完善后的代码如下：

void SelectSort(int* a,int n)
{
	int left = 0;
	int right = n - 1;
	while (left < right)
	{
		int mini = left;
		int maxi = left;
		for (int i = left; i <= right;i++)
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
		}
		Swap(&a[left],&a[mini]);
		//如果left和maxi是相等的，修正一下maxi即可。
		if (left == maxi)
		{
			maxi = mini;
		}
		Swap(&a[right],&a[maxi]);
		left++;
		right--;
	}
}
void TestSelectSort()
{
	int a[] = { 6,3,1,4,2,5 };
	printf("排序前：");
	PrintArray(a, sizeof(a) / sizeof(a[0]));
	SelectSort(a, sizeof(a) / sizeof(a[0]));
	printf("排序后：");
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{
	TestSelectSort();
	return 0;
}

三、选择排序测试

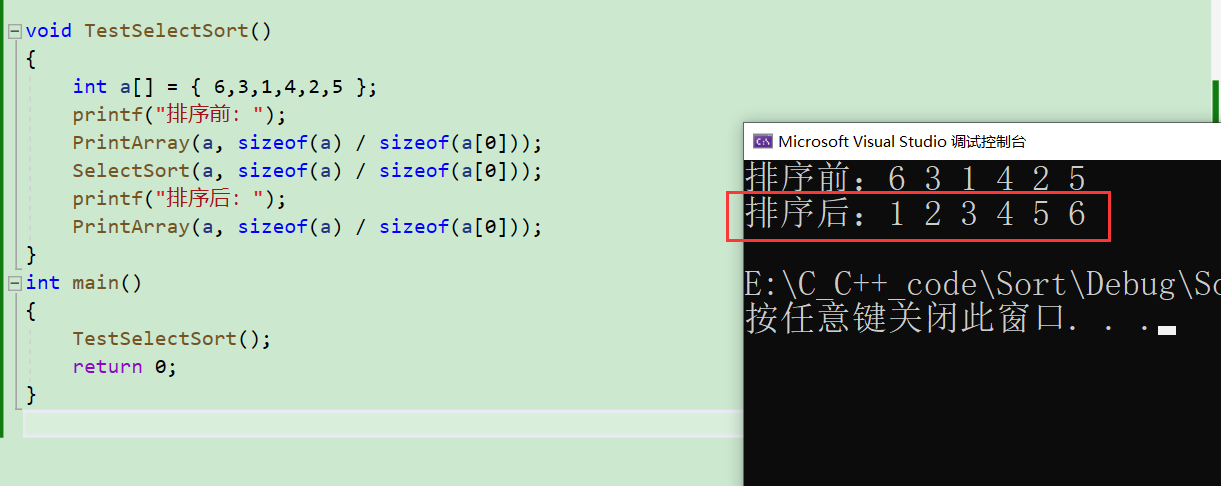
四、选择排序的时间复杂度

选择排序的时间复杂度是O(n^2)。

无论是顺序还是逆序，选择排序的时间复杂度都是O(n^2)。
这是因为在每次遍历数组的时候，都要找出最大和最小的数字，每一次遍历即使O(n)。即使是自身有序的数组，但是计算机不知道，还是要遍历一遍选出最大和最小的。因此综上选择排序的时间复杂度是O(n^2)。

五、直接选择排序的特性

1. 直接选择排序的思想非常好理解，但是效率并不高，实际中很少用到。
2. 时间复杂度O(n^2)。
3. 空间复杂度为O(1)。
4. 稳定性：不稳定。

---

（本章完！）