1. LSTM介绍

长短期记忆网络 LSTM（long short-term memory）是 RNN 的一种变体，其核心概念在于细胞状态以及“门”结构。细胞状态相当于信息传输的路径，让信息能在序列连中传递下去。你可以将其看作网络的“记忆”。理论上讲，细胞状态能够将序列处理过程中的相关信息一直传递下去。因此，即使是较早时间步长的信息也能携带到较后时间步长的细胞中来，这克服了短时记忆的影响。信息的添加和移除我们通过“门”结构来实现，“门”结构在训练过程中会去学习该保存或遗忘哪些信息。LSTM网络介绍

2. 数据集准备及预处理

加载、清理和划分数据集。

DateTime	Temperature	Humidity	Wind Speed	general diffuse flows	diffuse flows	Zone 1 Power Consumption	Zone 2 Power Consumption	Zone 3 Power Consumption
1/1/2017 0:00	6.559	73.8	0.083	0.051	0.119	34055.7	16128.88	20240.96
1/1/2017 0:10	6.414	74.5	0.083	0.07	0.085	29814.68	19375.08	20131.08
1/1/2017 0:20	6.313	74.5	0.08	0.062	0.1	29128.1	19006.69	19668.43
1/1/2017 0:30	6.121	75	0.083	0.091	0.096	28228.86	18361.09	18899.28
1/1/2017 0:40	5.921	75.7	0.081	0.048	0.085	27335.7	17872.34	18442.41
1/1/2017 0:50	5.853	76.9	0.081	0.059	0.108	26624.81	17416.41	18130.12
1/1/2017 1:00	5.641	77.7	0.08	0.048	0.096	25998.99	16993.31	17945.06
1/1/2017 1:10	5.496	78.2	0.085	0.055	0.093	25446.08	16661.4	17459.28
1/1/2017 1:20	5.678	78.1	0.081	0.066	0.141	24777.72	16227.36	17025.54
1/1/2017 1:30	5.491	77.3	0.082	0.062	0.111	24279.49	15939.21	16794.22
1/1/2017 1:40	5.516	77.5	0.081	0.051	0.108	23896.71	15435.87	16638.07

close all
clear
clc
tbl = readtable("国外负荷预测数据集.csv");%读取负荷预测数据
tbl.DateTime = datetime(tbl.DateTime,'InputFormat','dd/MM/yyyy HH:mm');%修改读取时间的格式

tbl = rmmissing(tbl);%数据预处理
head(tbl)
tbl = tbl(:, [1 end-2:end]);%提取3个中心城区负荷消耗数据
head(tbl)
figure
stackedplot(tbl,'XVariable','DateTime')%绘制趋势分布图
title("国外负荷预测数据集")
data = groupSequences(tbl, "DateTime");
[train_data, val_data, test_data] = splitSequence(data);%划分训练测试验证集
muPredictors = mean(cat(2, train_data{:, 1}), 2);
sigmaPredictors = std(cat(2,train_data{:, 1}), 0, 2);

muResponses = mean(cat(2, train_data{:, 2}), 2);
sigmaResponses = std(cat(2, train_data{:, 2}), 0, 2);

for i = 1:size(train_data, 1)
    train_data{i, 1} = (train_data{i, 1} - muPredictors) ./ sigmaPredictors;
    train_data{i, 2} = (train_data{i, 1} - muResponses) ./ sigmaResponses;

    val_data{i, 1} = (val_data{i, 1} - muPredictors) ./ sigmaPredictors;
    val_data{i, 2} = (val_data{i, 1} - muResponses) ./ sigmaResponses;

    test_data{i, 1} = (test_data{i, 1} - muPredictors) ./ sigmaPredictors;
    test_data{i, 2} = (test_data{i, 1} - muResponses) ./ sigmaResponses;
end

groupSequences程序：

function data = groupSequences(tbl, groupByColumn)
arguments
    tbl table
    groupByColumn (1, 1) string
end

if isa(tbl{1, groupByColumn}, "datetime")
    indexes = unique(dateshift(tbl{:, groupByColumn}, "start", "day"), "rows", "stable");
else
    indexes = unique(tbl{:, groupByColumn}, "rows", "stable");
end
indexes = sort(indexes, "ascend");

numIdxs = length(indexes);
data = cell(numIdxs, 1);
if isa(tbl{1, groupByColumn}, "datetime")
    for idx = 1:numIdxs
        data{idx} = tbl{dateshift(tbl{:, groupByColumn}, "start", "day") == indexes(idx), (tbl.Properties.VariableNames ~= groupByColumn)}';
    end
else
    for idx = 1:numIdxs
        data{idx} = tbl{tbl{:, groupByColumn} == indexes(idx), (tbl.Properties.VariableNames ~= groupByColumn)}';
    end
end

end

splitSequence程序：

function [train, val, test] = splitSequence(data, val_perc, test_perc)
arguments
    data (:, 1) cell
    val_perc double = 0.1
    test_perc double = 0.1
end

len = size(data, 1);

train = cell(len, 2);
val = cell(len, 2);
test = cell(len, 2);

for i = 1:len
    steps = size(data{i}, 2);
    stepsTrain = floor((1 - val_perc - test_perc) * steps);
    stepsVal = floor(val_perc * steps);

    train{i, 1} = data{i}(:, 1:stepsTrain-1);
    train{i, 2} = data{i}(:, 2:stepsTrain);
    
    val{i, 1} = data{i}(:, (stepsTrain + 1):(stepsTrain + stepsVal - 1));
    val{i, 2} = data{i}(:, (stepsTrain + 2):(stepsTrain + stepsVal));

    test{i, 1} = data{i}(:, (stepsTrain + stepsVal + 1):(end - 1));
    test{i, 2} = data{i}(:, (stepsTrain + stepsVal + 2):end);
end

end

3. LSTM模型搭建与训练

负荷预测数据集包含3个区域负荷的基础特征。模型搭建：

features = 3;
% Hyperparameters
hidden_units = 256;
max_epochs = 3000;
epoch_drop_period = 30;
batch_size = 32;
grad_thresh = 1;
ilr = 1e-2;%学习率
layers = [
    sequenceInputLayer(features)
    fullyConnectedLayer(hidden_units)
    lstmLayer(hidden_units, "OutputMode", "sequence")
    dropoutLayer(0.5)
    fullyConnectedLayer(features)
    regressionLayer
    ]

模型训练超参数设置：优化器选择带动量的随机梯度下降算法

opts = trainingOptions("sgdm", ...
    "MaxEpochs", max_epochs, ...
    "MiniBatchSize", batch_size, ...
    "ValidationData", {val_data(:, 1), val_data(:, 2)}, ...
    "GradientThreshold", grad_thresh, ...
    "InitialLearnRate", ilr, ...
    "LearnRateSchedule", "piecewise", ...
    "LearnRateDropPeriod", epoch_drop_period, ...
    "Shuffle", "every-epoch", ...
    "Plots", "training-progress", ...
    "Verbose", true ...
    )
net = trainNetwork(train_data(:, 1), train_data(:, 2), layers, opts);

4. 预测模型测试

使用测试数据集进行预测并计算均方根误差（RMSE）。此外，从序列的RMSE绘制直方图，其显示与RMSE矩阵的特定值相对应的误差量。最后，绘制了测试数据集中第一个序列的地面真相和预测，以查看两者之间的差异。

test_preds = predict(net, test_data(:, 1));

rmse = zeros(size(test_preds, 1), 1);
for i = 1:size(test_preds,1)
    rmse(i) = sqrt(mean((test_preds{i} - test_data{i, 2}).^2,"all"));
end
mrmse = mean(rmse);
clear i

figure
histogram(rmse)
xlabel("RMSE")
ylabel("Frequency")
title("Test Mean RMSE := " + num2str(mrmse))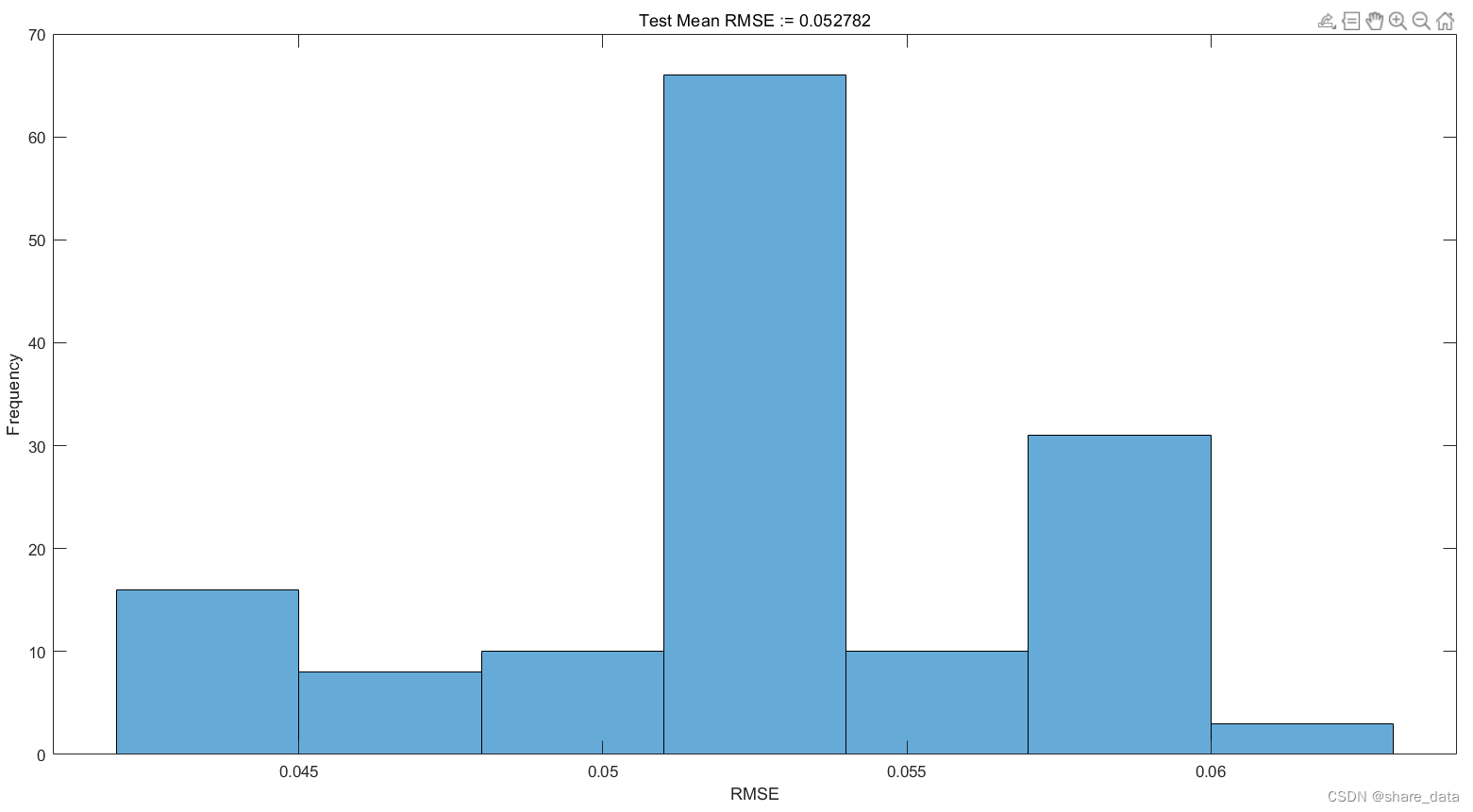

tbl1 = table(test_data{1, 2}(1, :)', test_data{1, 2}(2, :)', test_data{1, 2}(3, :)', 'VariableNames', ["Zone 1", "Zone 2", "Zone 3"]);
tbl2 = table(test_preds{1}(1, :)', test_preds{1}(2, :)', test_preds{1}(3, :)', 'VariableNames', ["Zone 1", "Zone 2", "Zone 3"]);
figure
stackedplot(tbl1)
title( "真实值")
stackedplot(tbl2)
title( "预测值")
save powerConsumptionNet.mat

博客中涉及一些网络资源，如有侵权请联系删除。

该项目实现过程中的不足之处：没有利用天气特征进行负荷预测（后续优化）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/97593.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！