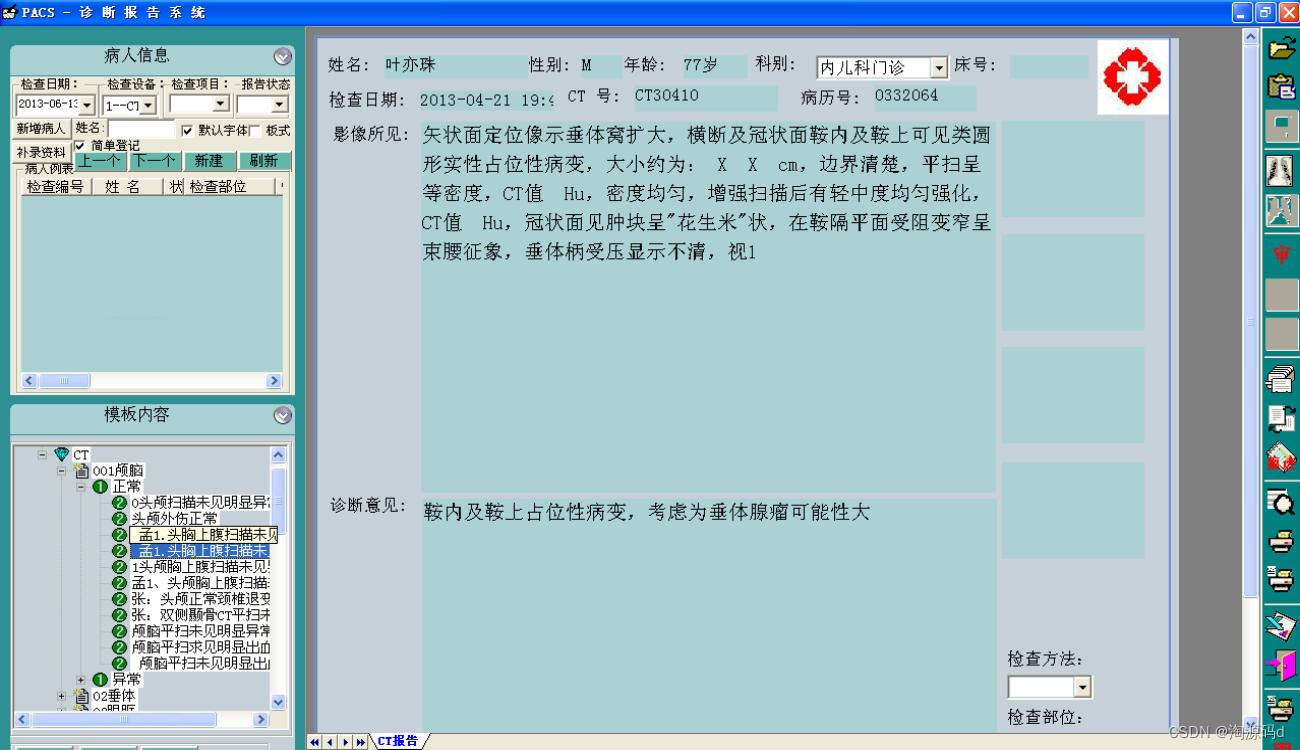
Recently, Kolya found out that a new movie theatre is going to be opened in his city soon, which will show a new movie every day for nn days. So, on the day with the number 1≤i≤n, the movie theatre will show the premiere of the ii-th movie. Also, Kolya found out the schedule of the movies and assigned the entertainment value to each movie, denoted by aiai.
However, the longer Kolya stays without visiting a movie theatre, the larger the decrease in entertainment value of the next movie. That decrease is equivalent to d⋅cntd⋅cnt, where dd is a predetermined value and cntcnt is the number of days since the last visit to the movie theatre. It is also known that Kolya managed to visit another movie theatre a day before the new one opened — the day with the number 0. So if we visit the movie theatre the first time on the day with the number ii, then cntcnt — the number of days since the last visit to the movie theatre will be equal to ii.
For example, if d=2 and a=[3,2,5,4,6], then by visiting movies with indices 1 and 3, cntcnt value for the day 11 will be equal to 1−0=1 and cntcnt value for the day 3 will be 3−1=2, so the total entertainment value of the movies will be a1−d⋅1+a3−d⋅2=3−2⋅1+5−2⋅2=2
Unfortunately, Kolya only has time to visit at most mm movies. Help him create a plan to visit the cinema in such a way that the total entertainment value of all the movies he visits is maximized.
Input
Each test consists of multiple test cases. The first line contains a single integer tt (1≤t≤10^4) — the number of test cases. The description of the test cases follows.
The first line of each test case contains three integers n, m, and d (1≤n≤2⋅10^5, 1≤m≤n 1≤d≤10^9).
The second line of each set of input data contains nn integers a1,a2,…,an (−109≤ai≤10^9) — the entertainment values of the movies.
It is guaranteed that the sum of nn over all test cases does not exceed 2⋅10^5.
Output
For each test case, output a single integer — the maximum total entertainment value that Kolya can get.
题目大意:给定一个长度为n 的数组 n 从中选 不超过 m个数 ai-(i-cnt) 加和最大(cnt初始是0)
输入样例
6
5 2 2
3 2 5 4 6
4 3 2
1 1 1 1
6 6 6
-82 45 1 -77 39 11
5 2 2
3 2 5 4 8
2 1 1
-1 2
6 3 2
-8 8 -2 -1 9 0
输出样例
2
0
60
3
0
7
分析:

假设从小到大选择了k个下标i1,i2,…,ik 此时的结果是
= (ai1−d⋅i1)+(ai2−d⋅(i2−i1))+…+(aik−d⋅(ik−ik−1))(ai1+ai2+…+aik)−d⋅(i1+i2−i1+i3−i2+…+ik−ik−1)= (ai1+ai2+…+aik)−d⋅ik
可以发现结果中减去的部分只取决于最大的下标,因此可以从小到大枚举最后一个下标kk选什么,然后再从前面的下标i∈[1,k−1]中选出最大的m−1个ai(此时已经选择了ak),来使得结果最大。因此可以开个堆来维护前缀的前m−1m−1个最大值以及他们的和。需要注意的是,如果ak≤0那么我们永远不会选择这个元素,从上面的式子可以看出,如果kk不作为最大的下标,那么我们将ak删除结果不会变小,而如果k作为最大的下标,那么删除ak且d⋅ik变小,结果会变小。总之删除ak结果一定不会变小。
时间复杂度为O(nlogm)
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#define int long long
using namespace std;
signed main()
{
int t;
cin>>t;
while(t--)
{
int n,m,d;cin>>n>>m>>d;
int sum=0;
int max1=0;
priority_queue<int,vector<int>,greater<int>>q;
for(int i=1;i<=n;i++)
{
int x;cin>>x;
if(x>0)
{
if(q.size()<m)
{
q.push(x);
sum+=x;
}
else if(q.top()<x)
{
sum-=q.top();
q.pop();
q.push(x);
sum+=x;
}
}
max1=max(max1,sum-i*d);
}
cout<<max1<<endl;
}
return 0;
}